Zero

Zero este un număr întreg notat cu 0 care, atunci când este utilizat ca număr de numărare, înseamnă că nu există obiecte. Este singurul număr întreg (și, de fapt, singurul număr real) care nu este nici negativ, nici pozitiv. Un număr care nu este zero se spune că este diferit de zero. O rădăcină a unei funcții este, de asemenea, cunoscută uneori ca „un zero al lui .”

Segmentul Schoolhouse Rock „My Hero, Zero” (Eroul meu, Zero) preamărește virtuțile lui zero cu laude precum: „Eroul meu, zero Un erou atât de mic și amuzant Dar până să apari tu Ne-am numărat pe degete de la mâini și de la picioare Acum ești aici pentru a rămâne Și nimeni nu știe cu adevărat Cât de minunat ești De ce nu am putea ajunge niciodată la o stea Fără tine, zero, eroul meu Cât de minunat ești.”

Se consideră în mod obișnuit că zero are factorizarea (de ex, în comanda FactorInteger a limbajului Wolfram). Pe de altă parte, divizorii și funcția de divizor sunt în general luate ca fiind nedefinite, deoarece, prin convenție, (adică împarte 0) pentru fiecare cu excepția lui zero.

Pentru că numărul de permutări ale elementelor 0 este 1, (factorialul zero) este definit ca fiind 1 (Wells 1986, p. 31). Această definiție este utilă în exprimarea multor identități matematice într-o formă simplă.

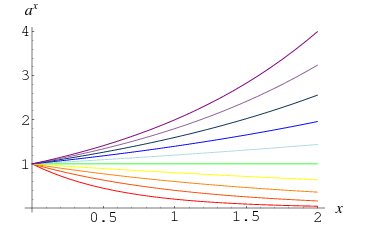
Un număr diferit de 0 dus la puterea 0 este definit ca fiind 1, ceea ce rezultă din limita

Acest fapt este ilustrat de convergența curbelor la în graficul de mai sus, care arată pentru , 0.4, …, 2.0. De asemenea, poate fi văzut mai intuitiv observând că dacă se ia în mod repetat rădăcina pătrată a unui număr se obțin numere din ce în ce mai mici care se apropie de unu de sus, în timp ce dacă se face același lucru cu un număr între 0 și 1 se obțin numere din ce în ce mai mari care se apropie de unu de jos. Pentru rădăcini pătrate, puterea totală luată este , care se apropie de 0 pe măsură ce este mare, dând în limita în care este mare.

însuși este nedefinit. Lipsa unei semnificații bine definite pentru această cantitate rezultă din faptele reciproc contradictorii că este întotdeauna 1, deci ar trebui să fie egal cu 1, dar este întotdeauna 0 (pentru ), deci ar trebui să fie egal cu 0. S-ar putea argumenta că este o definiție naturală, deoarece

Cu toate acestea, limita nu există pentru valorile complexe generale ale lui . Prin urmare, alegerea definiției pentru este de obicei definită ca fiind nedeterminată.

Cu toate acestea, definirea lui permite ca unele formule să fie exprimate simplu (Knuth 1992; Knuth 1997, p. 57), dintre care un exemplu este frumoasa formulă analitică pentru integrala funcției sinc generalizate

dată de Kogan (cf. Espinosa și Moll 2000), unde , , iar este funcția podea.

Teorema lui Richardson este un rezultat fundamental în teoria decidabilității care stabilește că determinarea faptului dacă chiar și expresiile simple sunt identic egale cu zero este nedecisibilă în principiu, darămite în practică.

Tabelul următor oferă primele câteva numere astfel încât expansiunea zecimală a lui să nu conțină zerouri pentru mici (o problemă care seamănă cu întrebarea lui Gelfand.) Cel mai mare cunoscut pentru care nu conține zerouri este 86 (Madachy 1979), fără alte (M. Cook, com. pers.., 26 sept. 1997 și 16 mart. 1998), îmbunătățind limita obținută de Beeler și Gosper (1972). Valorile astfel încât pozițiile celui mai din dreapta zero din crește sunt 10, 20, 30, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). Pozițiile în care apar cele mai din dreapta zerouri sunt 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Cel mai din dreapta zero din apare la a 217-a zecimală, cea mai îndepărtată pentru puterile de până la .

	Sloane	astfel încât să nu conțină nici un 0
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, ….

În timp ce nu s-a dovedit că numerele enumerate mai sus sunt singurele fără zerouri pentru o anumită bază, probabilitatea ca orice numere suplimentare să existe este extrem de mică. În această ipoteză, secvența celor mai mari astfel încât să nu conțină zerouri pentru , 3, … este dată atunci de 86, 68, 43, 58, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).