Lineare Regelsysteme verwenden eine negative Rückkopplung, um ein Steuersignal zu erzeugen, das die geregelte PV auf dem gewünschten SP hält. Es gibt mehrere Arten von linearen Regelsystemen mit unterschiedlichen Fähigkeiten.
ProportionalregelungBearbeiten


, wobei ζ {\displaystyle \zeta }

das Dämpfungsverhältnis ist und ω n {\displaystyle \omega _{n}}

ist die ungedämpfte Eigenfrequenz.
Die Proportionalregelung ist eine Art der linearen Rückkopplungsregelung, bei der eine Korrektur auf die Regelgröße angewendet wird, die proportional zur Differenz zwischen dem Sollwert (SP) und dem Messwert (PV) ist. Zwei klassische mechanische Beispiele sind das Schwimmerdosierventil in der Toilettenschüssel und der Fliehkraftregler.
Die Proportionalregelung ist komplexer als eine Ein-Aus-Regelung, aber einfacher als eine Proportional-Integral-Derivativ-Regelung (PID), die z. B. in einem Geschwindigkeitsregler für Autos verwendet wird. Die On-Off-Regelung eignet sich für Systeme, die keine hohe Genauigkeit oder Reaktionsfähigkeit erfordern, ist aber für schnelle und rechtzeitige Korrekturen und Reaktionen nicht geeignet. Die Proportionalsteuerung überwindet dieses Problem, indem sie die Stellgröße (MV), z. B. ein Steuerventil, mit einem Verstärkungsgrad moduliert, der Instabilität vermeidet, aber die Korrektur so schnell wie möglich vornimmt, indem sie die optimale Menge an Proportionalkorrektur anwendet.
Ein Nachteil der Proportionalsteuerung ist, dass sie den verbleibenden SP-PV-Fehler nicht beseitigen kann, da sie einen Fehler benötigt, um einen proportionalen Ausgang zu erzeugen. Um dies zu umgehen, kann ein PI-Regler eingesetzt werden. Der PI-Regler verwendet einen Proportional-Term (P), um den Bruttofehler zu beseitigen, und einen Integral-Term (I), um den verbleibenden Offset-Fehler durch Integration des Fehlers über die Zeit zu beseitigen.
In einigen Systemen gibt es praktische Grenzen für den Bereich des MV. Zum Beispiel kann eine Heizung nur eine bestimmte Wärmemenge erzeugen, und ein Ventil kann nur bis zu einer bestimmten Grenze öffnen. Durch die Einstellung der Verstärkung wird gleichzeitig der Bereich der Fehlerwerte verändert, in dem das MV zwischen diesen Grenzen liegt. Die Breite dieses Bereichs, in Einheiten der Fehlervariablen und damit der PV, wird als Proportionalband (PB) bezeichnet.
OfenbeispielBearbeiten
Bei der Temperaturregelung eines Industrieofens ist es in der Regel besser, die Öffnung des Brennstoffventils proportional zum aktuellen Bedarf des Ofens zu steuern. Auf diese Weise werden Temperaturschocks vermieden und die Wärme wird effektiver zugeführt.
Bei geringen Verstärkungen wird nur eine kleine Korrektur vorgenommen, wenn Fehler entdeckt werden. Das System ist zwar sicher und stabil, reagiert aber unter Umständen träge auf sich ändernde Bedingungen. Fehler bleiben für relativ lange Zeit unkorrigiert und das System ist überdämpft. Wenn die Proportionalverstärkung erhöht wird, reagieren solche Systeme schneller, und Fehler werden schneller behoben. Es gibt einen optimalen Wert für die Verstärkungseinstellung, wenn das Gesamtsystem als kritisch gedämpft bezeichnet wird. Eine Erhöhung der Schleifenverstärkung über diesen Punkt hinaus führt zu Schwingungen in der PV, und ein solches System ist unterdämpft. Die Anpassung der Verstärkung, um ein kritisch gedämpftes Verhalten zu erreichen, wird als Tuning des Regelsystems bezeichnet.
Im Fall der Unterdämpfung heizt der Ofen schnell auf. Sobald der Sollwert erreicht ist, sorgt die gespeicherte Wärme im Teilsystem der Heizung und in den Wänden des Ofens dafür, dass die gemessene Temperatur über das erforderliche Maß hinaus ansteigt. Nachdem die Temperatur über den Sollwert gestiegen ist, fällt sie wieder ab, und schließlich wird erneut Wärme zugeführt. Jede Verzögerung beim Wiederaufheizen des Heizungssystems lässt die Ofentemperatur weiter unter den Sollwert sinken, und der Zyklus wiederholt sich. Die Temperaturschwankungen, die ein unzureichend gedämpftes Ofenregelsystem erzeugt, sind unerwünscht.
In einem kritisch gedämpften System wird die Wärmezufuhr reduziert, wenn sich die Temperatur dem Sollwert nähert, die Aufheizrate des Ofens hat Zeit, sich zu verlangsamen, und das System vermeidet ein Überschwingen. Überschwingen wird auch in einem überdämpften System vermieden, aber ein überdämpftes System reagiert unnötig langsam auf äußere Änderungen am System, z. B. das Öffnen der Ofentür, um den Sollwert zu erreichen.
PID-RegelungBearbeiten

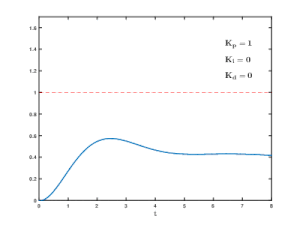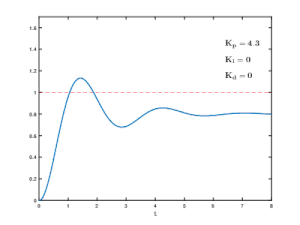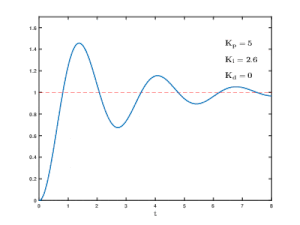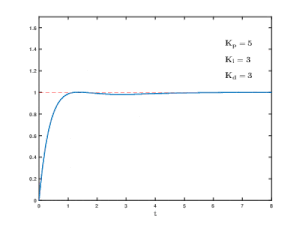
Reine Proportionalregler müssen mit Restfehlern im System arbeiten. Obwohl PI-Regler diesen Fehler eliminieren, können sie dennoch träge sein oder Schwingungen erzeugen. Der PID-Regler behebt diese letzten Unzulänglichkeiten, indem er eine Ableitung (D) einführt, um die Stabilität beizubehalten und gleichzeitig die Reaktionsfähigkeit zu verbessern.
AbleitungBearbeiten
Die Ableitung befasst sich mit der Änderungsrate des Fehlers mit der Zeit: Nähert sich die gemessene Größe schnell dem Sollwert, so wird das Stellglied frühzeitig zurückgefahren, damit es auf den gewünschten Wert auslaufen kann; umgekehrt wird, wenn sich der gemessene Wert schnell vom Sollwert zu entfernen beginnt, eine zusätzliche Anstrengung aufgebracht – proportional zu dieser Geschwindigkeit -, um den Rücklauf zu unterstützen.
Bei Steuerungssystemen, die die Bewegungssteuerung eines schweren Gegenstandes wie eines Gewehrs oder einer Kamera auf einem fahrenden Fahrzeug beinhalten, kann die Ableitung eines gut abgestimmten PID-Reglers es ihm ermöglichen, einen Sollwert besser zu erreichen und zu halten als die meisten erfahrenen menschlichen Bediener. Wenn die Ableitung zu stark angewendet wird, kann sie jedoch zu Schwingungen führen.
IntegralwirkungBearbeiten

Der Integralbegriff vergrößert die Wirkung langfristiger stationärer Fehler, indem er einen immer größeren Aufwand betreibt, bis der Fehler beseitigt ist. Im obigen Beispiel des Ofens, der bei verschiedenen Temperaturen arbeitet, wird, wenn die zugeführte Wärme den Ofen aus irgendeinem Grund nicht auf den Sollwert bringt, der Proportionalbereich durch die Integralwirkung zunehmend relativ zum Sollwert verschoben, bis der PV-Fehler auf Null reduziert und der Sollwert erreicht ist.
Hochfahren in % pro MinuteBearbeiten
Einige Regler bieten die Möglichkeit, das „Hochfahren in % pro Minute“ zu begrenzen. Diese Option kann sehr hilfreich sein, um kleine Heizkessel (3 MBTUH) zu stabilisieren, insbesondere im Sommer bei geringer Last. Ein Heizkessel „kann eine Laständerung von bis zu 5 % pro Minute erfordern (IEA Coal Online – 2, 2007)“.
Andere TechnikenBearbeiten
Es ist möglich, das PV- oder Fehlersignal zu filtern. Dies kann dazu beitragen, Instabilität oder Schwingungen zu verringern, indem die Reaktion des Systems auf unerwünschte Frequenzen reduziert wird. Viele Systeme haben eine Resonanzfrequenz. Durch Herausfiltern dieser Frequenz kann eine stärkere Gesamtrückkopplung angewendet werden, bevor eine Schwingung auftritt, wodurch das System besser reagiert, ohne sich selbst zu erschüttern.
Rückkopplungssysteme können kombiniert werden. Bei der Kaskadenregelung wendet ein Regelkreis Regelalgorithmen auf eine Messgröße in Abhängigkeit von einem Sollwert an, gibt dann aber einen veränderlichen Sollwert an einen anderen Regelkreis weiter, anstatt die Prozessgrößen direkt zu beeinflussen. Hat ein System mehrere verschiedene zu regelnde Messgrößen, so sind für jede von ihnen separate Regelsysteme vorhanden.
In der Regelungstechnik gibt es in vielen Anwendungen Regelsysteme, die komplexer sind als die PID-Regelung. Beispiele für solche Anwendungsgebiete sind Fly-by-Wire-Flugzeugsteuerungen, Chemieanlagen und Ölraffinerien. Modellprädiktive Regelungssysteme werden mit Hilfe spezieller computergestützter Entwurfssoftware und empirischer mathematischer Modelle des zu regelnden Systems entworfen.