Null

Null ist die ganze Zahl mit der Bezeichnung 0, die, wenn sie als Zählzahl verwendet wird, bedeutet, dass keine Objekte vorhanden sind. Sie ist die einzige ganze Zahl (und in der Tat die einzige reale Zahl), die weder negativ noch positiv ist. Eine Zahl, die nicht Null ist, wird als Nicht-Null bezeichnet. Eine Wurzel einer Funktion wird manchmal auch als „eine Null von “ bezeichnet.

Das Schoolhouse Rock-Segment „My Hero, Zero“ preist die Tugenden der Null mit solchen Lobpreisungen wie: „My hero, zero Such a funny little hero But till you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.“

Null wird üblicherweise mit der Faktorisierung angenommen (z.B., im Befehl FactorInteger der Wolfram Language). Andererseits werden die Teiler und die Teilerfunktion im Allgemeinen als undefiniert angesehen, da (d.h. teilt 0) für jede außer Null gilt.

Da die Anzahl der Permutationen von 0-Elementen 1 ist, wird (Nullfaktorial) als 1 definiert (Wells 1986, S. 31). Diese Definition ist nützlich, um viele mathematische Identitäten in einfacher Form auszudrücken.

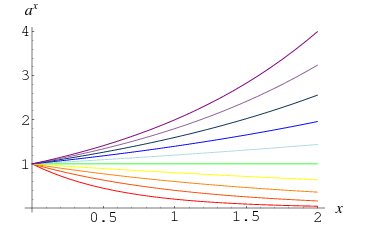
Eine andere Zahl als 0 hoch 0 ist als 1 definiert, was aus dem Grenzwert

Diese Tatsache wird durch die Konvergenz der Kurven bei in der obigen Grafik veranschaulicht, die für , 0.4, …, 2.0. Man kann es auch intuitiver sehen, indem man feststellt, dass die wiederholte Bildung der Quadratwurzel aus einer Zahl immer kleinere Zahlen ergibt, die sich von oben her der Eins annähern, während das Gleiche mit einer Zahl zwischen 0 und 1 immer größere Zahlen ergibt, die sich von unten her der Eins annähern. Für Quadratwurzeln ist die gesamte Potenz , die sich 0 nähert, wenn groß ist, und ergibt, wenn groß ist.

selbst ist nicht definiert. Das Fehlen einer wohldefinierten Bedeutung für diese Größe ergibt sich aus den sich gegenseitig widersprechenden Tatsachen, dass immer 1 ist, so dass gleich 1 sein sollte, aber immer 0 ist (für ), so dass gleich 0 sein sollte. Man könnte argumentieren, dass eine natürliche Definition ist, da

Der Grenzwert existiert jedoch nicht für allgemeine komplexe Werte von . Daher wird die Wahl der Definition für in der Regel als unbestimmt definiert.

Durch die Definition von lassen sich jedoch einige Formeln einfach ausdrücken (Knuth 1992; Knuth 1997, S. 57), ein Beispiel dafür ist die schöne analytische Formel für das Integral der verallgemeinerten sinc-Funktion

gegeben von Kogan (vgl. Espinosa und Moll 2000), wobei , und die Bodenfunktion ist.

Richardsons Theorem ist ein grundlegendes Ergebnis der Entscheidbarkeitstheorie, das besagt, dass die Bestimmung, ob auch einfache Ausdrücke identisch gleich Null sind, prinzipiell unentscheidbar ist, geschweige denn in der Praxis.

Die folgende Tabelle gibt die ersten Zahlen an, bei denen die Dezimalentwicklung von für kleine keine Nullen enthält (ein Problem, das der Gelfand-Frage ähnelt). Die größte bekannte , für die keine Nullen enthält, ist 86 (Madachy 1979), mit keiner anderen (M. Cook, pers. Mitt., 26. September 1997 und 16. März 1998), wodurch die von Beeler und Gosper (1972) ermittelte Grenze von verbessert wird. Die Werte , bei denen die Positionen der äußersten rechten Null in zunehmen, sind 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). Die Stellen, an denen die Nullen ganz rechts vorkommen, sind 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). Die äußerste rechte Null von steht an der 217. Dezimalstelle, der am weitesten entfernten für Potenzen bis .

	Sloane	so dass keine 0en enthält
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, ….

Es ist zwar nicht bewiesen, dass die oben aufgeführten Zahlen die einzigen ohne Nullen für eine gegebene Basis sind, aber die Wahrscheinlichkeit, dass es noch weitere Zahlen gibt, ist verschwindend gering. Unter dieser Annahme ist die Folge der größten , so dass keine Nullen für , 3, … enthält, gegeben durch 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).