Nul

Nul is het gehele getal 0 dat, wanneer het als telgetal wordt gebruikt, betekent dat er geen voorwerpen aanwezig zijn. Het is het enige gehele getal (en in feite het enige reële getal) dat noch negatief noch positief is. Van een getal dat niet nul is, wordt gezegd dat het niet nul is. Een wortel van een functie wordt soms ook “een nul van ” genoemd.”

Het Schoolhouse Rock-segment “My Hero, Zero” prijst de deugden van nul met lofuitingen als: “My hero, zero Such a funny little hero But till you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.”

Zero wordt gewoonlijk genomen om de factorisatie te hebben (bijv, in het commando FactorInteger van de Wolfram-taal). Anderzijds worden de delers en de delerfunctie over het algemeen als ongedefinieerd beschouwd, omdat volgens conventie (d.w.z. deelt 0) voor elke behalve nul.

Omdat het aantal permutaties van 0-elementen 1 is, is (nulfactor) gedefinieerd als 1 (Wells 1986, p. 31). Deze definitie is nuttig om veel wiskundige identiteiten in eenvoudige vorm uit te drukken.

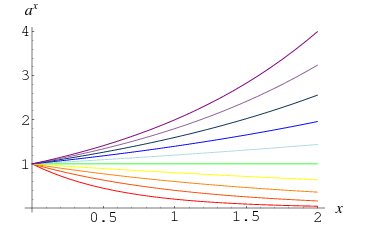
Een ander getal dan 0 tot de macht 0 is gedefinieerd als 1, hetgeen volgt uit de limiet

Dit feit wordt geïllustreerd door de convergentie van krommen bij in de bovenstaande grafiek, die laat zien voor , 0.4, …, 2.0. Het kan ook intuïtiever worden gezien door op te merken dat het herhaald nemen van de vierkantswortel van een getal steeds kleinere getallen oplevert die van bovenaf één naderen, terwijl hetzelfde doen met een getal tussen 0 en 1 steeds grotere getallen oplevert die van onderaf één naderen. Voor vierkantswortels is de totale macht , die 0 nadert als groot is, en oplevert in de limiet dat groot is.

zelf is ongedefinieerd. Het ontbreken van een goed gedefinieerde betekenis voor deze grootheid volgt uit de onderling tegenstrijdige feiten dat altijd 1 is, dus gelijk moet zijn aan 1, maar is altijd 0 (voor ), dus moet gelijk zijn aan 0. Men zou kunnen stellen dat een natuurlijke definitie is, omdat

De limiet bestaat echter niet voor algemene complexe waarden van . Daarom wordt de keuze van de definitie voor gewoonlijk als onbepaald gedefinieerd.

Het definiëren van maakt het echter mogelijk sommige formules eenvoudig uit te drukken (Knuth 1992; Knuth 1997, p. 57), waarvan een voorbeeld de mooie analytische formule is voor de integraal van de veralgemeende sinc-functie

gegeven door Kogan (cf. Espinosa en Moll 2000), waarbij , , en de bodemfunctie is.

Richardson’s stelling is een fundamenteel resultaat in de decidabiliteitstheorie dat vaststelt dat de bepaling of zelfs eenvoudige uitdrukkingen identiek gelijk zijn aan nul in principe onbeslisbaar is, laat staan in de praktijk.

De volgende tabel geeft de eerste getallen zodanig dat de decimale uitbreiding van geen nullen bevat voor kleine (een probleem dat lijkt op de vraag van Gelfand.) De grootst bekende waarvoor geen nullen bevatten is 86 (Madachy 1979), met geen andere (M. Cook, pers. comm., 26 sep. 1997 en 16 mrt. 1998), waarmee de limiet van Beeler en Gosper (1972) wordt verbeterd. De waarden zodanig dat de posities van de meest rechtse nul in toenemen zijn 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). De posities waarin de meest rechtse nullen voorkomen zijn 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). De meest rechtse nul van komt voor op de 217e decimaal, het verst over voor machten tot .

	Sloane	zodanig dat geen 0’s bevat
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …

Hoewel niet bewezen is dat de hierboven opgesomde getallen de enige zijn zonder nullen voor een gegeven grondtal, is de kans dat er nog meer nullen bestaan wel heel erg klein. Onder deze aanname is de rij grootste zodanig dat geen nullen bevat voor , 3, … gegeven door 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).