ゼロは0と表記される整数で、数を数えるときに、物が存在しないことを意味する。 これは、負でも正でもない唯一の整数（事実上、唯一の実数）である。 ゼロでない数を非ゼロという。 関数 
のルートは「
のゼロ」とも呼ばれることがある。
The Schoolhouse Rock segment “My Hero, Zero” は、「私のヒーロー、ゼロ、こんなにおかしな小さなヒーロー、でもあなたが現れるまで私たちは指やつま先で数えた。”
ゼロは一般に因数分解
を持つとされている（例． を持つものとして扱われる（例：Wolfram LanguageのFactorIntegerコマンド）。 一方、約数や約数関数
は、慣例により0以外のすべての
に対して
（つまり
は0を割る）ので、一般に不定とされる。
0要素の順列の数は1なので、
（0の階乗）は1と定義される（Wells 1986, p.31）。 この定義は、多くの数学的恒等式を簡単な形で表現するのに便利である。
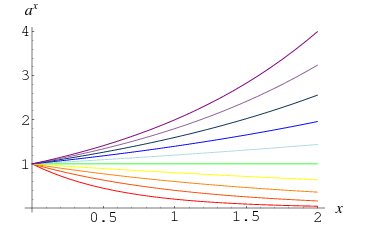
0以外の数の0乗は1と定義され、これは極限
 |
(1)
|
この事実は上記のプロットの 
でカーブが集中し、 
, 0.0 に対して 
となっていることから理解されよう。4, …, 2.0. また、
という数の平方根を繰り返しとると、上から1へ近づくほど小さくなり、0と1の間の数で同じことをすると、下から1へ近づくほど大きくなることに注目すれば、より直感的にわかるでしょう。 
の平方根の場合、取られる総電力は
で、
が大きくなると0に近づき、
が大きい極限で
となる。
自体は未定義である。 この量に明確な意味がないのは、
は常に1なので
は1になるはずだが、
は（
に対して）常に0なので
は0になるという互いに矛盾する事実があるためである。 5471>
 |
(2)
|
しかし、
の一般の複素値では極限が存在しないので自然定義と言えるでしょう。 したがって、
の定義の選択は通常不定と定義される。
しかし、
を定義すると、いくつかの式が簡単に表現できるようになる（Knuth 1992; Knuth 1997, p. 57)、その一例がKoganによって与えられた一般化sinc関数
 |
(3)
|
の積分の美しい解析式であり（参照：エスピノーサとモール2000）、
, 
, 
は階関数と呼ばれるもの。
リチャードソンの定理は、単純な式が同一に0に等しいかどうかの判定が、実際にはともかく原理的には決定不可能であることを立証した、決定可能性理論の基本結果である。
次の表は、小さな
に対して
の10進展開がゼロを含まないような数
を最初にいくつか示しています（Gelfandの問題に似た問題）。
がゼロを含まない最大の
は86 (Madachy 1979) で、それ以外の
はありません (M.Cook, pers. comm, M. Cook, pers. 26, 1997 and Mar. 16, 1998) であり、Beeler and Gosper (1972) が得た
の限界は改善されている。 8105＞の右端のゼロの位置が増加するような値＜2883＞は、10、20、30、40、46、68、93、95、129、176、229、700、1757、1958、7931、57356、269518、……である。 (OEIS A031140)。 右端のゼロが発生する位置は、2、5、8、11、12、13、14、23、36、38、54、57、59、93、115、119、120、121、136、138、164、……である。 (OEIS A031141)。 
の右端の0は小数点以下217桁目にあり、
までの累乗では最も端にある。
 |
Sloane | このように は0を含まない |
| 2 | A007377 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, … |
| 3 | A030700 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, … |
| 4 | A030701 | 1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, … |
| 5 | A008839 | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, … |
| 6 | A030702 | 1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, … |
| 7 | a030703 | 1, 2, 3, 6, 7, 10, 11, 19, 35 |
| 8 | a030704 | 1、2、3、5、6、8、9、11、12、13、17、24、。 27 |
| 9 | A030705 | 1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34 |
| 11 | A030706 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, …. |
与えられた基数に対して、上に挙げた数だけがゼロのない数であることは証明されていないが、それ以外の数が存在する確率はきわめて小さい。 この仮定の下で、
が
, 3, …に対して0を含まないような最大の
の並びは、86, 68, 43, 58, 44, 35, 27, 34, 0, 41, …で与えられる。 (OEIS A020665).
である。