I vari tipi di controllori sono usati per migliorare le prestazioni dei sistemi di controllo. In questo capitolo, discuteremo i controllori di base come il proporzionale, il derivato e l’integrale.
Controllore proporzionale
Il controllore proporzionale produce un’uscita, che è proporzionale al segnale di errore.
$$u(t) \proto e(t) $$
$$$Freccia destra u(t)=K_P e(t)$$
Applica la trasformata di Laplace su entrambi i lati –
$$U(s)=K_P E(s)$$
$$$frac{U(s)}{E(s)}=K_P$$
Quindi, la funzione di trasferimento del regolatore proporzionale è $K_P$.
Dove,
U(s) è la trasformata di Laplace del segnale di attuazione u(t)
E(s) è la trasformata di Laplace del segnale di errore e(t)
KP è la costante di proporzionalità
Lo schema a blocchi del sistema di controllo ad anello chiuso a retroazione negativa unitaria con il regolatore proporzionale è mostrato nella figura seguente.
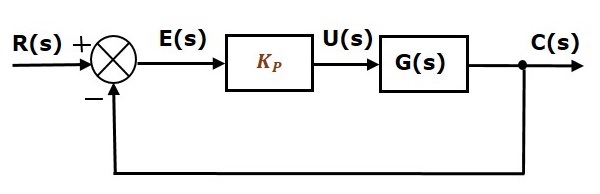
Il controllore proporzionale è usato per cambiare la risposta transitoria secondo il requisito.
Controllore derivativo
Il controllore derivativo produce un’uscita, che è derivata del segnale di errore.
$$u(t)=K_D \frac{\testo{d}e(t)}{\testo{d}t}$
Applica la trasformazione di Laplace su entrambi i lati.
$$U(s)=K_D sE(s)$$
$$$frac{U(s)}{E(s)}=K_D s$
Quindi, la funzione di trasferimento del controllore derivativo è $K_D s$.
dove, $K_D$ è la costante di derivazione.
Lo schema a blocchi del sistema di controllo ad anello chiuso a retroazione negativa unitaria con il controllore derivativo è mostrato nella figura seguente.
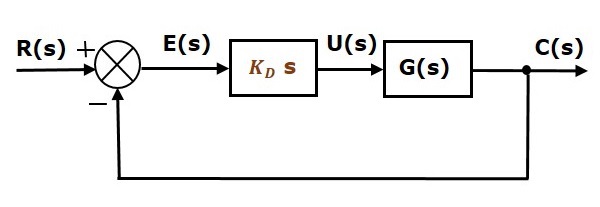
Il controllore derivativo è usato per rendere il sistema di controllo instabile in uno stabile.
Controllore integrale
Il controllore integrale produce un’uscita, che è integrale del segnale di errore.
$$u(t)=K_I \int e(t) dt$
Applica la trasformata di Laplace su entrambi i lati –
$$U(s)=\frac{K_I E(s)}{s}$
$$==frac{K_I}{s}$
Quindi, la funzione di trasferimento del controllore integrale è $\frac{K_I}{s}$.
Dove, $K_I$ è la costante integrale.
Lo schema a blocchi del sistema di controllo ad anello chiuso a retroazione negativa unitaria insieme al controllore integrale è mostrato nella figura seguente.
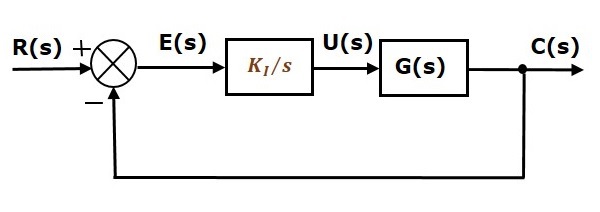
Il controllore integrale è usato per diminuire l’errore di stato stazionario.
Discutiamo ora della combinazione dei controllori di base.
Controllo proporzionale-derivativo (PD)
Il controllore proporzionale-derivativo produce un’uscita, che è la combinazione delle uscite dei controllori proporzionali e derivati.
$$u(t)=K_P e(t)+K_D \frac{{testo{d}e(t)}{testo{d}t}$
Applica la trasformata di Laplace su entrambi i lati –
$$U(s)=(K_P+K_D s)E(s)$$
$$$frac{U(s)}{E(s)}=K_P+K_D s$
Quindi, la funzione di trasferimento del regolatore proporzionale derivato è $K_P + K_D s$.
Lo schema a blocchi del sistema di controllo ad anello chiuso a retroazione negativa unitaria con il controllore proporzionale derivativo è mostrato nella figura seguente.
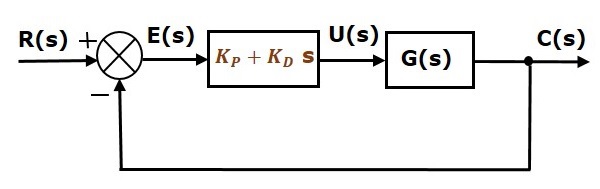
Il controllore proporzionale derivato è usato per migliorare la stabilità del sistema di controllo senza influenzare l’errore di stato stazionario.
Controllore proporzionale integrale (PI)
Il controllore proporzionale integrale produce un’uscita, che è la combinazione delle uscite dei controllori proporzionale e integrale.
$$u(t)=K_P e(t)+K_I \int e(t) dt$
Applica la trasformata di Laplace su entrambi i lati –
$$U(s)=\sinistra(K_P+frac{K_I}{s} \destra )E(s)$$
$$$frac{U(s)}{E(s)}=K_P+frac{K_I}{s}$
Quindi, la funzione di trasferimento del regolatore integrale proporzionale è $K_P + \frac{K_I} {s}$.
Lo schema a blocchi del sistema di controllo ad anello chiuso a retroazione negativa unitaria con il controllore integrale proporzionale è mostrato nella figura seguente.
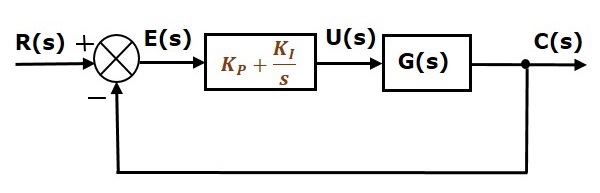
Il controllore integrale proporzionale è usato per diminuire l’errore di stato stazionario senza influenzare la stabilità del sistema di controllo.
Controllore proporzionale integrale derivativo (PID)
Il controllore proporzionale integrale derivativo produce un’uscita, che è la combinazione delle uscite dei controllori proporzionale, integrale e derivativo.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac {testo{d}e(t)}{testo{d}t}$
Applica la trasformata di Laplace su entrambi i lati –
$$U(s)==Sinistra(K_P+frac{K_I}{s}+K_D s \destra )E(s)$$
$$$frac{U(s)}{E(s)}=K_P+frac{K_I}{s}+K_D s$$
Quindi, la funzione di trasferimento del regolatore proporzionale integrale derivativo è $K_P + \frac{K_I} {s} + K_D s$.
Lo schema a blocchi del sistema di controllo ad anello chiuso a retroazione negativa unitaria con il controllore proporzionale integrale derivativo è mostrato nella figura seguente.
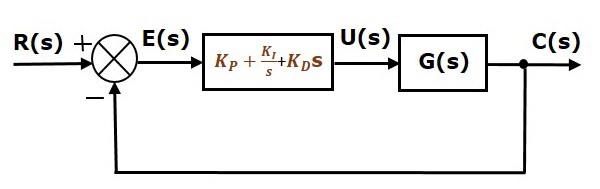
Il controllore proporzionale integrale derivativo è usato per migliorare la stabilità del sistema di controllo e per diminuire l’errore di stato stazionario.