Una domanda importante è: come sono distribuiti i numeri primi tra i numeri interi? La risposta è, in poche parole, piuttosto casuale, date certe statistiche di base…
 Bill Casselman
Bill Casselman
Università della British Columbia, Vancouver, Canada
Email Bill Casselman
| |
|
Introduzione
Molti anni fa è stato congetturato che esiste un numero infinito di coppie di numeri primi $p$, $q$ con $q = p+2$. Ci sono stati alcuni recenti (e famosi) progressi su questo problema. Dirò poco sui progressi recenti, ma discuterò invece ciò che ci aspettiamo – piuttosto che ciò che sappiamo – su tali coppie. Nulla di ciò che dirò è nuovo, e in una certa misura ho semplicemente elaborato ciò che Andrew Granville dice nella sua recente nota espositiva sui recenti progressi.
Quanti primi ci aspettiamo?
Un numero primo è un intero positivo che non ha divisori tranne se stesso e $1$. La definizione è semplice, ma non appena si inizia ad esplorare il significato dei numeri primi ci si rende conto che essi mostrano un comportamento molto più sottile. Una domanda importante è: come sono distribuiti i numeri primi tra i numeri interi? La risposta è, in poche parole, piuttosto casualmente, date certe statistiche di base. Cosa intendo con questo?
Ebbene, ecco una matrice quadrata che rappresenta tutti i numeri primi fino a 400$:

Ci sono alcuni schemi in questa matrice, alcuni dei quali li commenterò più avanti. La maggior parte di quelli che percepite sono causati da qualche artefatto del display. Per esempio, una colonna su due è essenzialmente vuota, e questo perché l’unico primo pari è $2$. Inoltre, ogni quinta colonna è essenzialmente vuota. Più interessanti sono le coppie di primi gemelli (alcune delle quali non sono così visibili perché si dividono in due righe, come $59$, $61$), e anche alcuni modelli relativi alle ultime cifre visualizzate. Questi sono quelli che potremmo chiamare schemi locali. Non ci sono schemi globali evidenti.
Ci sono stati molti sforzi per trovare modi estremamente efficienti per produrre numeri primi, ma al giorno d’oggi anche un programma molto semplice richiede solo una piccola quantità di tempo per fare grandi liste di numeri primi. Uno dei programmi più fruttuosi farà una grande lista di numeri primi e poi la userà per calcolare la funzione $\pi(n)$, il numero di numeri primi $\le n$.
Una cosa per cui questo può essere usato è per avere un’idea approssimativa della frequenza dei primi. Ci sono $135$ primi nell’intervallo $$:
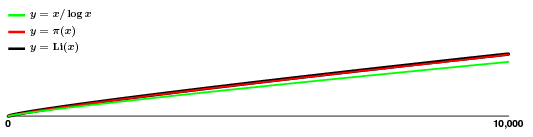
L’approssimazione sembra ottima! Quindi, anche se $\pi(x)$ rimbalza un po’, apparentemente senza molto schema, abbiamo una stima abbastanza buona per esso, il che significa che abbiamo una buona idea di come crescono i primi, almeno in media.
Si dovrebbe tenere a mente, tuttavia, che l’apparente morbidezza è ingannevole. Da vicino, ecco come appaiono le due curve superiori:

Commenti?
Ragionamento euristico sui numeri primi gemelli
I numeri primi gemelli sono una coppia $p$, $p+2$ che sono entrambi primi. Per esempio, da uno dei grafici sopra vediamo i primati gemelli $$ , , , , , , $$
e altri. È stato ipotizzato che ce ne siano un numero infinito, ma anche se ci sono molte prove empiriche per questo, non è stato ancora dimostrato.
Forse la prova più forte è una formula che approssima il numero $\pi_{2}(x)$ di numeri primi gemelli $\le x$ notevolmente bene. Non sono del tutto sicuro dell’origine di questa formula, ma è apparsa per la prima volta in un articolo di G. H. Hardy e J. E. Littlewood (essi stessi una coppia di primi gemelli) datato 1923. L’articolo contiene diverse formule simili, tutte basate sullo stesso metodo, che avevano usato per attaccare molti problemi precedenti. Questo era il loro metodo del cerchio. La loro derivazione della formula per $\pi_{2}(x)$ non è affatto rigorosa, ma è molto convincente. C’è un succinto resoconto di questo in un’appendice all’articolo di Andrew Granville.
Ma subito dopo la seconda guerra mondiale Lord Cherwell (Frederick Lindemann) suggerì una derivazione probabilistica più elementare (e ancora non rigorosa). Questo portò a una collaborazione con E. M. Wright e infine a una pubblicazione congiunta postuma. Questo è spiegato nella sezione 22.20 del noto testo di Hardy e Wright. Una versione leggermente più elementare di questo può essere trovata anche in un’appendice dell’articolo di Granville (Sezione 2.5). Io lo seguo.
Il punto di partenza del ragionamento plausibile è la nostra stima per $\pi(x)$, il numero di primi minori o uguali a $x$. L’idea di base della derivazione è che i numeri primi sono, in buona misura, distribuiti in modo casuale. Sappiamo che nelle vicinanze di $x$ la densità dei numeri primi è circa $1/log x$. Se i numeri primi fossero distribuiti casualmente, allora la probabilità che due numeri qualsiasi vicino a $x$ siano primi sarebbe solo il prodotto delle probabilità locali, che è $1/\log^{2} x$. Questo è certamente un ragionamento specioso, poiché se $n > 2$ la probabilità che sia $n$ che $n+1$ siano primi è $0$, mentre il fatto che $p$ sia un primo sembrerebbe aumentare le probabilità che $p+2$ lo sia. Ci sono considerazioni simili da tenere in considerazione per la possibile divisibilità con altri piccoli primi, anche nelle vicinanze di $x$.
C’è un fatto semplice in questa storia. Se $q$ è un qualsiasi primo, allora la probabilità di scegliere un intero a caso che non sia divisibile per $q$ è $1-1/q$. La probabilità di sceglierne due non divisibili per $q$ è quindi il prodotto $(1 – 1/q)^{2}$. Supponiamo che $p$ e $p+2$ siano entrambi primi, allora né $p$ né $p+2$ sono divisibili per $q$. Se $q = 2$, questo accade 1/2$ delle volte. Se $q è 2$, la probabilità che $p non sia uguale a 0$ e $p non sia uguale a -2$ modulo $q$ è $(1 – 2/q)$. A causa del Teorema del resto cinese, la divisibilità per due primi è un evento indipendente. Quindi se $x$ è grande e $Q$ è relativamente piccolo la probabilità che una qualsiasi coppia di numeri $m$ e $n$ vicino a $x$ non sia un multiplo di un primo fino a $Q$ è $$ { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \$$
Lasciamo che $Gamma_{Q}$ sia il rapporto di questo con $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\su 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \su (1 – 2/q) } $$ Abbiamo $$ { 1 – 2/q \su (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \su (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \Un criterio standard asserisce che questo prodotto converge se la somma 1/(q-1)^{2}$ converge. Ma esso converge poiché il test integrale ci dice che la somma 1/n^{2}$ converge. Quindi questo prodotto converge effettivamente ad un numero $Pi_{\infty}$ come $Q \rightarrow \infty$. Sia $C_{2}$ il suo inverso. La sezione 2.5 dell’articolo di Granville dice che a questo punto dovrebbe essere intuitivamente ragionevole che il numero $\pi_{2}(x)$ di primati gemelli $\le x$ è approssimato da $$ \Pi_{2}(x) = C_{2} \int_{2}^{infty} { dx \ su \log^{2} x } \$$
Il testo di Hardy e Wright presenta un’analisi più attenta che rende il salto intuitivo un po’ più chiaro.
Il valore della costante qui è stato calcolato molto tempo fa da J. W. Wrench per essere circa $1.32032363169373914785562422002911155686525 \ldots $. Ecco un confronto tra alcuni valori di $\pi_{2}(x)$ e la formula nell’intervallo $$: $$ \matrice{ n & 10.000 & 20.000 & 30.000 & 40.000 & 50.000 \cr \pi_{2}(n) & 205\fantom{.0} & 342 \fantasma{.0} & 467 \fantasma{.0} & 591 \fantasma{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } $$ $$ \matrice{ n & 60.000 & 70.000 & 80.000 & 90.000 & 100.000 \cr \pi_{2}(n) & 811 \fantom{.0} & 905 \fantasma{.0} & 1007 \fantasma{.0} & 1116 \phantom{.0} & 1224 \phantom{.0} \cr \Pi_{2}(x) & 833,3 & 940,9 & 1045,7 & 1148,2 & 1248,7 \cr } $$
Commenti?
La congettura di Dickson
I primati gemelli sono un caso speciale di qualcosa di molto più generale. Ci si può chiedere: ci sono un numero infinito di coppie $p$, $p+4$ o $p$, $p+6$ che sono primi? O $p$, $p+10$? Il caso di $p$ e $p+10$ è certamente suggerito da una delle immagini qui sopra, in cui tali coppie sono facilmente visibili. Che ne dite di triple di qualche tipo? Supponiamo che $a_{1}$, $a_{2}$, $a_ldots$ , $a_{k}$ costituiscano un array di numeri interi. Possiamo aspettarci che ci sia un numero infinito di insiemi $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ che sono tutti primi?
Si deve stare un po’ attenti. Non ci sono coppie prime della forma $p$, $p+1$ (dopo $p = 2$), perché uno di questi due numeri deve essere divisibile per $2$. Allo stesso modo, dopo $p = 3$ non ci sono triple prime $p$, $p+2$, $p+4$ perché una di queste deve essere divisibile per $3$.
Questo ultimo esempio dovrebbe essere illuminante. Il numero $p+4$ è divisibile per $3$ se e solo se $p+1$ è divisibile per $3$. Quindi $3$ divide uno dei numeri $p$, $p+2$, $p+4$ se e solo se divide $p$, $p+1$, $p+2$. Ma questo accade di sicuro, poiché l’ultima tripla copre chiaramente tutti i numeri modulo $3$.
In generale, si dice che $p$ è un’ostruzione per l’array $(a_{i})$ se $p$ divide sempre almeno uno di ogni sequenza $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Questo accade se e solo se i numeri $a_{i} \; {\rm mod} \, p$ riempiono tutta $Z/p$.
Questo non può mai accadere se $p > k$, quindi per controllare se qualche $p$ ostacola $(a_{i})$ dobbiamo solo controllare se i $a_{i}$ coprono $Z/p$ per tutti i $p \le k$. Chiamiamo la matrice $(a_{i})$ ammissibile se non ha ostruzioni prime.
Per esempio, $(1,3,7,9)$ è una matrice ammissibile, poiché, come si può verificare facilmente, né $2$ né $3$ sono un’ostruzione. Diverse sequenze di primi che rientrano in questo schema possono essere viste in uno dei diagrammi qui sopra. Altri esempi sono (a) qualsiasi $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Esistono insiemi ammissibili arbitrariamente grandi. Infatti:
Teorema. Se da $a_{1}$ a $a_{k}$ è un qualsiasi insieme di primi distinti $> k$, essi costituiscono un insieme ammissibile.
Perché? Se $p$ è un qualsiasi primo dove $p> k$, allora abbiamo già visto che non può essere un’ostruzione. Ma se $p \le k$, allora non può dividere nessuno degli $a_{i}$, nessuno dei quali può essere congruente a $0$ modulo $p$. Quindi gli $a_{i}$ non riempiono $Z/p$.
Un caso speciale di una congettura fatta originariamente da L. E. Dickson è che se non ci sono ostacoli primi a $(a_{i})$ allora esiste un numero infinito di sequenze prime della forma $(n +a_{i})$.
Cosa è successo di recente
Non è questo il luogo per raccontare tutta la storia, che è stata trattata a fondo in altri luoghi. Raccomando in particolare l’articolo Quanta di Erica Klarreich per un resoconto popolare, e il saggio di Granville per uno più tecnico. Voglio solo dichiarare un po’ più precisamente che nel resoconto di Klarreich qual è il più famoso dei nuovi risultati.
È dovuto a Yitang Zhang. L’affermazione più semplice di ciò che ha dimostrato è che esiste un numero infinito di intervalli $[n, n+70.000.000)$ contenenti almeno due primi. Questo è più debole della congettura dei primati gemelli, ma concettualmente molto vicino ad essa. In lavori successivi (di molti matematici) la dimensione del divario è stata fortemente ridotta, ma presumibilmente non c’è modo di ridurla a $2$ con i metodi attuali.
Come spiegato da Granville, il primo e probabilmente principale risultato di Zhang è che esiste $k$ con la proprietà che se $a_{1}$, $\ldots$ , $a_{k}$ è un insieme ammissibile di $k$ elementi, allora esiste un numero infinito di $n$ tale che ${ n +a_{i} \i}$ contenga almeno due primi. (Nell’articolo di Klarreich su Quanta, la matrice è chiamata “pettine”. Tenete a mente che secondo la congettura di Dickson, ci aspetteremmo di poter dire che tutti gli $k$ sono primi). Infatti, Zhang ha dimostrato che questa affermazione è vera per un particolare $k =3.500.000$ che abbraccia un intervallo di $70.000.000$. L’ormai famosa conseguenza è che per alcuni $m \lt 70.000.000$ esiste un numero infinito di coppie di primi $p$, $p+m$.
Leggendo oltre
- Lord Cherwell e E. M. Wright, “The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Chi conosce qualcosa della vita di Lord Cherwell, altrimenti noto come Frederick Lindemann, sarà molto sorpreso di apprendere del suo contributo alla teoria dei numeri. La biografia di Wikipedia non suggerisce adeguatamente tutte le ragioni della sua cattiva reputazione come principale consigliere scientifico di Churchill durante la seconda guerra mondiale.
- L. E. Dickson, “A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Vedi anche la voce di Wikipedia sulla congettura di Dickson.
- Andrew Granville, “Numeri primi in intervalli di lunghezza limitata”. Disponibile dalla sua home page.
- G. H. Hardy, Ramanujan, Cambridge University Press.
La sezione 2.5 contiene una derivazione ideale di una possibile formula per $\pi(x)$.
- G. H. Hardy e J. E. Littlewood, “Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy and E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, “Together and alone, closing the prime gap”, Quanta 19 novembre 2013.
- B. Riemann, “Sul numero dei numeri primi inferiori a una data quantità”. Una traduzione inglese di questo classico da parte di David Wilkins è disponibile da un link in Wikipedia.
Tra le altre cose, questo abbozza una derivazione della formula approssimativa per $\pi(x)$.
- J. W. Wrench, “Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
Un primo calcolo di $C_{2}$.
- Liste di numeri primi fino a $1.000.000.000.000$
- Una lista dei primi 20.000 numeri primi gemelli.
 Bill Casselman
Bill Casselman
Università della British Columbia, Vancouver, Canada
Email Bill Casselman