Modellazione matematica

Alcune funzioni sono a pezzi. In questa sezione, impareremo come definire e rappresentare graficamente funzioni che sono essenzialmente collezioni di pezzi discreti. Esempi di qualcosa definito in questo modo includono la progettazione del profilo di un’auto, il calcolo del vostro piano di telefonia mobile, e il calcolo delle aliquote delle imposte sul reddito. Per esempio, la vostra aliquota fiscale dipende dal vostro reddito ed è la stessa per una gamma di redditi, come è mostrato nella tabella qui sotto:

Una funzione piecewise è una funzione in cui più di una formula è usata per definire l’uscita su diversi pezzi del dominio.

Utilizziamo le funzioni piecewise per descrivere situazioni in cui una regola o una relazione cambia quando il valore di input attraversa certi “confini”. Per esempio, incontriamo spesso situazioni negli affari in cui il costo per pezzo di un certo articolo viene scontato una volta che il numero ordinato supera un certo valore. Gli scaglioni fiscali sono un altro esempio nel mondo reale di funzioni piecewise. Per esempio, consideriamo un semplice sistema fiscale in cui i redditi fino a 10.000 dollari sono tassati al 10%, e ogni altro reddito è tassato al 20%. La tassa su un reddito totale, S, sarebbe 0,1S se S è uguale a $10.000 e 1000 + 0,2 (S – $10.000), se S> $10.000.

Valutare una funzione definita piecewise

Nel primo esempio, mostreremo come valutare una funzione definita piecewise. Notate come sia importante prestare attenzione al dominio per determinare quale espressione usare per valutare l’input.

Nel seguente video mostriamo come valutare diversi valori data una funzione definita in modo parziale.

Nel prossimo esempio mostriamo come valutare una funzione che modella il costo del trasferimento dati per una compagnia telefonica.

Analisi della soluzione

La funzione è rappresentata nel grafico sottostante. Possiamo vedere dove la funzione cambia da una costante a una linea con una pendenza positiva a g=2. Tracciamo i grafici per le diverse formule su un insieme comune di assi, assicurandoci che ogni formula sia applicata sul suo giusto dominio.

C(g) = C\sinistra(g\destra)=== inizio{casi}{25}{ testo{ se } 0 }<{ g }<{ 2 }{ 10g+5{ testo{ se }{ g}{ 2 } fine{casi}

Scrivere una funzione definita in modo frammentario

Nell’ultimo esempio mostreremo come scrivere una funzione definita in modo frammentario che modella il prezzo di una visita guidata al museo.

Analisi della soluzione

La funzione è rappresentata nella Figura 21. Il grafico è una linea diagonale da n=0 a n=10 e una costante dopo. In questo esempio, le due formule concordano nel punto d’incontro in cui n=10, ma non tutte le funzioni a compartimenti stagni hanno questa proprietà.

Nel seguente video mostriamo un esempio di scrittura di una funzione definita a compartimenti stagni dato uno scenario.

Grafico di funzioni dipendenti

In questa sezione, tracceremo funzioni dipendenti. La funzione tracciata qui sotto rappresenta il costo di trasferimento dei dati per una data compagnia di telefonia mobile. Possiamo vedere dove la funzione cambia da una costante a una linea con una pendenza positiva a g=2. Quando tracciamo le funzioni piecewise, è importante assicurarsi che ogni formula sia applicata al suo corretto dominio.C\left(g\right)=\begin{casi}{25} \testo se 0 }<{ g }<{ 2 }10g+5 {testo se g}ge{ 2 }fine{casi}

In questo caso, l’output è 25 per qualsiasi input tra 0 e 2. Per valori uguali o superiori a 2, l’output è definito come 10g+5.

Esempio

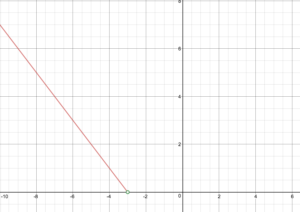
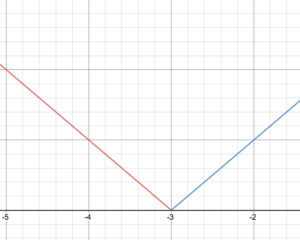
Segnala un grafico della funzione.

Data la definizione piecewise f(x)=\inizio{caso}-x – 3\testo{ se }x < -3\ x + 3\testo{ se } x \ge -3\fine{casi}
Disegna il grafico di f.
Dichiara il dominio e l’intervallo della funzione.

Mostra la risposta

Prima di tutto, traccia il grafico della linea f(x) = -x-3, cancellando la parte in cui x è maggiore di -3. Posiziona un cerchio aperto in corrispondenza di (-3,0).

Posiziona ora la retta f(x) = x+3 sul grafico, partendo dal punto (-3,0). Si noti che per questa porzione del grafico, il punto (-3,0) è incluso, quindi si può rimuovere il cerchio aperto.

I due grafici si incontrano nel punto (-3,0)

Il dominio di questa funzione è di tutti i numeri reali perché (-3,0)non è incluso come punto finale di f(x) = -x-3, ma è incluso come punto finale per f(x) = x+3.

L’intervallo di questa funzione inizia da f(x)=0 e include 0, e va all’infinito, quindi lo scriveremmo come x\ge0

Nel prossimo esempio, disegneremo una funzione definita a tratti che modella il costo della spedizione per un rivenditore di fumetti online.

Esempio

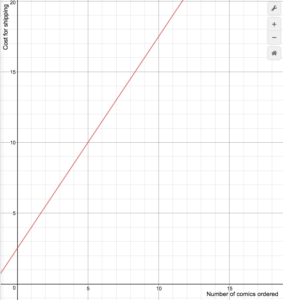
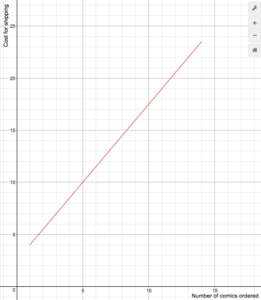
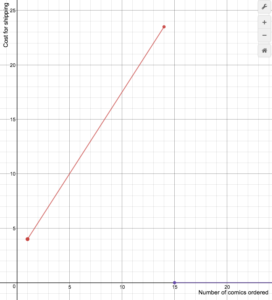
Un rivenditore di fumetti online addebita le spese di spedizione secondo la seguente formula

S(n)==begin{casi}1.5n+2.5\testo se 1\le{n}le14\0\testo se 1\ge15\fine{casi}

Disegna un grafico della funzione di costo.

Mostra risposta

Prima di tutto, traccia la linea S(n)=1.5n+2.5. Possiamo usare le trasformazioni: questo è un tratto verticale dell’identità di un fattore 1,5, e uno spostamento verticale di 2,5.

S(n)=1,5n+2.5

Ora possiamo eliminare le porzioni del grafico che non sono nel dominio basato su 1\le{n}\le14

S(n) = 1,5n+2,5 per 1<=n<=14

Infine, aggiungere la funzione costante S(n)=0 per ingressi maggiori o uguali a 15. Mettete dei punti chiusi alle estremità del grafico per indicare l’inclusione dei punti finali.

Nel seguente video mostriamo come tracciare il grafico di una funzione definita piecewise che è lineare su entrambi i domini.

Sommario

• Una funzione piecewise è una funzione in cui più di una formula è usata per definire l’output su diverse parti del dominio.
• Valutare una funzione piecewise significa che dovete prestare molta attenzione all’espressione corretta usata per l’input dato

Per graficare funzioni piecewise, prima identificate dove è diviso il dominio. Graficare le funzioni sul dominio usando strumenti come i punti di tracciatura o le trasformazioni. Fai attenzione ad usare cerchi aperti o chiusi sui punti finali di ogni dominio in base al fatto che il punto finale sia incluso.