Mezzo Adder e Circuito Full Adder
I circuiti Half Adder e Full Adder sono spiegati con le loro tabelle della verità in questo articolo. Viene anche mostrato il progetto di Full Adder utilizzando il circuito Half Adder. Viene anche mostrato il circuito Full Adder a un bit e l’addizione a più bit usando Full Adder.
Prima di entrare in questo argomento, è molto importante conoscere la logica booleana e le porte logiche.
Guarda: LOGICA BOOLEANA
Guarda: PORTE LOGICHE
Guarda: FLIP FLOPS
Cos’è un Adder?
Un adder è un tipo di calcolatrice che viene usata per aggiungere due numeri binari. Quando dico calcolatrice, non intendo una con pulsanti, questa è un circuito che può essere integrato con molti altri circuiti per una vasta gamma di applicazioni. Ci sono due tipi di sommatori;
- Half adder
- Full adder
Half adder
Con l’aiuto del half adder, possiamo progettare circuiti che sono capaci di eseguire semplici addizioni con l’aiuto di porte logiche.
Diamo prima un’occhiata all’addizione di singoli bit.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Queste sono le combinazioni di singoli bit meno possibili. Ma il risultato per 1+1 è 10. Anche se questo problema può essere risolto con l’aiuto di un EXOR Gate, se ti interessa l’uscita, il risultato della somma deve essere riscritto come uscita a 2 bit.
Quindi le equazioni di cui sopra possono essere scritte come
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Qui l’uscita ‘1’di ’10’ diventa il carry-out. Il risultato è mostrato in una tabella di verità qui sotto. ‘SUM’ è l’uscita normale e ‘CARRY’ è il riporto.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Da questa equazione, è chiaro che questo sommatore a 1 bit può essere facilmente implementato con l’aiuto di EXOR Gate per l’uscita ‘SUM’ e un AND Gate per il carry. Date un’occhiata all’implementazione qui sotto.
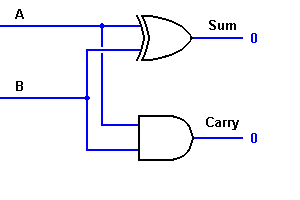
Per un’addizione complessa, ci possono essere casi in cui è necessario aggiungere due byte a 8 bit. Questo può essere fatto solo con l’aiuto della logica full-adder.
Full Adder
Questo tipo di sommatore è un po’ più difficile da implementare di un half-adder. La differenza principale tra un half-adder e un full-adder è che il full-adder ha tre ingressi e due uscite. I primi due ingressi sono A e B e il terzo ingresso è un ingresso carry designato come CIN. Quando si progetta una logica full-adder, saremo in grado di stringerne otto insieme per creare un adder largo come un byte e portare il carry bit da un adder al successivo.
Il carry in uscita è designato come COUT e l’uscita normale è designata come S. Date un’occhiata alla tabella della verità.
INGRESSI USCITE
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Dalla tabella della veritàtabella di verità, la logica dell’addizionatore completo può essere implementata. Possiamo vedere che l’uscita S è un EXOR tra l’ingresso A e l’uscita della semisomma con gli ingressi B e CIN. Dobbiamo anche notare che il COUT sarà vero solo se uno qualsiasi dei due ingressi sui tre è ALTO.
Quindi, possiamo implementare un circuito full adder con l’aiuto di due circuiti half adder. Il primo mezzo sommatore sarà utilizzato per sommare A e B per produrre una somma parziale. La seconda logica half adder può essere usata per aggiungere CIN alla Somma prodotta dal primo half adder per ottenere l’uscita finale S. Se una qualsiasi delle logiche half adder produce un riporto, ci sarà un riporto in uscita. Così, COUT sarà una funzione OR delle uscite di carry dell’half-adder. Date un’occhiata all’implementazione del circuito full adder mostrato qui sotto.
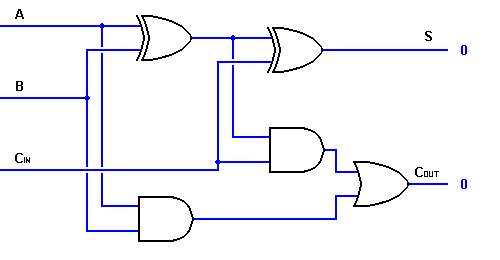
Anche se l’implementazione di diagrammi logici più grandi è possibile con la logica full adder di cui sopra, un simbolo più semplice è usato principalmente per rappresentare l’operazione. Di seguito è riportata una rappresentazione schematica più semplice di un sommatore completo a un bit.
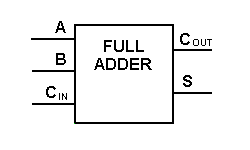
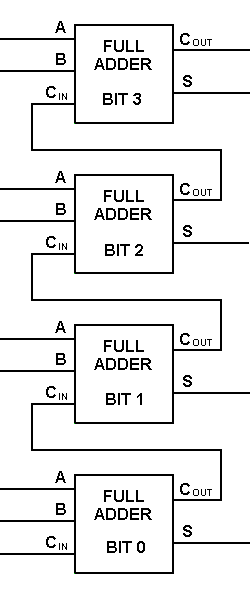
Con questo tipo di simbolo, possiamo sommare due bit prendendo un carry dal successivo ordine di grandezza inferiore, e inviando un carry al successivo ordine di grandezza superiore. In un computer, per un’operazione a più bit, ogni bit deve essere rappresentato da un sommatore completo e deve essere aggiunto simultaneamente. Così, per sommare due numeri a 8 bit, avrete bisogno di 8 sommatori completi che possono essere formati mettendo in cascata due dei blocchi a 4 bit. L’addizione di due numeri a 4 bit è mostrata qui sotto.