Iniziamo esaminando la divisione di valori con esponenti.
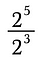
Ricordo che gli esponenti rappresentano una moltiplicazione ripetuta. Quindi possiamo riscrivere l’espressione precedente come:
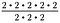
Siccome 2/2 = 1, cancella tre serie di 2/2. Questo lascia 2 – 2, o 2 al quadrato.
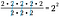
Naturalmente possiamo prendere una scorciatoia e sottrarre il numero di 2 in basso dal numero di 2 in alto. Dato che queste quantità sono rappresentate dai rispettivi esponenti, tutto quello che dobbiamo fare è scrivere la base comune con la differenza dei valori degli esponenti come potenza.
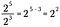
Se generalizziamo questa regola, abbiamo la seguente dove n rappresenta un numero reale non nullo e x e y sono anche numeri reali.
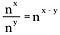
Esplorazione della potenza zero
Da qui è facile derivare la spiegazione del perché qualsiasi numero non zero elevato alla potenza zero è uguale a 1. Di nuovo, guardiamo un esempio concreto.
Sappiamo che qualsiasi numero non zero diviso per se stesso è uguale a 1. Quindi posso scrivere quanto segue:
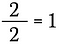
Questo è lo stesso che scrivere:
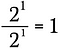
Ora utilizzerò la regola dell’esponente di cui sopra per riscrivere il lato sinistro di questa equazione.
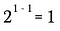
Naturalmente, questo equivale a:
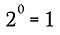
Possiamo usare lo stesso procedimento di questo esempio, insieme alla regola generalizzata di cui sopra, per dimostrare che qualsiasi numero reale non nullo elevato alla potenza zero deve dare come risultato 1.
Che mi dici di zero alla potenza zero?
Ecco dove le cose si complicano. Il metodo di cui sopra si rompe perché, ovviamente, dividere per zero è un no-no. Esaminiamo il perché.
Iniziamo guardando un comune ERRORE di divisione per zero.
Che ne dite di 2÷0? Vediamo perché non possiamo farlo.
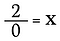
La divisione è davvero solo una forma di moltiplicazione, quindi cosa succede se riscrivo l’equazione sopra come:
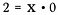
Quale valore potrebbe soddisfare questa equazione per x?
Non c’è nessun valore! Qualsiasi numero per zero dà come risultato zero, non può mai essere uguale a 2. Pertanto, diciamo che la divisione per zero è indefinita. Non c’è nessuna soluzione possibile.
Ora guardiamo 0÷0.
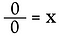
Di nuovo, riscriviamolo come un problema di moltiplicazione.
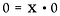
Qui incontriamo una situazione molto diversa. La soluzione di x potrebbe essere QUALSIASI numero reale! Non c’è modo di determinare quale sia x. Quindi, 0/0 è considerato indeterminato*, non indefinito.
Se proviamo ad usare il metodo precedente con zero come base per determinare quale sarebbe lo zero alla potenza zero, ci fermiamo immediatamente e non possiamo continuare perché sappiamo che 0÷0 ≠ 1, ma è indeterminato.
Quindi a cosa equivale lo zero alla potenza zero? Alcuni credono che dovrebbe essere definito come 1 mentre altri pensano che sia 0, e alcuni credono che sia indefinito. Ci sono buoni argomenti matematici per ciascuno, e forse è più correttamente considerato indeterminato.
Nonostante questo, la comunità matematica è favorevole a definire lo zero alla potenza zero come 1, almeno per la maggior parte degli scopi.
Per il matematico dilettante, una definizione utile degli esponenti è la seguente: