Prequisito – Misure di distanza nel Data Mining
Nel Data Mining, la misura di similarità si riferisce alla distanza con dimensioni che rappresentano caratteristiche dell’oggetto dei dati, in un set di dati. Se questa distanza è minore, ci sarà un alto grado di somiglianza, ma quando la distanza è grande, ci sarà un basso grado di somiglianza.
Alcune delle misure di somiglianza popolari sono –
- Distanza Euclidea.
- Distanza Manhattan.
- Simiglianza Jaccard.
- Distanza Minkowski.
- Simiglianza Cosina.
Simiglianza Cosina è una metrica, utile per determinare, quanto sono simili gli oggetti dati indipendentemente dalla loro dimensione. Possiamo misurare la somiglianza tra due frasi in Python usando la somiglianza del coseno. Nella somiglianza del coseno, gli oggetti di dati in un set di dati sono trattati come un vettore. La formula per trovare la similarità del coseno tra due vettori è –
Cos(x, y) = x . y / ||x|| * ||y||
dove,
- x . y = prodotto (punto) dei vettori ‘x’ e ‘y’.
- ||x||| e ||y||| = lunghezza dei due vettori ‘x’ e ‘y’.
- ||x||| * ||y|| = prodotto incrociato dei due vettori ‘x’ e ‘y’.
Esempio :
Considera un esempio per trovare la similarità tra due vettori – ‘x’ e ‘y’, usando la Similarità del Coseno.
Il vettore ‘x’ ha valori, x = { 3, 2, 0, 5 }
Il vettore ‘y’ ha valori, y = { 1, 0, 0, 0 }
La formula per calcolare la similarità del coseno è : Cos(x, y) = x . y / ||x|| * ||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
La dissomiglianza tra i due vettori ‘x’ e ‘y’ è data da –
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- La somiglianza coseno tra due vettori si misura in ‘θ’.
- Se θ = 0°, i vettori ‘x’ e ‘y’ si sovrappongono, dimostrando così che sono simili.
- Se θ = 90°, i vettori ‘x’ e ‘y’ sono dissimili.
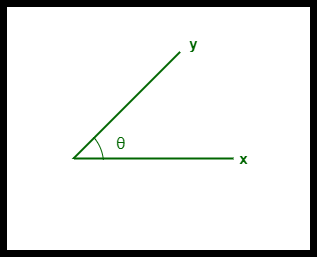
Simiglianza coseno tra due vettori
Simiglianza coseno :
- La similitudine coseno è vantaggiosa perché anche se i due oggetti dati simili sono lontani dalla distanza euclidea a causa delle dimensioni, potrebbero ancora avere un angolo minore tra loro. Più piccolo è l’angolo, più alta è la somiglianza.
- Quando è tracciata su uno spazio multidimensionale, la somiglianza del coseno cattura l’orientamento (l’angolo) degli oggetti dati e non la grandezza.