Fisica

La fissione nucleare è una reazione in cui un nucleo viene scisso (o fessurato). La fissione controllata è una realtà, mentre la fusione controllata è una speranza per il futuro. Centinaia di centrali a fissione nucleare in tutto il mondo attestano che la fissione controllata è pratica e, almeno a breve termine, economica, come si vede nella figura 1. Mentre l’energia nucleare è stata di scarso interesse per decenni dopo TMI e Chernobyl (e ora Fukushima Daiichi), la crescente preoccupazione per il riscaldamento globale ha riportato l’energia nucleare sul tavolo come una valida alternativa energetica. Alla fine del 2009, c’erano 442 reattori in funzione in 30 paesi, che forniscono il 15% dell’elettricità mondiale. La Francia fornisce più del 75% della sua elettricità con l’energia nucleare, mentre gli Stati Uniti hanno 104 reattori operativi che forniscono il 20% della loro elettricità. L’Australia e la Nuova Zelanda non ne hanno nessuno. La Cina sta costruendo centrali nucleari al ritmo di una partenza al mese.

Figura 1. Le persone che vivono vicino a questa centrale nucleare non hanno un’esposizione misurabile alle radiazioni riconducibili alla centrale. Circa il 16% dell’energia elettrica mondiale è generata dalla fissione nucleare controllata in tali impianti. Le torri di raffreddamento sono le caratteristiche più evidenti, ma non sono uniche per l’energia nucleare. Il reattore è nel piccolo edificio a cupola a sinistra delle torri. (credit: Kalmthouts)

La fissione è l’opposto della fusione e rilascia energia solo quando i nuclei pesanti vengono divisi. Come notato in Fusione, l’energia viene rilasciata se i prodotti di una reazione nucleare hanno una maggiore energia di legame per nucleone (BE/A) rispetto ai nuclei genitori. La figura 2 mostra che il BE/A è maggiore per i nuclei di media massa rispetto ai nuclei pesanti, il che implica che quando un nucleo pesante viene scisso, i prodotti hanno meno massa per nucleone, quindi quella massa viene distrutta e viene rilasciata energia nella reazione. La quantità di energia per reazione di fissione può essere grande, anche per gli standard nucleari. Il grafico in figura 2 mostra che BE/A è circa 7,6 MeV/nucleone per i nuclei più pesanti (A circa 240), mentre BE/A è circa 8,6 MeV/nucleone per i nuclei con A circa 120. Quindi, se un nucleo pesante si divide a metà, viene rilasciato circa 1 MeV per nucleone, o circa 240 MeV per fissione. Questo è circa 10 volte l’energia per reazione di fusione, e circa 100 volte l’energia del decadimento medio α, β o γ.

Esempio 1. Calcolo dell’energia rilasciata dalla fissione

Calcolare l’energia rilasciata nella seguente reazione di fissione spontanea:

238U → 95Sr + 140Xe + 3n

data la massa atomica di m(238U) = 238.050784 u, m(95Sr) = 94.919388 u, m(140Xe) = 139.921610 u, e m(n) =1.008665 u.

Strategia

Come sempre, l’energia rilasciata è uguale alla massa distrutta per c2, quindi dobbiamo trovare la differenza di massa tra il 238U genitore e i prodotti di fissione.

Soluzione

I prodotti hanno una massa totale di

{begin{array}{lll}{m}_{\testo{prodotti}}& =& 94.919388{ u}+139.921610 \testo{ u}+3\sinistra(1.008665{ u}destra)\ & =& 237.La massa persa è la massa di 238U meno mprodotti, ovvero

Δm = 238,050784 u- 237,8669933 u = 0.183791 u,

quindi l’energia rilasciata è

Discussione

In questo esempio emergono diverse cose importanti. L’energia di 171 MeV rilasciata è grande, ma un po’ meno dei 240 MeV stimati in precedenza. Questo perché questa reazione di fissione produce neutroni e non divide il nucleo in due parti uguali. La fissione di un dato nuclide, come il 238U , non produce sempre gli stessi prodotti. La fissione è un processo statistico in cui un’intera gamma di prodotti sono prodotti con varie probabilità. La maggior parte della fissione produce neutroni, anche se il numero varia con ogni fissione. Questo è un aspetto estremamente importante della fissione, perché i neutroni possono indurre altre fissioni, permettendo reazioni a catena autosostenute.

La fissione spontanea può verificarsi, ma di solito non è la modalità di decadimento più comune per un dato nuclide. Per esempio, il 238U può fissionare spontaneamente, ma decade principalmente per emissione α. La fissione indotta dai neutroni è cruciale, come si vede nella figura 2. Essendo senza carica, anche i neutroni a bassa energia possono colpire un nucleo ed essere assorbiti una volta che sentono la forza nucleare attrattiva. I grandi nuclei sono descritti da un modello di goccia liquida con tensione superficiale e modalità di oscillazione, perché il gran numero di nucleoni si comporta come gli atomi in una goccia. Il neutrone è attratto e quindi deposita energia, causando la deformazione del nucleo come una goccia liquida. Se allungato abbastanza, il nucleo si restringe al centro. Il numero di nucleoni in contatto e la forza della forza nucleare che lega il nucleo si riducono. La repulsione coulombiana tra le due estremità riesce allora a fissionare il nucleo, che scoppia come una goccia d’acqua in due grandi pezzi e qualche neutrone. La fissione indotta dai neutroni può essere scritta come

n + AX → FF1 + FF2 + xn,

dove FF1 e FF2 sono i due nuclei figli, chiamati frammenti di fissione, e x è il numero di neutroni prodotti. Il più delle volte, le masse dei frammenti di fissione non sono le stesse. La maggior parte dell’energia rilasciata va nell’energia cinetica dei frammenti di fissione, mentre il resto va nei neutroni e negli stati eccitati dei frammenti. Poiché i neutroni possono indurre la fissione, è possibile una reazione a catena autosostenuta, a condizione che più di un neutrone sia prodotto in media – cioè, se x>1 in n + AX → FF1 + FF2 + xn. Questo può essere visto anche nella Figura 3. Un esempio di una tipica reazione di fissione indotta da neutroni è

n+{}_{{text{92}}^{{text{235}{U} a {}_{text{56}^{{text{142}}{text{Ba}+{}_{text{36}}^{text{91}{Kr}+3{text{n}.

Nota che in questa equazione, la carica totale rimane la stessa (è conservata): 92 + 0 = 56 + 36. Inoltre, per quanto riguarda i numeri interi, la massa è costante: 1 + 235 = 142 + 91 + 3. Questo non è vero quando consideriamo le masse fino a 6 o 7 punti significativi, come nell’esempio precedente.

Figura 2. Viene mostrata la fissione indotta da neutroni. In primo luogo, l’energia è messa in questo grande nucleo quando assorbe un neutrone. Agendo come una goccia di liquido colpita, il nucleo si deforma e comincia a restringersi al centro. Poiché meno nucleoni sono in contatto, la forza repulsiva di Coulomb è in grado di rompere il nucleo in due parti con alcuni neutroni che volano via.

Figura 3. Una reazione a catena può produrre una fissione autosostenuta se ogni fissione produce abbastanza neutroni da indurre almeno un’altra fissione. Questo dipende da diversi fattori, incluso quanti neutroni sono prodotti in una fissione media e quanto è facile far fissionare un particolare tipo di nuclide.

Non ogni neutrone prodotto dalla fissione induce la fissione. Alcuni neutroni sfuggono al materiale fissionabile, mentre altri interagiscono con un nucleo senza farlo fissionare. Possiamo aumentare il numero di fissioni prodotte dai neutroni avendo una grande quantità di materiale fissionabile. La quantità minima necessaria per la fissione autosostenuta di un dato nuclide è chiamata massa critica. Alcuni nuclidi, come il 239Pu, producono più neutroni per fissione di altri, come il 235U . Inoltre, alcuni nuclidi sono più facili da far fissionare di altri. In particolare, 235U e 239Pu, sono più facili da fissionare rispetto al molto più abbondante 238U. Entrambi i fattori influenzano la massa critica, che è più piccola per il 239Pu.

La ragione per cui 235U e 239Pu sono più facili da fissionare che 238U è che la forza nucleare è più attraente per un numero pari di neutroni in un nucleo che per un numero dispari. Considera che {_{text{92}}^{235}}{{text{U}}_{143}} ha 143 neutroni, e {_{text{94}^{text{239}{{P}}_{text{145}} ha 145 neutroni, mentre {_{text{92}}^{text{238}{{text{146}} ha 146. Quando un neutrone incontra un nucleo con un numero dispari di neutroni, la forza nucleare è più attraente, perché il neutrone addizionale rende il numero pari. Circa 2 MeV di energia in più si depositano nel nucleo risultante rispetto a quanto accadrebbe se il numero di neutroni fosse già pari. Questa energia extra produce una maggiore deformazione, rendendo la fissione più probabile. Così, 235U e 239Pu sono combustibili da fissione superiori. L’isotopo 235U è solo lo 0,72% dell’uranio naturale, mentre il 238U è il 99,27%, e il 239Pu non esiste in natura. L’Australia ha i maggiori depositi di uranio nel mondo, con il 28% del totale. È seguita dal Kazakistan e dal Canada. Gli Stati Uniti hanno solo il 3% delle riserve globali.

La maggior parte dei reattori a fissione utilizzano 235U, che viene separato dal 238U con una certa spesa. Questo è chiamato arricchimento. Il metodo di separazione più comune è la diffusione gassosa di esafluoruro di uranio (UF6) attraverso membrane. Poiché il 235U ha meno massa del 238U, le sue molecole di UF6 hanno una velocità media più alta alla stessa temperatura e si diffondono più velocemente. Un’altra caratteristica interessante del 235U è che assorbe preferenzialmente neutroni molto lenti (con energie di una frazione di eV), mentre le reazioni di fissione producono neutroni veloci con energie dell’ordine di un MeV. Per realizzare un reattore a fissione autosostenuto con 235U , è quindi necessario rallentare (“termalizzare”) i neutroni. L’acqua è molto efficace, poiché i neutroni si scontrano con i protoni nelle molecole d’acqua e perdono energia. La figura 4 mostra uno schema di un progetto di reattore, chiamato reattore ad acqua pressurizzata.

Figura 4. Un reattore ad acqua pressurizzata è abilmente progettato per controllare la fissione di grandi quantità di 235U, mentre usa il calore prodotto nella reazione di fissione per creare vapore per generare energia elettrica. Le barre di controllo regolano il flusso di neutroni in modo che la criticità sia ottenuta, ma non superata. Nel caso in cui il reattore si surriscaldi e faccia bollire l’acqua, la reazione a catena termina, perché l’acqua è necessaria per termalizzare i neutroni. Questa caratteristica di sicurezza intrinseca può essere superata in circostanze estreme.

Le barre di controllo contenenti nuclidi che assorbono molto fortemente i neutroni sono usate per regolare il flusso di neutroni. Per produrre grande potenza, i reattori contengono da centinaia a migliaia di masse critiche, e la reazione a catena si autoalimenta facilmente, una condizione chiamata criticità. Il flusso di neutroni deve essere attentamente regolato per evitare un aumento esponenziale delle fissioni, una condizione chiamata supercriticità. Le barre di controllo aiutano a prevenire il surriscaldamento, forse anche una fusione o uno smontaggio esplosivo. L’acqua che è usata per termalizzare i neutroni, necessari per farli indurre la fissione in 235U, e raggiungere la criticità, fornisce un feedback negativo per gli aumenti di temperatura. Nel caso in cui il reattore si surriscaldi e faccia bollire l’acqua in vapore o venga violato, l’assenza di acqua uccide la reazione a catena. Un calore considerevole, tuttavia, può ancora essere generato dai prodotti radioattivi di fissione del reattore. Altre caratteristiche di sicurezza, quindi, devono essere incorporate in caso di incidente con perdita di refrigerante, tra cui acqua di raffreddamento ausiliaria e pompe.

Un nuclide già menzionato è il 239Pu, che ha un’emivita di 24.120 anni e non esiste in natura. Il plutonio-239 è prodotto dal 238U nei reattori, e fornisce un’opportunità per utilizzare l’altro 99% di uranio naturale come fonte di energia. La seguente sequenza di reazione, chiamata breeding, produce il 239Pu. L’allevamento inizia con la cattura di neutroni da parte del 238U :

L’uranio-239 decade poi β-:

239U → 239Np + β- + ve(t1/2 = 23 min).

Il nettunio-239 decade anche β-:

239Np → 239Pu + β- + ve(t1/2 = 2,4 d).

Il plutonio-239 si accumula nel combustibile del reattore ad un tasso che dipende dalla probabilità di cattura dei neutroni da parte del 238U (tutto il combustibile del reattore contiene più 238U che 235U). I reattori progettati specificamente per produrre plutonio sono chiamati reattori breeder. Sembrano essere intrinsecamente più pericolosi dei reattori convenzionali, ma non si sa se i loro rischi possano essere resi economicamente accettabili. I quattro reattori di Chernobyl, compreso quello che è stato distrutto, sono stati costruiti per fabbricare plutonio e produrre elettricità. Questi reattori avevano un design significativamente diverso dal reattore ad acqua pressurizzata illustrato sopra. Il plutonio-239 ha dei vantaggi rispetto al 235U come combustibile per reattori – produce in media più neutroni per fissione, ed è più facile che un neutrone termico lo faccia fissionare. È anche chimicamente diverso dall’uranio, quindi è intrinsecamente più facile da separare dal minerale di uranio. Questo significa che il 239Pu ha una massa critica particolarmente piccola, un vantaggio per le armi nucleari.

PhET Explorations: Fissione nucleare

Avviare una reazione a catena, o introdurre isotopi non radioattivi per prevenirne una. Controlla la produzione di energia in un reattore nucleare!

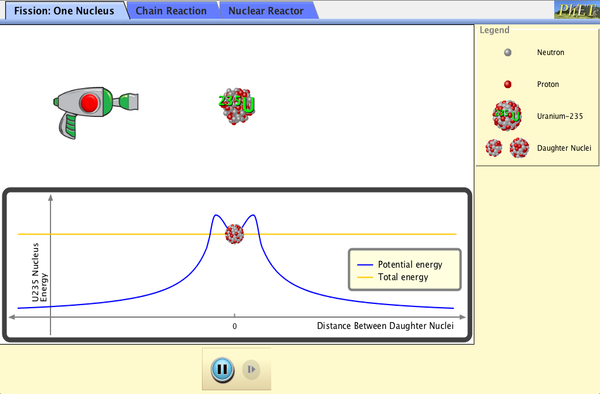
Clicca per scaricare la simulazione. Esegui usando Java.

Riassunto della sezione

• La fissione nucleare è una reazione in cui un nucleo si divide.
• La fissione rilascia energia quando nuclei pesanti si dividono in nuclei di media massa.
• La fissione autosostenuta è possibile, perché la fissione indotta da neutroni produce anche neutroni che possono indurre altre fissioni, n + AX → FF1 + FF2 + xn, dove FF1 e FF2 sono i due nuclei figli, o frammenti di fissione, e x è il numero di neutroni prodotti.
• Una massa minima, chiamata massa critica, deve essere presente per raggiungere la criticità.
• Più di una massa critica può produrre supercriticità.
• La produzione di nuovi o diversi isotopi (specialmente 239Pu) tramite trasformazione nucleare è chiamata breeding, e i reattori progettati per questo scopo sono chiamati reattori breeder.