La quarta elementare Alice chiede: “Quante diagonali ci sono in un decagono?”
Grande domanda, Alice. Ma invece di darti una risposta a questa domanda, ti mostrerò come puoi scoprirlo da sola. E non solo, ti mostrerò come puoi capire la risposta per qualsiasi poligono, anche se ha 20, o 50, o 2000 lati!
Pronto? Cominciamo con un semplice esempio. Andremo con un poligono che ha 8 lati (che è chiamato ottagono), come questo:
Ora, questo poligono, poiché ha otto lati, ha anche otto vertici. Sembra un po’ opprimente cercare di capire tutte le diagonali, quindi concentriamoci solo su un vertice. Quante diagonali puoi disegnare in un ottagono, che iniziano tutte da un vertice?
La risposta a questa domanda è cinque. Dai un’occhiata al diagramma qui sotto:

In questo diagramma ho scelto la diagonale a sinistra appena sotto il vertice superiore, e ho disegnato diagonali verso ogni vertice a cui posso disegnare una diagonale. Su quali diagonali non posso disegnare diagonali? Beh, non posso disegnare una diagonale da un vertice verso se stesso, e non posso disegnare diagonali verso i due vertici accanto a quello (perché quelle non sarebbero diagonali; sarebbero lati!).
Quindi ci sono tre vertici a cui non posso disegnare diagonali da quel vertice. Otto vertici in totale, meno i tre a cui non posso disegnare, rimangono cinque. Questo è importante da ricordare: sottrai 3 dal numero di vertici, e hai il numero di diagonali che puoi disegnare da qualsiasi vertice.
Ma quello è solo un vertice! Potresti disegnare diagonali da qualsiasi vertice, giusto? Certo! E ci sono otto vertici nel nostro ottagono, quindi prendiamo il numero di diagonali per vertice, e lo moltiplichiamo per il numero di vertici: 5 x 8 = 40.
Si potrebbe essere tentati di pensare che questa sia la nostra risposta, ma non lo è. Perché no? Perché abbiamo contato ogni diagonale due volte! Ogni diagonale ha due vertici, quindi l’abbiamo contata da un’estremità, e l’abbiamo contata anche dall’altra estremità. Quindi, per ottenere il numero effettivo di diagonali, dobbiamo dividere la nostra risposta per 2. 40 / 2 = 20. Ci sono venti diagonali in un ottagono.
Proviamo questo ragionamento su un poligono che ha 2000 lati. Ora, non ho intenzione di disegnare un poligono da 2000 lati per te; dovremo solo elaborare il ragionamento senza un’immagine.
- Scegli un vertice. Quante diagonali puoi disegnare da quel vertice? Risposta: 2000 – 3 = 1997.
- Quanti vertici in totale? Risposta: 2000
- Quante diagonali contate da tutti i vertici? Risposta: 1997 x 2000 = 3.994.000
- Ops! Abbiamo contato ogni diagonale due volte! Come ci sbarazziamo dei duplicati? Risposta: 3994000 / 2 = 1.997.000
Così un 2000-gon ha 1.997.000 diagonali!
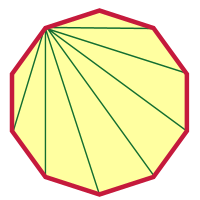
Dopo aver fatto qualcosa di così folle come un 2000-gon, un decagono non dovrebbe sembrare così difficile, giusto? Io ti faccio iniziare e tu puoi finire da qui. Ho scelto un vertice e ho disegnato le diagonali da quel vertice.
Quante sono? Sei stato in grado di capire quanti erano senza guardare l’immagine?
Riesci a capirlo da qui? Spero di sì! Buona fortuna, Alice.
A proposito, c’è una formula che puoi usare; assomiglia a questa: D = n(n – 3)/2. Ma onestamente, non mi aspetto che i miei studenti la memorizzino. Mi aspetto che ricordino come ragioniamo qui. Se capite la logica, è anche meglio che avere una formula!