Non capita spesso che un’equazione matematica finisca sulla stampa nazionale, né tanto meno nella radio popolare o, cosa più sorprendente di tutte, sia oggetto di un dibattito nel Parlamento britannico. Tuttavia, nel 2003 la buona vecchia equazione quadratica, che tutti abbiamo imparato a scuola, era tutte queste cose.
Da dove cominciamo

Tutto è iniziato in una riunione dell’Unione Nazionale degli Insegnanti. L’equazione quadratica fu tenuta in alto davanti alla nazione come esempio della crudele tortura inflitta dai matematici ai poveri ignari scolari. Incuriosita da questa accusa, l’equazione quadratica accettò un ruolo da protagonista alla radio in prima serata dove fu interrogata da un formidabile intervistatore più abituato a sfidare il primo ministro. Il Times (di Londra) ha preso spazio nella sua colonna dei leader, di solito riservata a discussioni pesanti sulla salute morale (o meno) del mondo moderno, per proclamare che l’equazione quadratica era inutile, la matematica era inutile e che nessuno voleva studiare la matematica, quindi perché preoccuparsi. Preoccupati che pericolose ammissioni dell’equazione quadratica rimanessero incontrastate, l’importanza vitale dell’equazione per la sopravvivenza del Regno Unito è stata discussa (è stata presa una posizione positiva, sarete felici di saperlo) nella Camera dei Comuni britannica.
Dove sarebbe finito tutto questo? L’equazione quadratica era davvero morta? A qualcuno importava? I matematici sono davvero dei mostri malvagi che vogliono solo infliggere equazioni quadratiche alle nuove generazioni come mezzo per corrompere le loro anime immortali?
Forse sì, ma non è davvero colpa dell’equazione quadratica. Infatti, l’equazione quadratica ha giocato un ruolo fondamentale non solo nell’intera civiltà umana come la conosciamo, ma nella possibile individuazione di altre civiltà aliene e persino in attività moderne vitali come guardare la televisione satellitare. Cos’altro, a parte la natura della rivelazione divina, si potrebbe considerare che abbia avuto un tale impatto sulla vita come la conosciamo? In effetti, in un senso molto reale, le equazioni quadratiche possono salvarti la vita.
I Babilonesi
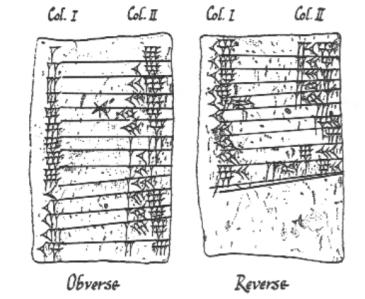
Le tavolette cuneiformi babilonesi che registrano le 9 tavole dei tempi
Tutto è iniziato intorno al 3000 a.C. con i Babilonesi. Erano una delle prime civiltà del mondo, e hanno sviluppato alcune grandi idee come l’agricoltura, l’irrigazione e la scrittura. Tracciarono i percorsi del sole, della luna e dei pianeti e li registrarono su tavolette d’argilla (che si possono ancora vedere al British Museum). Ai Babilonesi dobbiamo le idee moderne di angolo, compreso il modo in cui il cerchio è diviso in 360 gradi (a causa di un piccolo errore di calcolo, uno al giorno). Siamo anche in debito con i Babilonesi per l’invenzione piuttosto meno piacevole del (temuto) uomo delle tasse. E questo era uno dei motivi per cui i babilonesi avevano bisogno di risolvere equazioni quadratiche.
Immaginiamo che tu sia un contadino babilonese. Da qualche parte nella tua fattoria hai un campo quadrato su cui coltivi qualche raccolto. Quale quantità del tuo raccolto puoi coltivare sul campo? Raddoppiate la lunghezza di ogni lato del campo e scoprirete che potete coltivare quattro volte tanto il raccolto di prima. La ragione di questo è che la quantità di raccolto che puoi coltivare è proporzionale all’area del campo, che è a sua volta proporzionale al quadrato della lunghezza del lato. In termini matematici, se  è la lunghezza del lato del campo,
è la lunghezza del lato del campo, 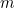 è la quantità di raccolto che si può coltivare su un campo quadrato di lunghezza laterale 1, e
è la quantità di raccolto che si può coltivare su un campo quadrato di lunghezza laterale 1, e  è la quantità di raccolto che si può coltivare, allora
è la quantità di raccolto che si può coltivare, allora
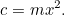 |
Questa è la nostra prima equazione quadratica, nuda e lampeggiante alla luce del sole. Le equazioni quadratiche e le aree sono legate come fratelli e sorelle nella stessa famiglia. Tuttavia, al momento non dobbiamo risolvere nulla – finché non arriva l’uomo delle tasse, cioè! Allegramente dice al contadino: “Voglio che tu mi dia raccolti per pagare le tasse sulla tua fattoria”. Il contadino ora ha un dilemma: quanto grande è il campo di cui ha bisogno per coltivare quella quantità di raccolto? Noi possiamo rispondere facilmente a questa domanda, infatti
raccolti per pagare le tasse sulla tua fattoria”. Il contadino ora ha un dilemma: quanto grande è il campo di cui ha bisogno per coltivare quella quantità di raccolto? Noi possiamo rispondere facilmente a questa domanda, infatti
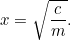 |
Trovare le radici quadrate con una calcolatrice è facile per noi, ma era più un problema per i Babilonesi. Infatti hanno sviluppato un metodo di approssimazione successiva alla risposta che è identico all’algoritmo (chiamato metodo Newton-Raphson) usato dai computer moderni per risolvere problemi molto più difficili delle equazioni quadratiche.
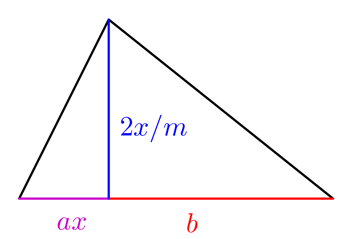
Ora, non tutti i campi sono quadrati. Supponiamo ora che l’agricoltore abbia un campo di forma più strana con due sezioni triangolari come mostrato sulla destra.
Per valori appropriati di  e
e 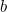 la quantità di raccolto che il contadino può coltivare in questo campo è data da
la quantità di raccolto che il contadino può coltivare in questo campo è data da
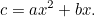 |
Questo sembra molto più simile all’equazione quadratica a cui siamo abituati, e anche sotto l’occhio malefico dell’uomo delle tasse, è molto più difficile da risolvere. Eppure i babilonesi hanno trovato di nuovo la risposta. Prima dividiamo per  per dare
per dare
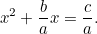 |
Ora completiamo il quadrato usando il fatto che
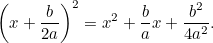 |
Combinando questo con l’equazione originale abbiamo
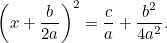 |
Questa è ora un’equazione che possiamo risolvere prendendo radici quadrate. Il risultato è la famosa “formula 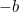 “:
“:
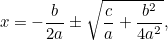 |
che può essere riscritta come
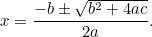 |
(La formula di solito ha “-4ac” perché l’equazione quadratica è più spesso scritta nella forma “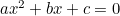 “.)
“.)
Il fatto che prendere una radice quadrata può dare una risposta positiva o negativa porta al notevole risultato che un’equazione quadratica ha due soluzioni. Alla faccia dei puzzle matematici che hanno solo una soluzione!
Ora, è qui che l’insegnamento delle equazioni quadratiche spesso si ferma. Abbiamo raggiunto quell’oggetto amato da tutti i giornalisti quando intervistano i matematici: una formula. Si possono inventare infinite domande che prevedono di mettere i valori di 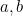 e
e  nella formula per dare (due) risposte. Ma la matematica non è affatto questo. Trovare una formula è solo il primo passo di una lunga strada. Dobbiamo chiederci: cosa significa la formula; cosa ci dice dell’universo; avere una formula è davvero importante? Vediamo ora dove ci porterà questa formula.
nella formula per dare (due) risposte. Ma la matematica non è affatto questo. Trovare una formula è solo il primo passo di una lunga strada. Dobbiamo chiederci: cosa significa la formula; cosa ci dice dell’universo; avere una formula è davvero importante? Vediamo ora dove ci porterà questa formula.
Una sorpresa per i greci, un po’ di origami matematico e il senso delle proporzioni
Ora andiamo avanti di 1000 anni fino agli antichi greci e vediamo cosa hanno fatto delle equazioni quadratiche. I greci erano matematici superbi e scoprirono molta della matematica che usiamo ancora oggi. Una delle equazioni che erano interessati a risolvere era la (semplice) equazione quadratica
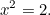 |

Loro sapevano che questa equazione aveva una soluzione. Infatti è la lunghezza dell’ipotenusa di un triangolo rettangolo che ha i lati di lunghezza uno.
Dal teorema di Pitagora segue che se un triangolo rettangolotriangolo rettangolo ha i lati minori  e
e  e l’ipotenusa
e l’ipotenusa  allora
allora
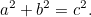 |
mettendo 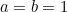 e
e  allora
allora 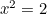 . Così
. Così 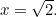
Allora, cos’è  in questo caso? O, per fare la domanda che si ponevano i greci, che tipo di numero è? La ragione per cui questo era importante risiedeva nel senso delle proporzioni dei greci. Credevano che tutti i numeri fossero in proporzione tra loro. Per essere precisi, questo significava che tutti i numeri erano frazioni della forma
in questo caso? O, per fare la domanda che si ponevano i greci, che tipo di numero è? La ragione per cui questo era importante risiedeva nel senso delle proporzioni dei greci. Credevano che tutti i numeri fossero in proporzione tra loro. Per essere precisi, questo significava che tutti i numeri erano frazioni della forma 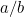 dove
dove  e
e  sono numeri interi. Numeri come 1/2, 3/4 e 355/113 sono tutti esempi di frazioni. Era naturale aspettarsi che anche
sono numeri interi. Numeri come 1/2, 3/4 e 355/113 sono tutti esempi di frazioni. Era naturale aspettarsi che anche  fosse una frazione. L’enorme sorpresa è stata che non lo è. Infatti
fosse una frazione. L’enorme sorpresa è stata che non lo è. Infatti
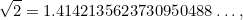 |
dove i punti  significano che l’espansione decimale di
significano che l’espansione decimale di  continua all’infinito senza alcun modello distinguibile. (
continua all’infinito senza alcun modello distinguibile. (
 fu il primo numero irrazionale (cioè un numero che non è una frazione o razionale) ad essere riconosciuto come tale. Altri esempi sono
fu il primo numero irrazionale (cioè un numero che non è una frazione o razionale) ad essere riconosciuto come tale. Altri esempi sono 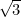 ,
,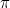 ,
,  e di fatto la “maggior parte” dei numeri. Ci è voluto fino al XIX secolo prima di avere un buon modo di pensare a questi numeri. La scoperta che
e di fatto la “maggior parte” dei numeri. Ci è voluto fino al XIX secolo prima di avere un buon modo di pensare a questi numeri. La scoperta che  non era un numero razionale causò sia grande eccitazione (100 buoi furono sacrificati come risultato) che grande shock, con lo scopritore che dovette suicidarsi. (Che questo sia un terribile avvertimento per i matematici appassionati!) A questo punto i greci abbandonarono l’algebra e si rivolsero alla geometria.
non era un numero razionale causò sia grande eccitazione (100 buoi furono sacrificati come risultato) che grande shock, con lo scopritore che dovette suicidarsi. (Che questo sia un terribile avvertimento per i matematici appassionati!) A questo punto i greci abbandonarono l’algebra e si rivolsero alla geometria.
Lontano dall’essere un numero oscuro, incontriamo  regolarmente: ogni volta che usiamo un pezzo di carta A4. In Europa, le dimensioni della carta sono misurate in formati A, dove il formato A0 è il più grande con una superficie di
regolarmente: ogni volta che usiamo un pezzo di carta A4. In Europa, le dimensioni della carta sono misurate in formati A, dove il formato A0 è il più grande con una superficie di 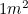 . I formati A hanno una relazione speciale tra loro. Se ora facciamo un po’ di origami, prendendo un foglio di carta A1 e piegandolo a metà (lungo il lato più lungo), otteniamo la carta A2. Piegandolo di nuovo a metà otteniamo A3, e di nuovo A4, ecc. Tuttavia, la carta è progettata in modo che le proporzioni di ciascuna delle dimensioni A siano le stesse – cioè, ogni pezzo di carta ha la stessa forma.
. I formati A hanno una relazione speciale tra loro. Se ora facciamo un po’ di origami, prendendo un foglio di carta A1 e piegandolo a metà (lungo il lato più lungo), otteniamo la carta A2. Piegandolo di nuovo a metà otteniamo A3, e di nuovo A4, ecc. Tuttavia, la carta è progettata in modo che le proporzioni di ciascuna delle dimensioni A siano le stesse – cioè, ogni pezzo di carta ha la stessa forma.
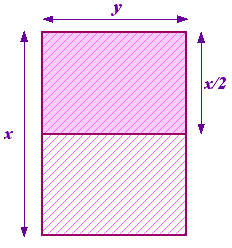
Possiamo porci il problema di quale proporzione sia questa. Inizia con un pezzo di carta con i lati x e y con x il lato più lungo. Ora dividiamo questo in due per dare un altro pezzo di carta con lati y e x/2 con y che ora è il lato più lungo. Questo è illustrato a destra.
Le proporzioni del primo pezzo di carta sono 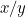 e quelle del secondo sono
e quelle del secondo sono 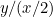 o
o 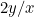 . Vogliamo che queste due proporzioni siano uguali. Questo significa che
. Vogliamo che queste due proporzioni siano uguali. Questo significa che
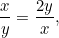 |
o
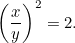 |
Un’altra equazione quadratica! Fortunatamente è una che abbiamo già incontrato. Risolvendola troviamo che
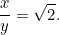 |
Questo risultato è facile da controllare. Basta prendere un foglio di carta A4 (o A3 o A5) e misurare i lati. Possiamo anche calcolare la dimensione di ogni foglio. L’area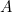 di un pezzo di carta A0 è data da
di un pezzo di carta A0 è data da
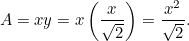 |
Ma sappiamo che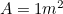 quindi abbiamo un’altra equazione quadratica per il lato più lungo
quindi abbiamo un’altra equazione quadratica per il lato più lungo di A0, data da
di A0, data da
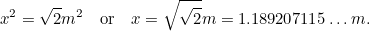 |
Questo significa che il lato più lungo di A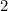 è dato da
è dato da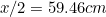 (perché?) e quello di A
(perché?) e quello di A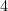 da
da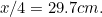 . Controllate questi dati sui vostri fogli di carta.
. Controllate questi dati sui vostri fogli di carta.
La carta usata negli Stati Uniti, chiamata foolscap, ha una proporzione diversa. Per vedere perché, torniamo ai greci e ad un’altra equazione quadratica. Dopo aver causato tanto dolore, l’equazione quadratica si riscatta nella ricerca delle proporzioni perfette: una ricerca che continua ancora oggi nella progettazione dei set cinematografici, e si può vedere in molti aspetti della natura.
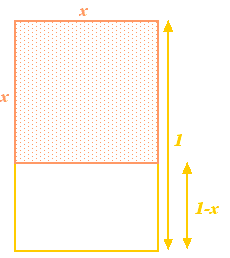
Partiamo da un rettangolo, e poi togliamo da esso un quadrato con la stessa lunghezza del lato più corto del rettangolo. Se il lato più lungo del rettangolo ha lunghezza 1 e il lato più corto ha lunghezza  , allora il quadrato ha i lati di lunghezza
, allora il quadrato ha i lati di lunghezza  . Togliendolo dal rettangolo si ottiene un rettangolo più piccolo con lato più lungo
. Togliendolo dal rettangolo si ottiene un rettangolo più piccolo con lato più lungo  e lato più piccolo
e lato più piccolo 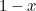 . Fin qui, tutto astratto. Tuttavia, i greci credevano che il rettangolo che aveva le proporzioni più estetiche (il cosiddetto Rettangolo d’oro) era quello per cui il rettangolo grande e quello piccolo costruiti sopra avevano le stesse proporzioni. Perché questo sia possibile dobbiamo avere
. Fin qui, tutto astratto. Tuttavia, i greci credevano che il rettangolo che aveva le proporzioni più estetiche (il cosiddetto Rettangolo d’oro) era quello per cui il rettangolo grande e quello piccolo costruiti sopra avevano le stesse proporzioni. Perché questo sia possibile dobbiamo avere
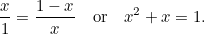 |
Questa è un’altra equazione quadratica: una molto importante che si presenta in ogni tipo di applicazione. Ha la soluzione (positiva)
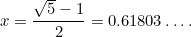 |
Il numero  è chiamato rapporto aureo ed è spesso indicato dalla lettera greca
è chiamato rapporto aureo ed è spesso indicato dalla lettera greca 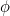 .
.

Il rettangolo d’oro può essere visto nella forma delle finestre, specialmente sulle case georgiane. Più recentemente, il Rapporto Aureo può anche essere trovato come la “forma perfetta” per le fotografie e le immagini dei film. L’equazione quadratica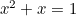 si presenta anche negli studi sulle popolazioni di conigli e nel modello in cui sono disposti i semi dei girasoli e le foglie sui fusti delle piante. Tutti questi sono collegati al rapporto aureo attraverso la sequenza di Fibonacci che è data da
si presenta anche negli studi sulle popolazioni di conigli e nel modello in cui sono disposti i semi dei girasoli e le foglie sui fusti delle piante. Tutti questi sono collegati al rapporto aureo attraverso la sequenza di Fibonacci che è data da
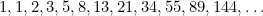 |

Semi di girasole, disposti usando i numeri di Fibonacci |
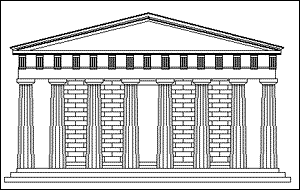
Il Partenone, che incarna il Rapporto Aureo |
In questa sequenza ogni termine è la somma dei due termini precedenti. Fibonacci la scoprì nel XV secolo nel tentativo di prevedere la futura popolazione di conigli. Se si prende il rapporto di ogni termine con quello successivo, si ottiene la sequenza di numeri
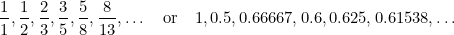 |
e questi numeri si avvicinano sempre più (avete indovinato) al Rapporto Aureo 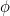 .
.
Trovando entrambe le radici dell’equazione quadratica di cui sopra possiamo effettivamente trovare una formula per l’ennesimo termine della sequenza di Fibonacci. Se  è il
è il 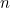 simo numero con
simo numero con 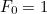 e
e 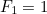 allora
allora  è dato dalla formula
è dato dalla formula
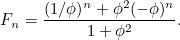 |
Le coniche collegano le equazioni quadratiche alle stelle

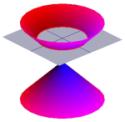
I greci erano anche molto interessati alla forma dei coni. L’immagine a sinistra mostra un tipico cono.
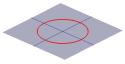
La metà del cono può essere visualizzata come la diffusione della luce proveniente da una torcia. Ora, se fai brillare una torcia su una superficie piatta come un muro, vedrai varie forme mentre muovi la torcia. Queste forme sono chiamate sezioni coniche e sono le curve che si ottengono se si prende una fetta attraverso un cono a vari angoli diversi. Proprio queste curve sono state studiate dai greci, e hanno riconosciuto che ci sono fondamentalmente quattro tipi di sezioni coniche. Se si prende una sezione orizzontale attraverso il cono, si ottiene un cerchio. Una sezione ad un piccolo angolo rispetto all’orizzontale dà un’ellisse. Se si prende una sezione verticale si ottiene un’iperbole e se si prende una sezione parallela a un lato del cono si ottiene una parabola. Queste curve sono illustrate qui sotto.
 |
 |
 |
 |
 |
 |
 |
 |

Una sezionesezione di un cono può essere un cerchio… |

… un’ellisse … |
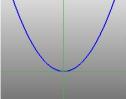
… una parabola … |
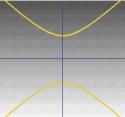
…. o un’iperbole. |
Le sezioni ioniche entrano nella nostra storia perché ciascuna di esse è descritta da un’equazione quadratica. In particolare, se 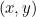 rappresenta un punto su ogni curva, allora un’equazione quadratica collega
rappresenta un punto su ogni curva, allora un’equazione quadratica collega  e
e 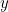 . Abbiamo:
. Abbiamo:
Il cerchio: 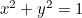 ;
;
L’ellisse: 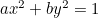 ;
;
L’iperbole: 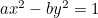 ;
;
La parabola: 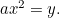
Queste curve erano conosciute e studiate fin dai Greci, ma a parte il cerchio non sembravano avere alcuna applicazione pratica. Tuttavia, come vedremo nel prossimo numero di Plus, un collegamento tra le equazioni quadratiche e le coniche, unito a un potente colpo di fortuna, portò alla comprensione del modo in cui funzionava l’universo, e nel XVI secolo arrivò il momento in cui le coniche cambiarono il mondo.
Chi sono gli autori
Chris Budd è professore di matematica applicata nel dipartimento di scienze matematiche dell’Università di Bath, e la cattedra di matematica alla Royal Institution di Londra.
Chris Sangwin fa parte dello staff della Scuola di matematica e statistica dell’Università di Birmingham. È un Research Fellow nel centro Learning and Teaching Support Network per la matematica, la statistica e la ricerca operativa.
Hanno scritto di recente il popolare libro di matematica Mathematics Galore!, pubblicato dalla Oxford University Press.
Questo articolo è stato ispirato in parte da un notevole dibattito nella Camera dei Comuni britannica sul tema delle equazioni quadratiche. La registrazione di questo dibattito può essere trovata in Hansard, United Kingdom House of Commons, 26 giugno 2003, Colonne 1259-1269, 2003, che è disponibile online sul sito web House of Commons Hansard Debate.