A negyedik osztályos Alice azt kérdezi: “Hány átló van a tízszögben?”
Nagyszerű kérdés, Alice. De ahelyett, hogy választ adnék neked erre a kérdésre, megmutatom, hogyan tudod magad kitalálni. És nem csak azt, hanem azt is megmutatom, hogyan tudod kitalálni a választ bármilyen sokszögre, még akkor is, ha annak 20, vagy 50, vagy 2000 oldala van!
Készen állsz? Kezdjük egy egyszerű példával. Vegyünk egy olyan sokszöget, amelynek 8 oldala van (amit nyolcszögnek nevezünk), így:
Most, ennek a sokszögnek, mivel nyolc oldala van, nyolc csúcsa is van. Kicsit túlterhelőnek tűnik, hogy megpróbáljuk kitalálni az összes átlót, ezért koncentráljunk csak egy csúcsra. Hány olyan átlót tudsz megrajzolni egy nyolcszögben, amelyek mind egy csúcsban kezdődnek?
A válasz erre a kérdésre öt. Nézd meg az alábbi ábrát:

Az ábrán a bal oldali átlót választottam, közvetlenül a felső csúcs alatt, és minden olyan csúcsra rajzoltam átlót, amelyre átlót tudok rajzolni. Melyik átlóra nem tudok átlót rajzolni? Nos, nem rajzolhatok átlót egy csúcsból vissza önmagába, és nem rajzolhatok átlót a mellette lévő két csúcsba sem (mert azok nem átlók lennének, hanem oldalak!).
Az adott csúcsból tehát három csúcsba nem rajzolhatok átlót. Összesen nyolc csúcs, mínusz a három, amire nem tudok rajzolni, marad öt. Ezt fontos megjegyezni: vonj le 3-at a csúcsok számából, és megkapod a bármelyik csúcsból rajzolható átlósok számát.
De ez csak egy csúcs! Bármelyik csúcsból rajzolhatsz átlót, nem? Persze! És a nyolcszögünknek nyolc csúcsa van, tehát vesszük az egy csúcsra jutó átlósok számát, és megszorozzuk a csúcsok számával: 5 x 8 = 40.
Kísértésed lehet azt hinni, hogy ez a válaszunk, de ez nem így van. Miért nem? Mert minden átlót kétszer számoltunk meg! Minden átlónak két csúcsa van, tehát megszámoltuk az egyik végéről, és megszámoltuk a másik végéről is. Tehát ahhoz, hogy megkapjuk az átlósok tényleges számát, el kell osztanunk a válaszunkat 2-vel. 40 / 2 = 20. Egy nyolcszögben húsz átló van.
Próbáljuk ki ezt az érvelést egy olyan sokszögre, amelynek 2000 oldala van. Most nem rajzolok nektek egy 2000 oldalú szöget; az érvelést kép nélkül kell kidolgoznunk.
- Válasszunk ki egy csúcsot. Hány átlót tudsz rajzolni ebből a csúcsból? Válasz: 2000 – 3 = 1997.
- Hány csúcsa van összesen? Válasz: 2000
- Hány átlót számoltunk az összes csúcsból? Válasz: Hány csúcspontot számoltak meg? 1997 x 2000 = 3,994,000
- Hoppá! Minden átlót kétszer számoltunk meg! Hogyan szabaduljunk meg a duplikációktól? Válasz: A duplikációkat nem tudjuk eltávolítani: 3994000 / 2 = 1,997,000
Egy 2000-es szögnek tehát 1,997,000 átlója van!
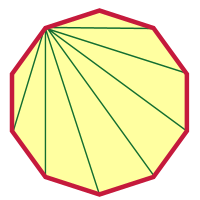
Egy olyan őrültség után, mint a 2000-es szög, egy tízszög már nem is tűnik olyan nehéznek, igaz? Elkezdem, és innen már be is fejezheted. Kiválasztottam egy csúcsot, és abból a csúcsból átlót rajzoltam.
Hány van belőle? Ki tudtad számolni, hogy hány van, anélkül, hogy megnézted volna a képet?
Ki tudod számolni innen? Remélem, hogy igen! Sok szerencsét, Alice!
Apropó, van egy képlet, amit használhatsz; így néz ki: D = n(n – 3)/2. De őszintén szólva nem várom el a diákjaimtól, hogy megjegyezzék. Azt várom el tőlük, hogy emlékezzenek arra, ahogyan ezt itt kiszámoljuk. Ha megértik a logikát, az még jobb, mintha lenne egy képlet!