A szabályozók különböző típusait a szabályozó rendszerek teljesítményének javítására használják. Ebben a fejezetben az olyan alapvető szabályozókat tárgyaljuk, mint az arányos, a derivált és az integrál szabályozók.
Az arányos szabályozó
Az arányos szabályozó olyan kimenetet állít elő, amely arányos a hibajellel.
$$u(t) \propto e(t) $$
$$$\Jobboldali nyíl u(t)=K_P e(t)$$
Alkalmazzuk a Laplace-transzformációt mindkét oldalon –
$$U(s)=K_P E(s)$$
$$$\frac{U(s)}{E(s)}=K_P$$
Ezért, az arányos szabályozó átviteli függvénye $K_P$.
Hol,
U(s) az u(t)
működtető jel Laplace-transzformáltja
E(s) az e(t)
hibajel Laplace-transzformáltja
KP az arányossági állandó
Az egységesen negatív visszacsatolású zárt hurkú szabályozórendszer blokkdiagramja az arányos szabályozóval együtt a következő ábrán látható.
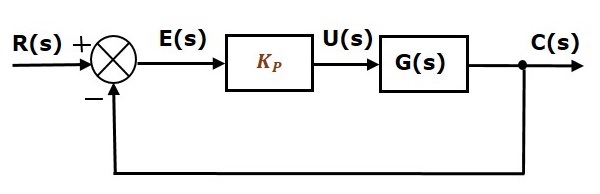
Az arányos szabályozót arra használjuk, hogy a tranziens választ a követelménynek megfelelően megváltoztassuk.
Deriváló szabályozó
A deriváló szabályozó egy kimenetet állít elő, amely a hibajel deriváltja.
$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}t}$$
Alkalmazzuk a Laplace transzformációt mindkét oldalon.
$$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$$
Ezért a derivált szabályozó átviteli függvénye $K_D s$.
Ahol $K_D$ a derivált állandó.
Az egységesen negatív visszacsatolású zárt hurkú szabályozórendszer blokkdiagramja a derivált szabályozóval együtt a következő ábrán látható.
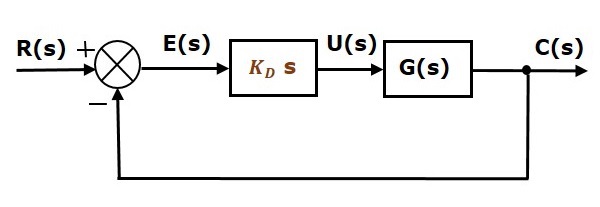
A deriváló szabályozót arra használjuk, hogy az instabil szabályozási rendszert stabillá tegyük.
Integrál szabályozó
Az integrál szabályozó olyan kimenetet állít elő, amely a hibajel integrálja.
$$u(t)=K_I \int e(t) dt$$
Alkalmazzuk a Laplace-transzformációt mindkét oldalon –
$$U(s)=\frac{K_I E(s)}{s}$$
$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$$
Ezért, az integrál szabályozó átviteli függvénye $\frac{K_I}{s}$.
Ahol $K_I$ az integrálkonstans.
Az egységesen negatív visszacsatolású zárt hurkú szabályozórendszer blokkdiagramja az integrál szabályozóval együtt a következő ábrán látható.
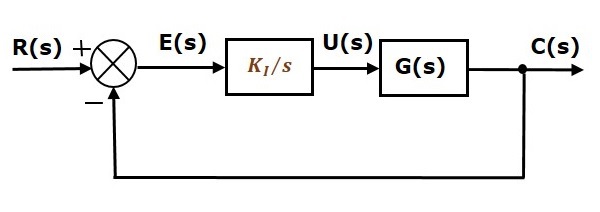
Az integrál szabályozót az állandósult állapot hibájának csökkentésére használjuk.
Az alapszabályozók kombinációját tárgyaljuk most.
Proporcionális derivált (PD) szabályozó
A proporcionális derivált szabályozó egy kimenetet állít elő, amely az arányos és a derivált szabályozó kimeneteinek kombinációja.
$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}t}$$
Alkalmazzuk a Laplace transzformációt mindkét oldalon – –
$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$$
Ezért, az arányos derivált szabályozó átviteli függvénye $K_P + K_D s$.
Az egységesen negatív visszacsatolású zárt hurkú szabályozórendszer blokkdiagramja az arányos derivált szabályozóval együtt a következő ábrán látható.
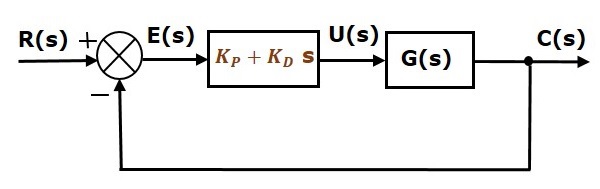
Az arányos derivált szabályozót a szabályozási rendszer stabilitásának javítására használják anélkül, hogy az állandósult állapot hibáját befolyásolná.
Proporcionális integrál (PI) szabályozó
Az arányos integrál szabályozó egy kimenetet állít elő, amely az arányos és az integrál szabályozó kimeneteinek kombinációja.
$$u(t)=K_P e(t)+K_I \int e(t) dt$$
Alkalmazzuk a Laplace transzformációt mindkét oldalon –
$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$$
Ezért, az arányos integrál szabályozó átviteli függvénye $K_P + \frac{K_I} {s}$.
Az egységesen negatív visszacsatolású zárt hurkú szabályozórendszer blokkdiagramja az arányos integrál szabályozóval együtt a következő ábrán látható.
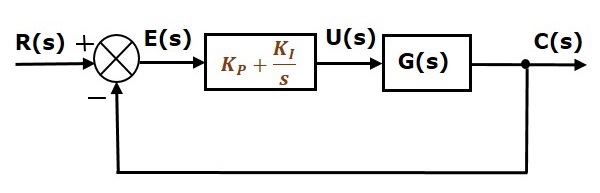
Az arányos integrál szabályozót az állandósult állapot hibájának csökkentésére használjuk anélkül, hogy befolyásolná a szabályozórendszer stabilitását.
Proporcionális integrál derivált (PID) szabályozó
A arányos integrál derivált szabályozó egy kimenetet állít elő, amely az arányos, integrál és derivált szabályozó kimeneteinek kombinációja.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$
Alkalmazza a Laplace-transzformációt mindkét oldalon –
$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$$
Ezért, az arányos integrál-derivált szabályozó átviteli függvénye $K_P + \frac{K_I} {s} + K_D s$.
Az egységesen negatív visszacsatolású zárt hurkú szabályozórendszer blokkdiagramja az arányos integrál derivált szabályozóval együtt a következő ábrán látható.
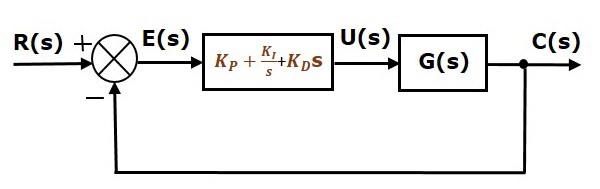
Az arányos integrál derivált szabályozót a szabályozórendszer stabilitásának javítására és az állandósult állapot hibájának csökkentésére használjuk.