A szög, amelyet akkor zárunk be, ha a sugarat
körbe tekerjük:
 |
1 radián körülbelül 57,2958 fok. |
Miért “57,2958…” fok? Mindjárt meglátjuk.
A radián egy tiszta mértékegység, amely a kör sugarán alapul:
Radián: az a szög, amely akkor keletkezik, ha fogjuk a sugarat
és körbetekerjük a kört.
Radiánok és fokok
Lássuk, miért egyenlő 1 radián 57.2958… fok:
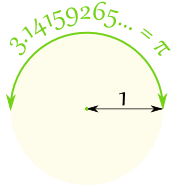
Egy félkörbenπ sugár van, ami szintén 180°
Hogy radiánból fokba menjünk: szorozzuk 180-al, osszuk π-vel
Hogy fokból radiánba menjünk: szorozzuk π-vel, osszuk 180-al
Itt van egy táblázat az egyenértékű értékekről:
| fok | Radiánok (pontos) |
Radiánok (kb) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0.785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1.571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4.712 |
| 360° | 2π | 6.283 |
Példa: Hány sugár van egy teljes körben?
Elképzeljük, hogy egy kör középpontjától a kerületéig pontosan olyan hosszúságú zsinórdarabokat vágunk …
… hány darabra van szükséged ahhoz, hogy egyszer körbejárd a kört?
Válasz: 2π (vagy kb. 6,283 darab madzag).
A matematikusok által kedvelt radiánok
Mivel a radián azon a tiszta elképzelésen alapul, hogy “a sugarat a kerület mentén fektetjük”, gyakran ad egyszerű és természetes eredményeket, amikor a matematikában használjuk.
Nézzük például a szinuszfüggvényt nagyon kis értékekre:

