Az egyik fontos kérdés az, hogy hogyan oszlanak el a prímszámok az egész számok között? A válasz nagyon röviden: meglehetősen véletlenszerűen, bizonyos alapstatisztikák ismeretében…
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Kanada
Email Bill Casselman
| |
|
Bevezetés
Néhány évvel ezelőtt feltételezték, hogy végtelen sok olyan $p$, $q$ prímszámpár létezik, ahol $q = p+2$. A közelmúltban történt némi (és híres) előrelépés ebben a problémában. Keveset fogok szólni a legújabb eredményekről, ehelyett inkább arról beszélek, hogy mit várunk – és nem arról, hogy mit tudunk – az ilyen párokról. Semmi újat nem fogok mondani, és bizonyos mértékig csak azt dolgoztam ki, amit Andrew Granville mond a közelmúltbeli előrelépésekről szóló ismertető jegyzetében.
Hány prímszámra számíthatunk?
A prímszám olyan pozitív egész szám, amelynek nincs osztója önmagán és $1$-on kívül. A definíció egyszerű, de amint elkezdjük feltárni a prímszámok jelentőségét, rájövünk, hogy sok finom viselkedést mutatnak. Az egyik fontos kérdés, hogy hogyan oszlanak meg a prímszámok az egész számok között? A válasz nagyon röviden: meglehetősen véletlenszerűen, bizonyos alapstatisztikák mellett. Mit értek ez alatt?
Nos, íme egy négyzetes tömb, amely az összes prímszámot ábrázolja $400$-ig:

Ebben a tömbben van néhány minta, amelyek közül néhányat később kommentálni fogok. A legtöbbet, amit érzékelsz, a kijelző valamilyen artefaktuma okozza. Például minden második oszlop lényegében üres, és ez azért van, mert az egyetlen páros prímszám a $2$. Továbbá minden ötödik oszlop lényegében üres. Érdekesebbek az ikerprím párok (amelyek közül néhány nem annyira látható, mert két sorra oszlik, például $59$, $61$), valamint néhány, az utolsó megjelenített számjegyekkel kapcsolatos minta. Ezeket nevezhetjük helyi mintázatoknak. Globálisak nem látszanak.
Nagy erőfeszítéseket tettek a prímszámok előállításának rendkívül hatékony módjaira, de manapság még egy nagyon egyszerű programnak is csak kis időbe telik nagy prímszámlistákat készíteni. Az egyik legeredményesebb program elkészít egy nagy prímszámlistát, majd ezt felhasználva kiszámítja a $\pi(n)$ függvényt, a $\le n$ prímszámok számát.
Egy dolog, amire ez használható, az az, hogy nagyjából képet kapjunk a prímszámok gyakoriságáról. A $$:
tartományban $135$ prímszám van:

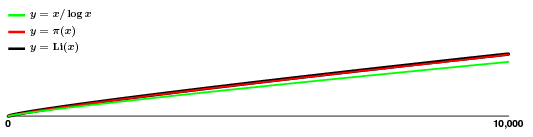
A közelítés jól néz ki! Tehát, még ha $\pi(x)$ egy kicsit ugrál is, látszólag különösebb minta nélkül, elég jó becslésünk van rá, ami azt jelenti, hogy jó képünk van a prímszámok növekedéséről, legalábbis átlagosan.
Nem szabad azonban elfelejteni, hogy a látszólagos simaság csalóka. Közelről nézve így néz ki a két felső görbe:

Kommentárok?
Heurisztikus következtetés az ikerprímekről
Az ikerprímek olyan $p$, $p+2$ pár, amelyek mindketten prímek. Például a fenti ábrák egyikéből láthatjuk az ikerprímeket $$ , , , , , , , , , $$$
és másokat. Feltételezték, hogy végtelen sok van belőlük, de bár erre sok empirikus bizonyíték van, még nem sikerült bizonyítani.
A legerősebb bizonyíték talán egy képlet, amely figyelemre méltóan jól közelíti az ikerprímek $\pi_{2}(x)$ számát $\le x$. Nem vagyok egészen biztos ennek a képletnek az eredetét illetően, de először G. H. Hardy és J. E. Littlewood (maguk is egy ikerprímszám-pár) 1923-ban kelt tanulmányában jelent meg. A dolgozat több hasonló formulát tartalmaz, amelyek mind ugyanarra a módszerre épülnek, amellyel már korábban is számos probléma megoldására használták. Ez volt az ő kör módszerük. A $\pi_{2}(x)$-ra vonatkozó képletük levezetése egyáltalán nem szigorú, de nagyon meggyőző. Andrew Granville cikkének függelékében van erről egy tömör beszámoló.
De közvetlenül a második világháború után Lord Cherwell (Frederick Lindemann) egy elemi valószínűségi (és még mindig nem meggyőző) levezetést javasolt. Ez E. M. Wrighttal való együttműködéshez és végül egy posztumusz közös publikációhoz vezetett. Ezt Hardy és Wright jól ismert szövegének 22.20. szakasza fejti ki. Ennek egy kissé elemi változata Granville cikkének egyik függelékében is megtalálható (2.5. szakasz). Követem őt.
A plauzibilis érvelés kiindulópontja a $\pi(x)$-ra, az $x$-nél kisebb vagy azzal egyenlő prímszámok számára adott becslésünk. A levezetés alapgondolata az, hogy a prímszámok jórészt véletlenszerűen oszlanak el. Tudjuk, hogy $x$ környékén a prímszámok sűrűsége körülbelül $1/\log x$. Ha a prímszámok véletlenszerűen oszlanának el, akkor annak valószínűsége, hogy két adott szám $x$ közelében prímszám, csak a helyi valószínűségek szorzata lenne, ami $1/\log^{2} x$. Ez minden bizonnyal csalóka érvelés, hiszen ha $n > 2$, akkor annak a valószínűsége, hogy mind $n$, mind $n+1$ prímszám, $0$, míg az a tény, hogy $p$ prímszám, úgy tűnik, növeli annak az esélyét, hogy $p+2$ is az. Hasonló megfontolásokat kell figyelembe venni a $x$ szomszédságában lévő más kis prímszámokkal való esetleges oszthatóság miatt is.
Ezzel a történettel kapcsolatban van egy egyszerű tény. Ha $q$ egy tetszőleges prímszám, akkor annak valószínűsége, hogy véletlenszerűen olyan egész számot választunk, amely nem osztható $q$-val, $1-1/q$. Két olyan szám kiválasztásának valószínűsége, amelyek nem oszthatók $q$-val, tehát a $(1 – 1/q)^{2}$ szorzata. Tegyük fel, hogy $p$ és $p+2$ is prímszám, akkor sem $p$, sem $p+2$ nem osztható $q$-val. Ha $q = 2$, akkor ez $1/2$-szer fordul elő. Ha $q \ne 2$, akkor annak a valószínűsége, hogy $p \nem \equiv 0$ és $p \nem \equiv -2$ modulo $q$, $(1 – 2/q)$. A kínai maradéktétel miatt a két prímszámmal való oszthatóság független esemény. Ha tehát $x$ nagy és $Q$ viszonylag kicsi, akkor annak valószínűsége, hogy $x$ közelében lévő $m$ és $n$ számpár $Q$-ig nem lesz bármely prímszám többszöröse, $$$ { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Legyen $\Gamma_{Q}$ ennek és $\prod_{q \le Q}(1 – 2/q)$ hányadosa: $$$ \Gamma_{Q} = { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ Megvan $$ { { 1 – 2/q \over (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Egy standard kritérium azt állítja, hogy ez a szorzat konvergál, ha az $\összeg 1/(q-1)^{2}$ konvergál. De konvergál, mivel az integrálpróba azt mondja, hogy $\sum 1/n^{2}$ konvergál. Ezért ez a szorzat valójában egy $\Pi_{\infty}$ számhoz konvergál, ahogy $Q \rightarrow \infty$. Legyen $C_{2}$ az inverze. Granville cikkének 2.5. szakasza szerint ezen a ponton intuitíve ésszerűnek kell lennie, hogy a $\pi_{2}(x)$ iker prímszámok $\le x$ számát az $$ \Pi_{2}(x) = C_{2}$ közelíti. \int_{2}^{\infty} { dx \over \log^{2} x } \, . $$
Hardy és Wright szövege egy alaposabb elemzést tartalmaz, amely az intuitív ugrást egy kicsit világosabbá teszi.
A konstans értékét itt J. W. Wrench már régen kiszámította, hogy körülbelül $1.3203236316937391414785562422002911155686525 \ldots $. Íme a $\pi_{2}(x)$ néhány értékének és a képletnek az összehasonlítása a $$ tartományban: $$$ \matrix{ n & 10,000 & 20,000 & 30,000 & 40,000 & 50,000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } \cr } $$ $$ \matrix{ n & 60,000 & 70,000 & 80,000 & 90,000 & 100,000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \fantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Kommentárok?
Dickson sejtése
A kettős prímek egy sokkal általánosabb dolog speciális esete. Megkérdezhetjük, hogy vannak-e végtelen sok olyan $p$, $p+4$ vagy $p$, $p+6$ párok, amelyek prímek? Vagy $p$, $p+10$? A $p$ és $p+10$ esetét mindenképpen sugallja az egyik fenti kép, amelyen jól láthatóak az ilyen párok. Mi a helyzet valamilyen hármasokkal? Tegyük fel, hogy $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ alkotnak egy egész számokból álló tömböt. Várható-e, hogy végtelen sok olyan $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ halmaz létezik, amelyek mindegyike prím?
Egy kicsit óvatosnak kell lenni. Nincsenek $p$, $p+1$ alakú prímszámpárok (elmúlt $p = 2$), mert e két szám közül az egyiknek osztandónak kell lennie $2$-val. Hasonlóképpen, $p = 3$ után nincsenek $p$, $p+2$, $p+4$ prímhármasok, mert ezek közül az egyiknek oszthatónak kell lennie $3$-mal.
Ez utóbbi példa tanulságos lehet. A $p+4$ szám akkor és csak akkor osztható $3$-al, ha $p+1$ is osztható $3$-al. Tehát $3$ akkor és csak akkor osztja az $p$, $p+2$, $p+4$ számok valamelyikét, ha osztja az $p$, $p+1$, $p+2$ számokat. De ez biztos, hiszen az utolsó hármas egyértelműen lefedi az összes modulo $3$ számot.
Általában $p$ akkor mondható a $(a_{i})$ tömb akadályának, ha $p$ mindig minden $n+a_{i}$ sorozatból ($i = 1$, $\ldots$, $k$) legalább egyet oszt. Ez akkor és csak akkor történik meg, ha a számok $a_{i} \; {\rm mod} \, p$ kitöltik az egész $Z/p$-t.
Ez soha nem történhet meg, ha $p > k$, tehát annak ellenőrzéséhez, hogy valamely $p$ akadályozza-e a $(a_{i})$-t, csak azt kell ellenőriznünk, hogy az $a_{i}$ minden $p \le k$ esetén lefedi-e a $Z/p$ -t. A $(a_{i})$ tömböt elfogadhatónak nevezzük, ha nincs prímszámú akadálya.
A $(1,3,7,9)$ például elfogadható tömb, hiszen, mint könnyen ellenőrizhetjük, sem $2$, sem $3$ nem akadály. A fenti ábrák egyikén több, ebbe a mintába illeszkedő prímsorozat is látható. További példák: (a) tetszőleges $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Léteznek tetszőlegesen nagy megengedhető halmazok. Valójában:
Tétel. Ha $a_{1}$-től $a_{k}$-ig $> k$ különböző prímszámok tetszőleges halmaza, akkor ezek egy megengedhető halmazt alkotnak.
Miért van ez így? Ha $p$ bármely prím, ahol $p> k$, akkor már láttuk, hogy nem lehet akadály. De ha $p \le k$, akkor nem oszthat meg egyetlen $a_{i}$-t sem, amelyek közül egyik sem lehet kongruens $0$ modulo $p$-val. Tehát az $a_{i}$ nem tölti ki a $Z/p$-t.
Az eredetileg L. E. Dickson által megfogalmazott sejtés egy speciális esete, hogy ha $(a_{i})$-nak nincs prím akadálya, akkor létezik végtelen számú $(n +a_{i})$ alakú prímsorozat.
Az utóbbi időben történtek
Ez nem a megfelelő hely a teljes történet elmesélésére, amelyről más helyeken már alaposan beszámoltunk. Különösen ajánlom Erica Klarreich Quanta-cikkét egy népszerű beszámolóhoz, és Granville esszéjét egy technikásabb beszámolóhoz. Csak azt szeretném egy kicsit pontosabban megfogalmazni, mint Klarreich beszámolójában, hogy mi a leghíresebb új eredmény.
Ez Yitang Zhangnak köszönhető. A legegyszerűbb állítása annak, amit ő bizonyított, hogy létezik végtelen sok olyan $[n, n+70 000 000)$ intervallum, amely legalább két prímszámot tartalmaz. Ez gyengébb, mint az ikerprímek sejtése, de fogalmilag nagyon közel áll hozzá. A későbbi munkákban (sok matematikus által) a rés nagyságát erősen csökkentették, de feltehetően a jelenlegi módszerekkel nem lehet $2$-ra csökkenteni.
A Granville által kifejtettek szerint Zhang első és vitathatatlanul fő eredménye az, hogy létezik $k$ olyan tulajdonsággal, hogy ha $a_{1}$, $\ldots$ , $a_{k}$ egy $k$ elemű megengedhető halmaz, akkor létezik végtelen számú $n$ olyan, hogy $\{ n +a_{i} \}$ legalább két prímszámot tartalmaz. (Klarreich Quanta cikkében a tömböt “fésűnek” nevezi. Ne feledjük, hogy Dickson sejtése szerint azt várnánk, hogy minden $k$ prímszám). Valójában Zhang bebizonyította, hogy ez az állítás igaz egy bizonyos $k =3,500,000$, amely egy $70,000,000$-os intervallumot ölel fel. A mára már híres következmény az, hogy bizonyos $m \lt 70 000 000$ esetén létezik végtelen számú $p$, $p+m$ prímpár.
Tovább olvasva
- Lord Cherwell és E. M. Wright, “The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Aki tud valamit Lord Cherwell, más néven Frederick Lindemann életéről, az nagyon meglepődik, ha megtudja, hogy milyen mértékben járult hozzá a számelmélethez. A Wikipédia életrajza nem utal kellőképpen a második világháború alatt Churchill legfőbb tudományos tanácsadójaként szerzett rossz hírnevének minden okára.
- L. E. Dickson, “A new extension of Dirichlet’s theorem on prime numbers”, Messenger of Mathematics 33.
Lásd a Wikipédia bejegyzését is Dickson sejtéséről.
- Andrew Granville, “Prímszámok korlátos hosszúságú intervallumokban”. Elérhető a honlapjáról.
- G. H. Hardy, Ramanujan, Cambridge University Press.
A 2.5. szakasz tartalmazza a $\pi(x)$ egy lehetséges képletének ideális levezetését.
- G. H. Hardy és J. E. Littlewood, “Some problems of ‘Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy és E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, “Together and alone, closing the prime gap”, Quanta November 19, 2013.
- B. Riemann, “Egy adott mennyiségnél kisebb prímszámok számáról”. Ennek a klasszikusnak David Wilkins által készített angol fordítása elérhető a Wikipédia egyik linkjéről.
Ez többek között felvázolja a $\pi(x)$ közelítő képletének levezetését.
- J. W. Wrench, “Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
A $C_{2}$ egy korai számítása.
- Prímszámok listái $1,000,000,000,000,000,000$-ig
- Az első 20,000 ikerprímszám listája.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman
.