Matematikai modellezés

by admin Leave Comment

Tanulmányi célok

  • Elvezetés a darabonkénti függvényekbe
    • Definiáljuk a darabonkénti függvényeket. függvény
    • Egy darabos függvény kiértékelése
    • Egy darabos függvény megírása adott alkalmazás esetén
  • Grafikus darabos függvények
    • Adott egy darabos-definiált függvényt, vázolj fel egy gráfot
    • Írd fel egy darabos függvény tartományát és tartományát adott gráf

Néhány függvény darabos. Ebben a részben azt fogjuk megtanulni, hogyan definiálhatunk és gráfolhatunk olyan függvényeket, amelyek lényegében diszkrét darabok gyűjteményei. Az így definiált dolgok közé tartozik például egy autó profiljának megtervezése, a mobiltelefon-csomag kiszámítása és a jövedelemadó-kulcsok kiszámítása. Az adókulcsod például a jövedelmedtől függ, és egy jövedelemtartomány esetén azonos, ahogyan azt az alábbi táblázat mutatja:

Marginális adókulcs Szingli adóköteles jövedelem Házaspár vagy minősített özvegy(ek) adóköteles jövedelme. Adóköteles jövedelem Külön adózó házasok Adóköteles jövedelem Háztartásfő adóköteles jövedelme
10% $0 – $9,275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% $415,051+ $466,951+ $233,476+ $441,001+

A darabonkénti függvény olyan függvény, amelyben egynél több képletet használnak a tartomány különböző darabjain a kimenet meghatározására.

A darabonkénti függvényeket olyan helyzetek leírására használjuk, amelyekben egy szabály vagy kapcsolat megváltozik, amint a bemeneti érték átlép bizonyos “határokat”. Például az üzleti életben gyakran találkozunk olyan helyzetekkel, amelyekben egy bizonyos tétel darabonkénti költsége levonásra kerül, amint a megrendelt darabszám meghalad egy bizonyos értéket. Az adózási zárójelek a darabonkénti függvények másik valós példája. Vegyünk például egy egyszerű adórendszert, amelyben a 10 000 dollárig terjedő jövedelmek 10%-kal adóznak, és minden további jövedelem 20%-kal adózik. A teljes jövedelemre, S-re kivetett adó 0,1S lenne, ha S\le 10 000 dollár, és 1000 + 0,2 (S – 10 000 dollár), ha S> 10 000 dollár.

darabonkénti függvény

A darabonkénti függvény olyan függvény, amelyben egynél több képletet használnak a kimenet meghatározásához. Minden egyes képletnek saját tartománya van, és a függvény tartománya ezeknek a kisebb tartományoknak az uniója. Ezt az elképzelést így jegyezzük le:

f\left(x\right)=\begin{esetek}\text{1. formula, ha x az 1. tartományban van}\\\ \text{2. formula, ha x a 2. tartományban van}\\\ \text{3. formula, ha x a 3. tartományban van}\end{esetek}

A darabosan meghatározott függvény abszolút értékű jelölése

|x|=\begin{cases}x\text{ if }x\ge 0\\\\ -x\text{ if }x<0\end{cases}

Darabosan meghatározott függvény kiértékelése

Az első példában megmutatjuk, hogyan kell kiértékelni egy darabosan meghatározott függvényt. Vegyük észre, hogy fontos figyelni a tartományra annak meghatározásához, hogy milyen kifejezéssel értékeljük ki a bemenetet.

Példa

Adott a függvény

f(x)=\begin{cases}7x+3\text{ if }x<0\\\7x+6\text{ if }x\ge{0}\end{cases},

értékeljük:

  1. f (-1)
  2. f (0)
  3. f (2)
Show Answer

1.Az f(x) definíciója 7x+3, ha x=-1\text{ mert }-1<0.

Értelmezzük: f(-1)=7(-1)+3=-7+3=-4

2. Az f(x) definíciója 7x+6, ha x=0\text{ mert }0\ge{0}.

Értékeljük: f(0)=7(0)+6=0+6=6

3. Az f(x) definíciója 7x+6, ha x=2\text{ mert }2\ge{0}.

Értékeljük ki: f(2)=7(2)+6=14+6=20

A következő videóban megmutatjuk, hogyan lehet több értéket kiértékelni egy darabonként meghatározott függvényt.

A következő példában megmutatjuk, hogyan kell kiértékelni egy olyan függvényt, amely egy telefontársaság adatátviteli költségét modellezi.

Példa

Egy mobiltelefontársaság az alábbi függvényt használja arra, hogy meghatározza a g gigabájtnyi adatátvitel költségét, C-t, dollárban kifejezve.

C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Következtesse a költséget, ha 1.5 gigabájtnyi adat felhasználásának költségét és a 4 gigabájtnyi adat felhasználásának költségét.

Válasz megjelenítése

Az 1,5 gigabájtnyi adat felhasználásának költségét, C(1,5), először megnézzük, hogy a bemenetünk a tartomány melyik részére esik. Mivel az 1,5 kisebb, mint 2, az első képletet használjuk.

C(1,5) = 25 $

A 4 gigabájtnyi adat felhasználásának költségét, C(4), megkeresve látjuk, hogy a 4-es bemenetünk nagyobb, mint 2, így a második képletet használjuk.

C(4)=10(4)+5=45

A megoldás elemzése

A függvényt az alábbi grafikonon ábrázoljuk. Láthatjuk, hogy hol változik a függvény konstansból pozitív meredekségű egyenesre g=2-nél. A különböző képletek grafikonjait közös tengelyeken ábrázoljuk, ügyelve arra, hogy minden képletet a megfelelő tartományon alkalmazzunk.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Darabonként definiált függvény írása

Az utolsó példában megmutatjuk, hogyan írjunk egy darabonként definiált függvényt, amely egy múzeumi tárlatvezetés árát modellezi.

Példa

Egy múzeum 1-9 fős csoport esetén személyenként 5 dollárt kér a tárlatvezetésért, 10 vagy több fős csoport esetén pedig fix 50 dollárt. Írjunk függvényt, amely a személyek számát, n, és a költséget, C, összekapcsolja.

Válasz megjelenítése

Két különböző képletre lesz szükség. A 10 alatti n-értékek esetén C=5n. 10 vagy nagyobb n értékek esetén C=50.

C(n)=\begin{cases}{5n}\text{ if }{0}<{n}<{10}\\ 50\text{ if }{n}\ge 10\end{cases}

A megoldás elemzése

A függvényt a 21. ábra mutatja. A grafikon egy átlós egyenes n=0-tól n=10-ig, utána pedig egy konstans. Ebben a példában a két képlet megegyezik a találkozási pontban, ahol n=10, de nem minden darabos függvény rendelkezik ezzel a tulajdonsággal.

A következő videóban egy példát mutatunk egy darabosan meghatározott függvény felírására egy forgatókönyv alapján.

Adott egy darabos függvény, írja fel a képletet, és határozza meg a tartományt minden intervallumhoz.

  1. Identifikálja azokat az intervallumokat, amelyekre különböző szabályok vonatkoznak.
  2. Meghatározza azokat a képleteket, amelyek leírják, hogyan kell kiszámítani egy kimenetet egy bemenetből az egyes intervallumokban.
  3. A függvény megírásához használjon zárójeleket és if-állításokat.

Darabonkénti függvények ábrázolása

Ebben a részben darabonkénti függvényeket fogunk ábrázolni. Az alább ábrázolt függvény egy adott mobiltelefon-társaság adatátviteli költségét ábrázolja. Láthatjuk, hogy hol változik a függvény konstansból pozitív meredekségű egyenesre g=2-nél. Amikor darabonkénti függvényeket ábrázolunk, fontos, hogy minden képletet a megfelelő tartományra alkalmazzunk.C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Ebben az esetben a kimenet 25 bármely 0 és 2 közötti bemenet esetén. A 2-vel egyenlő vagy annál nagyobb értékek esetén a kimenet 10g+5.

Adott egy darabonkénti függvény, rajzoljon egy grafikont.

  1. Jelölje meg az x-tengelyen a tartomány minden egyes darabján az intervallumok által meghatározott határokat.
  2. A tartomány minden egyes darabjára grafikonozza az adott intervallumot az adott darabhoz tartozó megfelelő egyenlet segítségével. Ne ábrázoljon két függvényt egy intervallumon, mert az sértené a függvény kritériumát.

Példa

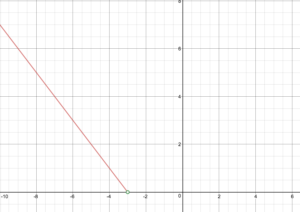
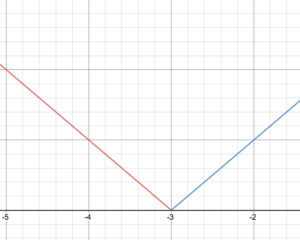
Vázolja fel a függvény grafikonját.

A darabonkénti definíció f(x)=\begin{cases}-x – 3\text{ if }x < -3\\\ x + 3\text{ if} x \ge -3\end{esetek}
Rajzolja meg f grafikonját.
Adja meg a függvény tartományát és tartományát.

Válasz megjelenítése

Először is rajzolja meg az f(x) = -x-3 egyenest, kitörölve azt a részt, ahol x nagyobb -3-nál. Helyezzünk egy nyitott kört a (-3,0) pontba.

Ezután helyezzük el a grafikonon az f(x) = x+3 egyenest a (-3,0) pontból kiindulva. Vegyük észre, hogy a grafikon ezen részén a (-3,0) pont szerepel, így a nyitott kört eltávolíthatjuk.

A két grafikon a (-3,0)

A függvény tartománya az összes valós szám, mert (-3,0)nem szerepel az f(x) = -x-3 végpontjaként, de az f(x) = x+3 végpontjaként szerepel.

Ez a függvény tartománya f(x)=0-nál kezdődik, 0-t is magában foglalja, és a végtelenig tart, tehát ezt így írnánk: x\ge0

A következő példában egy darabonként meghatározott függvényt fogunk ábrázolni, amely egy online képregény-kereskedő szállítási költségét modellezi.

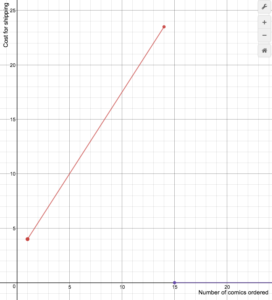
Példa

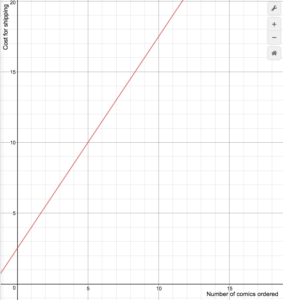
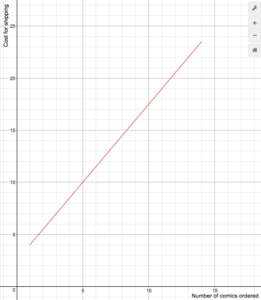
Egy online képregény-kiskereskedő a szállítási költséget a következő képlet szerint számolja fel

S(n)=\begin{cases}1,5n+2.5\text{ ha}1\le{n}\le14\\\0\text{ ha}n\ge15\end{esetek}

Rajzolja fel a költségfüggvény grafikonját.

Válasz megjelenítése

Először is rajzolja fel az S(n)=1,5n+2,5 egyenest. Használhatunk transzformációkat: ez az azonosság 1,5-szeres függőleges megnyújtása és 2,5szeres függőleges eltolása.

S(n)=1,5n+2.5

Most a gráf azon részeit, amelyek nem a tartományban vannak, az 1\le{n}\le14

S(n) = 1,5n+2,5 az 1<=n<=14

Végül adjuk hozzá az S(n)=0 konstans függvényt a 15-nél nagyobb vagy azzal egyenlő bemenetekhez. Helyezzünk zárt pontokat a grafikon végeire, hogy jelezzük a végpontok felvételét.

A következő videóban megmutatjuk, hogyan kell egy darabosan meghatározott függvényt grafikusan ábrázolni, amely mindkét tartományon lineáris.

Összefoglaló

  • A darabos függvény olyan függvény, amelyben egynél több képletet használunk a kimenet meghatározására a tartomány különböző darabjain.
  • A darabos függvény kiértékelése azt jelenti, hogy nagy figyelmet kell fordítanunk arra, hogy az adott bemenetre milyen helyes kifejezést használunk

A darabos függvények grafikus ábrázolásához először meg kell határoznunk, hogy a tartomány hol van felosztva. Grafikusan ábrázolja a függvényeket a tartományon olyan eszközökkel, mint a pontok ábrázolása vagy a transzformációk. Ügyeljünk arra, hogy az egyes tartományok végpontjain nyitott vagy zárt köröket használjunk aszerint, hogy a végpont szerepel-e a tartományban

.

Vélemény, hozzászólás?

Az e-mail-címet nem tesszük közzé.