Előfeltétel – Távolságmérések az adatbányászatban
Az adatbányászatban a hasonlósági mérték az adatobjektum jellemzőit reprezentáló dimenziókkal való távolságot jelenti egy adathalmazban. Ha ez a távolság kisebb, akkor nagyfokú a hasonlóság, ha viszont nagy a távolság, akkor alacsony a hasonlóság mértéke.
A népszerű hasonlósági mértékek közül néhány: –
- Euklideszi távolság.
- Manhattan távolság.
- Jaccard hasonlóság.
- Minkowski távolság.
- Kozinus hasonlóság.
A kozinus hasonlóság egy olyan metrika, amely segít meghatározni, hogy az adatobjektumok méretüktől függetlenül mennyire hasonlóak. Két mondat hasonlóságát mérhetjük Pythonban a Cosine Similarity segítségével. A koszinusz hasonlóságban az adatobjektumokat egy adathalmazban vektorként kezeljük. A képlet két vektor közötti koszinusz hasonlóság meghatározására a következő: –
Cos(x, y) = x . y / ||x|| * ||y||
ahol,
- x . y = az ‘x’ és ‘y’ vektorok szorzata (pont).
- ||x|| és ||y||| = az ‘x’ és ‘y’ vektorok hossza.
- ||x|| * ||y||| = az ‘x’ és ‘y’ vektorok szorzata.
Példa :
Nézzünk egy példát két vektor – ‘x’ és ‘y’ – hasonlóságának meghatározására a koszinusz hasonlóság segítségével.
Az ‘x’ vektor értékei, x = { 3, 2, 0, 5 }
A ‘y’ vektor értékei, y = { 1, 0, 0, 0, 0 }
A koszinusz hasonlóság kiszámításának képlete : Cos(x, y) = x . y / ||x|| * ||y||
x . y = 3*1 + 2*0 + 0*0 + 5*0 = 3||x|| = √ (3)^2 + (2)^2 + (0)^2 + (5)^2 = 6.16||y|| = √ (1)^2 + (0)^2 + (0)^2 + (0)^2 = 1∴ Cos(x, y) = 3 / (6.16 * 1) = 0.49
A két ‘x’ és ‘y’ vektor közötti hasonlóságot –
∴ Dis(x, y) = 1 - Cos(x, y) = 1 - 0.49 = 0.51
- A két vektor közötti koszinusz hasonlóságot ‘θ’-ben mérjük.
- Ha θ = 0°, akkor az ‘x’ és ‘y’ vektorok átfedik egymást, így bizonyítva, hogy hasonlóak.
- Ha θ = 90°, akkor az ‘x’ és ‘y’ vektorok nem hasonlóak.
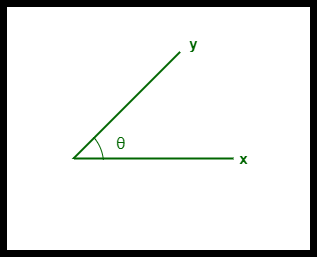
Kozinusz hasonlóság két vektor között
Előnyei :
- A kozinusz hasonlóság azért előnyös, mert még ha a két hasonló adatobjektum az euklideszi távolság szerint messze is van egymástól a méret miatt, akkor is lehet köztük kisebb szög. Minél kisebb a szög, annál nagyobb a hasonlóság.
- A többdimenziós térben ábrázolva a koszinusz hasonlóság az adatobjektumok orientációját (szögét) és nem a nagyságát ragadja meg.