- Hogyan kell használni a Fokozatokból radiánokká alakítót
- Mi a fok?
- A kör fokai
- Mi a radián?
- Kör kerülete
- Sugarak a körben
- Hogyan lehet fokokat radiánokká alakítani
- Fokokból radiánokká tizedes
- A fokok sugárrá alakítása a pí törtrészeként
- Példa: 36 fok átváltása radiánokká
- Hogyan lehet radiánokat fokokká alakítani
- Radiánok fokokká
- Degrees to Radians Updates
Hogyan kell használni a Fokozatokból radiánokká alakítót
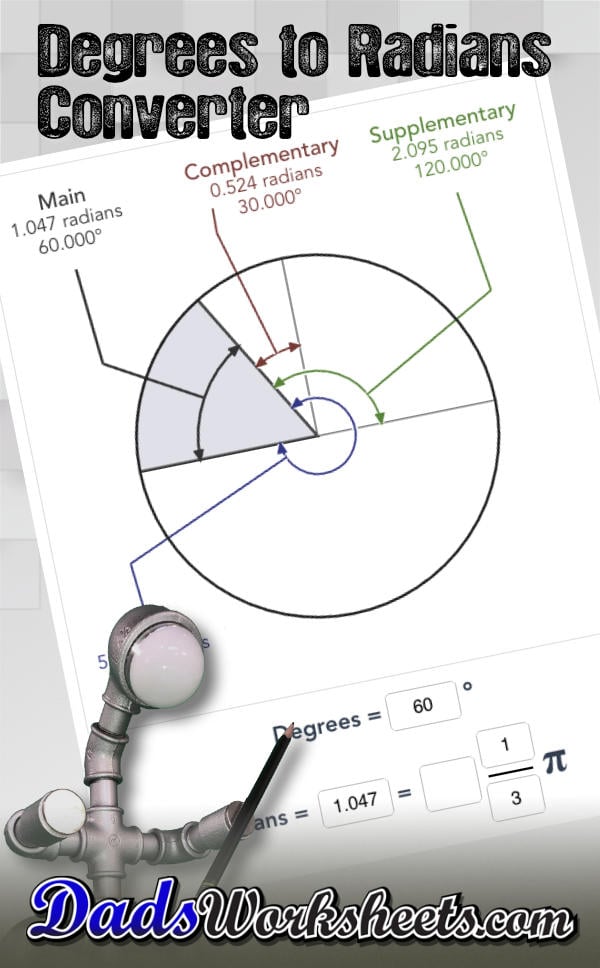
Ez a számológép fokokat radiánokká, illetve radiánokat fokokká alakít át. A számológép komplementer és kiegészítő szögeket is kiszámít, és megjeleníti a kapcsolódó szögek kombinált ábrázolását, így azok azonnal szemléltethetők. A számológép automatikusan átvált fokról radiánra, amikor új értéket ad meg.
Mi a fok?
Amikor két egyenes közötti szöget mérünk, ez a mérés megadja a szükséges elfordulás mértékét ahhoz, hogy az egyik egyenes meredeksége megegyezzen a másikéval. A fok szó a legáltalánosabb használatban “mennyiséget” jelent, de egy szög mérésekor a fok szó a forgás mértékegysége.
A kör fokai
Egy teljes fordulat (vagy fordulat) egy teljes körnek, vagyis pontosan 360 fokos forgásnak felel meg. Ha csodálkozol azon a furcsának tűnő választáson, hogy 360 fokot használnak egy teljes fordulat jelölésére, valószínűleg a babilóniaiakat hibáztathatod. Néhány ősi számrendszer olyan egységeken alapult, mint a 12 és a 60. A modern életbe átvitt példák erre a naptár 12 hónapja és a nap 24 órája (12 óra nappal, 12 óra éjszaka). Egy másik példa a 360, mint a teljes kör mértékegységének megválasztása. A 360 szépen faktorál 12-vel és 60-zal is, és egy körbe hat egyenlő oldalú háromszöget lehet beírni (amelyek mindegyik szögében pontosan 60 fok van).
Mi a radián?
Míg a fokokat a legtöbb ember ismeri, sok alkalmazásnál kényelmesebb a szögmérés egy másik mértékegységében, a radiánban dolgozni. A radián értékének megértéséhez hasznos megjegyezni a kör kerületére vonatkozó képletet…
Kör kerülete
A kerület közvetlenül kapcsolódik egy teljes körforgáshoz, és a kerület körül való utazás fogalmilag hasonlít egy pont 360 fokos elforgatásához a kör origója körül. Ha egy egységnyi sugarú kört képzelünk el (egységkör), akkor ez az út pontosan 2π egységnek felel meg. És valójában ezek a tetszőleges kerületi egységek rádiánok, és egy teljes körforgásban pontosan 2π radián van.
A forgás radiánokban való kifejezése számos más trignometriai számítást egyszerűsít, de mivel a radiánokat pi-ben fejezik ki, gyakorlati alkalmazásokban (például egy fűrészlap szögének beállítása, amikor egy fadarabot vágunk) kevésbé hasznosnak tűnhetnek. Itt jön a képbe ez a fokból radiánba átalakító!
Sugarak a körben
Ez a fokból radiánba átalakító lehetővé teszi, hogy a radiánokat vagy tízes értékként, vagy a pi törtrészeként adja meg, és megfelelően kiszámítja az alternatív radián ábrázolást, valamint a fokban megadott értéket.
Hogyan lehet fokokat radiánokká alakítani
A fokok radiánokká alakításához két egyszerű megközelítés létezik: az egyik a tizedes radiánokkal, a másik a pi törtrészeként kifejezett radiánokkal foglalkozik.
Miatt, hogy a kör fokainak száma egy traszcendens szám, és nem véges tizedes kiterjesztésű, nem létezik pontos átváltás fokokról tizedes radiánokra. Azonban ésszerű közelítés, ha egy olyan tizedes konstansot használunk, amely kellő pontosságú ahhoz a számításhoz, amit el akarunk végezni…
Fokokból radiánokká tizedes
Ha azonban a radiánokat a pi törtrészeként fejezzük ki, akkor a pi-vel szorzott pontos törtrész kiszámítható. Emlékezzünk vissza, hogy egy teljes kör (360°-os forgás) pontosan 2π radián, tehát 180° π radián. Ezért egy fok a π sugár 1/180-ad része…
A fokok sugárrá alakítása a pí törtrészeként
Ez a törtrész a fokok sugárrá alakítását egyszerű törtrész szorzási és redukciós feladattá alakítja. Ha például 36 fokot szeretnénk átváltani radiánra, az átalakítás így nézne ki…
Példa: 36 fok átváltása radiánokká
A fokok sugárrá alakítására szolgáló módszerek mindegyike hasonló, és azon az elképzelésen alapul, hogy a fok π/180 sugár.
Hogyan lehet radiánokat fokokká alakítani
A radiánok fokokká alakítása hasonló, és használhatjuk a fokok radiánokká alakításánál használt konstansok invertálását…
Radiánok fokokká
Degrees to Radians Updates
| Date | Description |
|---|---|
| 06/3/2019 | Initial version of the Degrees to Radians converter. |
| 01/29/2021 | Frissítve az új számológép formátumra. |