Fél összeadó és teljes összeadó áramkör
A fél összeadó és teljes összeadó áramkörök az igazságtáblázatukkal együtt kerülnek ismertetésre ebben a cikkben. A Full Adder tervezése a Half Adder áramkör segítségével szintén bemutatásra kerül. Az egybites teljes összeadó áramkör és a többbites összeadás a teljes összeadó használatával szintén bemutatásra kerül.
Mielőtt belemennénk ebbe a témába, nagyon fontos tudni a Boole logikáról és a logikai kapukról.
KÉPZELJÜK MEG : BOOLEUS LOGIKA
KÉPZELJÜK MEG : LOGIKAI KAPUK
KÉPZELJÜK MEG : FLIP FLOPS
Mi az összeadó?
Az összeadó egyfajta számológép, amelyet két bináris szám összeadására használnak. Amikor azt mondom, számológép, nem egy gombokkal ellátottra gondolok, ez egy olyan áramkör, amely számos más áramkörrel integrálható a legkülönbözőbb alkalmazásokhoz. Kétféle összeadó létezik;
- Fél összeadó
- Teljes összeadó
Fél összeadó
A fél összeadó segítségével olyan áramköröket tervezhetünk, amelyek logikai kapuk segítségével képesek egyszerű összeadást végezni.
Először nézzük meg az egybites összeadást.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Ezek a legkevesebb lehetséges egybites kombinációk. De 1+1 esetén az eredmény 10. Bár ez a probléma megoldható egy EXOR kapu segítségével, de ha érdekel a kimenet, az összegeredményt át kell írni 2 bites kimenetként.
Így a fenti egyenleteket így írhatjuk fel:
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Itt a ’10’ kimenet ‘1’-je lesz a carry-out. Az eredmény az alábbi igazságtáblázatban látható. A ‘SUM’ a normál kimenet, a ‘CARRY’ pedig az átvitel.
Bemenetek Kimenetek
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Az egyenletből, világosan látszik, hogy ez az 1 bites összeadó könnyen megvalósítható egy EXOR kapu segítségével a ‘SUM’ kimenethez és egy AND kapu segítségével az átvitelhez. Nézze meg az alábbi megvalósítást.
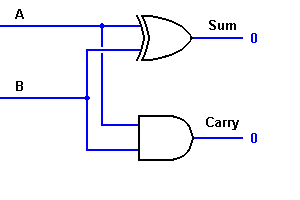
A komplex összeadásnál előfordulhat, hogy két 8 bites bájtot kell összeadni. Ezt csak teljes összeadó logika segítségével lehet megoldani.
Teljes összeadó
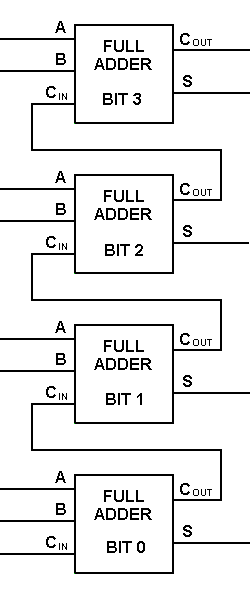
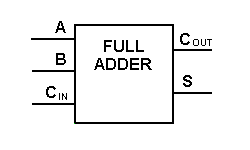
Ezt a típusú összeadót kicsit nehezebb megvalósítani, mint a fél összeadót. A fő különbség a fél-adder és a teljes-adder között az, hogy a teljes-addernek három bemenete és két kimenete van. Az első két bemenet A és B, a harmadik bemenet pedig egy CIN nevű bemeneti átvitel. Amikor egy teljes összeadó logikát tervezünk, képesek leszünk nyolcat összefűzni, hogy egy bájtnyi összeadót hozzunk létre, és a hordozóbitet kaszkádszerűen továbbítsuk egyik összeadóból a másikba.
A kimeneti hordozót COUT-nak, a normál kimenetet pedig S-nek jelöljük. Nézzük meg az igazságtáblázatot.
BEMENETEK KIMENETEK
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 0 1
0 1 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1 1
A fenti igazságból-táblázatból, a teljes összeadó logika megvalósítható. Láthatjuk, hogy az S kimenet egy EXOR az A bemenet és a fél-adder SUM kimenete között B és CIN bemenetekkel. Azt is meg kell jegyeznünk, hogy a COUT csak akkor lesz igaz, ha a három bemenet közül bármelyik két bemenet HIGH.
Így egy teljes összeadó áramkört két fél összeadó áramkör segítségével valósíthatunk meg. Az első fél összeadót A és B összeadására használjuk, hogy részleges összeget állítsunk elő. A második fél összeadó logika használható a CIN hozzáadására az első fél összeadó által előállított összeghez, hogy megkapjuk a végső S kimenetet. Ha a fél összeadó logika bármelyike hordozást eredményez, akkor lesz egy kimeneti hordozás. Így a COUT a fél-adder Carry kimenetek VAGY függvénye lesz. Nézzük meg a teljes összeadó áramkör alább látható megvalósítását.
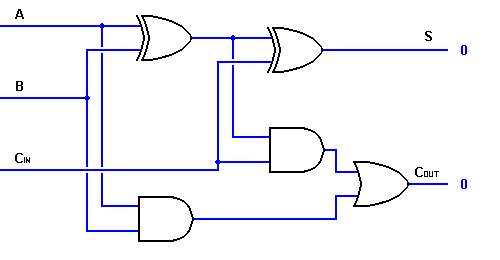
Noha a fenti teljes összeadó logikával nagyobb logikai diagramok megvalósítása is lehetséges, a művelet ábrázolására többnyire egyszerűbb szimbólumot használunk. Az alábbiakban egy egybites teljes összeadó egyszerűbb kapcsolási rajzát adjuk meg.
Egy ilyen típusú szimbólummal két bitet adhatunk össze úgy, hogy a következő alacsonyabb nagyságrendűből veszünk átvitelt, és a következő magasabb nagyságrendűbe küldünk átvitelt. A számítógépben egy többbites művelethez minden egyes bitet egy teljes összeadóval kell ábrázolni, és egyszerre kell összeadni. Így két 8 bites szám összeadásához 8 teljes összeadóra van szükség, amelyek két 4 bites blokk kaszkádolásával alakíthatók ki. Két 4 bites szám összeadása az alábbiakban látható.