Általános kémia témakörök
Energia: Alapfogalmak
Az energia formái: Mozgási és potenciális. munka és energia. hő és hőmérséklet. elektrosztatikus potenciális energia.
Energia: mozgási és potenciális
Az energia fogalma alapvető a fizikai tudományokban. Célunk itt az energiával kapcsolatos néhány első alapelv lefektetése, valamint az energia néhány olyan formájának bemutatása, amelyek különösen fontosak a kémia számára. Először is, gyakran nagyon hasznos a rendszert úgy definiálni, hogy az univerzum egy adott részét értjük alatta, amelyen megfigyeléseinket végezzük. A rendszert egy tárgy vagy tárgyak gyűjteménye alkotja, és a világegyetem többi részétől – amelyet környezetnek nevezünk – egy valós vagy képzeletbeli határvonal különbözteti meg.
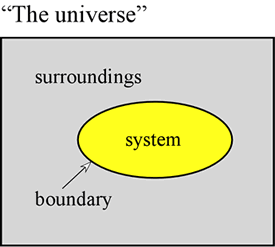
A rögzített térfogatban, például egy fémhengerben tartott gázminta egy példa a rendszerre – ez a rendszer akkor lesz számunkra fontos, amikor a gázok általános tulajdonságainak tanulmányozásával foglalkozunk. További példák a léggömb belsejében lévő gázminta vagy a dugattyúval ellátott hengerben lévő égési keverék. Mindkét esetben a rendszert egy fizikai, de mozgatható határ veszi körül, így a rendszer térfogata nem rögzített. Egy további példa, amelyet gyakran fogunk megvizsgálni, egy kémiai reakciót folytató oldott anyagkeverék egy kémcsőben vagy főzőpohárban. Az itt bevezetett terminológia különösen fontos annak tanulmányozásában, hogyan nyilvánul meg az energia a kémiai rendszerekben, ami nagyrészt a termodinamika tárgykörébe tartozik.
Az általános kémiában az általunk relevánsnak tekintett rendszerek jellemzően nyugalmi állapotban vannak, és a gravitációs hatásokat figyelmen kívül hagyjuk. Gyakran leginkább olyan rendszerek érdekelnek bennünket, amelyekben kémiai reakciók zajlanak, és a rendszer kémiai összetétele az idő múlásával változik. Egyelőre azonban fogadjunk el egy tágabb perspektívát, és használjunk mechanikai rendszereket, például egy lengő ingát vagy guruló és ütköző biliárdgolyókat, hogy segítsenek megérteni az energiával kapcsolatos általános elveket.
Egy rendszerről azt mondhatjuk, hogy kétféle módon rendelkezik energiával, amelyeket kinetikus és potenciális energiának nevezünk. A mozgási energia a mozgásban lévő anyag energiája. A fizika pontos matematikai definíciót ad a kinetikus energiára (KE), amelyet a (balra lent látható) egyenlet mutat.
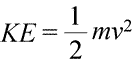
Ezben egy tárgy kinetikus energiáját a tárgy tömegének (m) és sebességének (v) négyzetével, valamint az ½ állandósággal való szorzataként ábrázoljuk. Ha a rendszer egynél több objektumból áll, a teljes kinetikus energia az egyes objektumok kinetikus energiáinak összegeként fejezhető ki.
Az energia mértékegységeit e definíció alapján tudjuk levezetni. Az energia SI-egysége a joule (J), amelyet a következőképpen határozunk meg:
1 J = 1 kg-m-s-2
A potenciális energia egy rendszer energiája, amely jellemzően valamilyen formában kinetikus energiává alakítható, és valamilyen mértékben képes a munka nevű mennyiséget előállítani (ezt alább tárgyaljuk). A potenciális energia egyértelmű példája egy tégla egy épület párkányán. A tégla bizonyos mennyiségű potenciális energiával rendelkezik a magassága – a gravitációs mezőhöz viszonyított elhelyezkedése – miatt. Ha egy lökést adunk a téglának, hogy leessen a párkányról, akkor spontán elmozdul az alacsonyabb gravitációs potenciális energia irányába, és eközben kinetikus energiát nyer. Egy másik példa az akkumulátor elektromos potenciális energiája (amelyet a feszültséggel fejezünk ki). Amikor egy vezetékkel és egy villanykörtével áramkört hozunk létre, összekötve az akkumulátor két pólusát, a köztük lévő elektromos potenciálkülönbség hatására a vezetékben lévő elektronok mozgásba lendülnek (mozgási energia), ami hő- és fénytermeléshez egyaránt vezet.
Az energiával kapcsolatban fontos általános alapelv, hogy nem lehet sem létrehozni, sem megsemmisíteni. Ezt az energiamegmaradás törvényének nevezik. Mennyiségileg ez azt jelenti, hogy egy olyan rendszerben, mint a zuhanó tégla vagy az óra ingája, a mozgási és a potenciális energia összege állandó. Ez némileg absztrakció, mivel egy valódi ingában az energia egy része a súrlódás miatt folyamatosan elvész, és egy kis energiát kell hozzáadni az ingához, hogy az lengjen (és az óra működjön). Ha azonban az ilyen “elveszett” energiát (amely valójában a környező levegőmolekulák hőenergiájának növekedéseként jelenik meg) gondos kísérleti mérésekkel figyelembe vesszük, kiderül, hogy az energia valóban mindig megmarad. Egy másik figyelmeztetés Einstein híres E = mc2 egyenletében foglalható össze, amely a tömeg és az energia alapvető ekvivalenciáját fejezi ki. Az energia megmaradásának törvényének egy általánosabb formája, amelyet a tömeg-energia megmaradásának törvényének nevezhetünk, figyelembe veszi ezt az ekvivalenciát. Visszatérve az általános kémiához, az ilyen anyag-energia átváltások jellemzően nem tartoznak a hatáskörébe, míg a magreakciók és a radioaktivitás tanulmányozása az atomfizika körébe tartozik.
Ha olyan kémiai reakciót tekintünk, amelyben a kémiai változásokat hőtermelés kíséri, felmerül egy kérdés: Mi a helyzet az energia megőrzésével ebben az esetben? A válasz az, hogy létezik a potenciális energiának egy olyan formája, amelyet kémiai potenciális energiának (vagy egyszerűen kémiai potenciálnak) nevezhetünk, és amelyről úgy gondolhatunk, hogy a reaktánsok molekuláris összetételében rejlik. Ez a potenciális energia aztán hő formájában energiává alakul át, de kiderül, hogy a jelen lévő nettó energiamennyiség állandó marad, amint képesek vagyunk meghatározni és mérni a hőtermelést. Egy mindennapi példát arra, amit ma már kémiai potenciális energiaként értelmezhetünk, a benzinmotor ad, ahol a benzin és az oxigén keveréke rendelkezik az energia látens formájával. Ez a benzin/oxigén keverékben lévő látensenergia a gépkocsi mozgási energiájának előállítására fordítódik.
Munka és energia
A munka egy másik olyan fogalom, amely a fizikában pontos definíciót enged meg. Sőt, a mechanika törvényei a munka-energia tétel segítségével összekapcsolhatók az energiával. Egy focilabda elrúgása, vagy számos hasonló példa szemlélteti azt az elképzelést, hogy egy tárgy mozgási energiája erő alkalmazásával növelhető. A munka-energia tétel, amely ennek az elképzelésnek az általánosítása, nagyjából a következőképpen fogalmazható meg: A tárgy által birtokolt energia változása egyenlő a rá ható erő nagyságának és az erő hatásának távolságával szorozva.
A munka eredményeként egy rendszerben bekövetkező energiaváltozás a rendszer szempontjából pozitív vagy negatív lehet. A munkát végezheti egy rendszer, vagy egy rendszerre a környezet végezhet munkát. Ha egy rendszer munkát végez, akkor energiát veszít a környezetnek. Ha a rendszeren munkát végeznek, akkor a rendszer energiája növekszik. Például, amikor egy mozgó dugattyúval ellátott hengerben az égési keveréket beindító szikra a rendszer gyors tágulását okozza, és a tágulás mechanikusan összekapcsolódik egy rúd mozgásával a környezetben, a henger rendszere munkát végez a környezeten, és ezáltal energiát veszít. Ez természetesen része annak, ahogyan egy belsőégésű motor a kémiai potenciális energiát a mozgásban lévő autó mozgási energiájává alakítja.
A munka-energia tétel egyik következménye az egységekre vonatkozik, nevezetesen, hogy a munka ugyanabban az egységben mérhető, mint az energia. Mivel Newton második törvénye szerint az erő = tömeg × gyorsulás, a newton (N), az erő SI-egysége az M × L × T -2, és így 1 N = 1 kg m s-2. Az erő és a távolság szorzata M × L2 × T -2, így az energia SI-egységét, a joule-t (J) 1 J = 1 kg m2 s-2 -ként határozzuk meg. Ezen a ponton meg kell győződnöd arról, hogy a mozgási energia egyenlete a tömeg (M), a hossz (vagy távolság, L) és az idő (T) alapvető mennyiségek azonos kombinációját tartalmazza.
Hő és hőmérséklet
Elég gyakran használjuk a hő és a hőmérséklet szavakat, és gyakran beszélünk a hőről mint energiaformáról. Mindannyiunknak van egy intuitív érzékünk arról, hogy mik ezek a dolgok, de itt szeretnénk tudományosabban gondolkodni róluk, és ha lehet, formálisabb definíciókat adni nekik. Ez szükséges előzménye a hőnek megfelelő energia számszerűsítésének, és onnan az energia megmaradásának törvényét igazoló méréseknek. Azt találjuk, hogy egy rendszer hőenergiája az azt alkotó atomok és molekulák teljes mozgási energiájához hasonlítható (a fenti definíció szerint). Egy tárgy vagy rendszer hőmérséklete valójában az alkotó atomok és/vagy molekulák átlagos mozgási energiájának mérőszáma. (N.B. A hőmérséklet nem pontosan egyenlő az átlagos molekuláris mozgási energiával, de egyenesen arányos vele. További részletekért lásd a kinetikus molekulaelmélet weboldalát).
Az egyik módja annak, hogy szemléltessük, mit értünk hő és hőmérséklet alatt, és a köztük lévő különbséget, a biliárdgolyó analógiája. Bizonyos egyszerű összefüggésekben a biliárdgolyók viselkedése megfelelő modellje az atomok vagy molekulák gyűjteményének, például egy gázmintának. A biliárdgolyókhoz hasonlóan, amelyeket éppen egy gyorsan mozgó biliárdgolyó ütött meg, a gázmolekulák is mindenfelé mozognak, egymásnak és az őket tartalmazó tartály falának pattognak. A biliárdgolyók teljes mozgási energiája, amely nem más, mint az egyes golyók egyedi mozgási energiáinak összege, analóg a gázmolekulákból álló minta hőenergiatartalmával. A biliárdjáték kezdetén bekövetkező “szünetben” a dákógolyó kezdeti mozgási energiája az asztalon lévő összes golyó között eloszlik. Néhányan elég gyorsan mozognak, mások pedig nem olyan gyorsan, de a “hő” vagy “hőenergia” analógiája a biliárdgolyók rendszerére nézve csak ezeknek a kinetikus energiáknak az összege. Másrészt a biliárdgolyórendszer hőmérséklete arányos lenne a golyók együttesének átlagos mozgási energiájával.
Elektrosztatikus potenciális energia
Az elektrosztatikus vonzás és taszítás törvénye vagy Coulomb-törvény azt az erőt írja le, amelyet egy töltött tárgyra egy másik töltött tárgy jelenléte gyakorol. Az erő akkor számítható ki a legkönnyebben, ha a töltések nagyon kis ponttöltésekként kezelhetők. A töltött tárgy által “érzett” erő nagysága arányos a töltések szorzatával (az elektromos töltés SI-egysége a Coulomb, C), és fordítottan arányos a töltések közötti távolság négyzetével (r a jobb oldali ábrán). Az erő vonzó erő (a gravitációhoz hasonlóan, az ábrán befelé mutató nyílhegyekkel jelölve), ha a töltések előjele ellentétes, és taszító, ha a töltések előjele azonos.
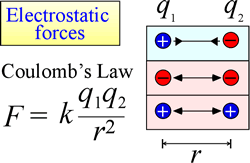
Ha az erő (például az elektrosztatikus, mágneses és gravitációs erő) távolról (a téren keresztül, mechanikai érintkezés nélkül) is hathat, az ilyen erőknek kitett tárgyakat potenciális energiamezőben lévőnek mondjuk. Fentebb beszéltünk a gravitációs potenciális energiáról, és hasonlóan az elektrosztatikus erők esetében is, egy töltött tárgy elektrosztatikus potenciális energiával rendelkezik, mivel elektromos mezőben helyezkedik el. Ilyen mező bármely más töltés vagy töltések közelében létezik.
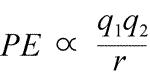
Az elektrosztatikus potenciális energia egyenlete: A PE arányos a q1 és q2 töltésekkel, és fordítottan arányos az elválasztási távolsággal, r. A potenciális energiafüggvény alakja matematikailag az erőkifejezésből, a Coulomb-törvényből következik.
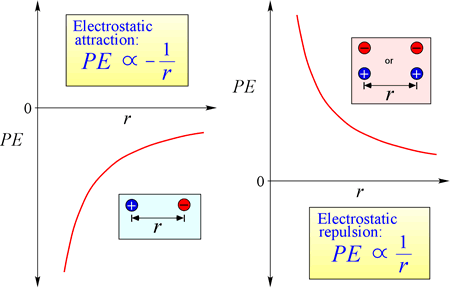
A vonzásban lévő töltések ellentétes előjelét tekintve a potenciális energia mindig negatív, és minél közelebb kerülnek egymáshoz a töltések, annál negatívabb – azaz annál kisebb – lesz a potenciális energia. Ahogy az elválasztási távolság, r a nullához közelít, a potenciális energia végtelenül negatív lesz. Azonos előjelű töltések esetén a taszítás energiája mindig pozitív, és végtelenül pozitív lesz, ahogy az elválasztási távolság, r a nullához közelít.
Az elektrosztatikus potenciális energia fontos szempont a kémiában. Az atom természetének, a kémiai kötésnek és a molekulák közötti erőknek a megértése feltétlenül függ a rendszer energiájához hozzájáruló töltés-töltés kölcsönhatások hatásának figyelembevételétől.
Fontos mértékegységek
Energia (SI-egység) 1 joule = 1 J = 1 kg-m-s-2
Elemi töltés, e = 1,60218 × 10-19 C (coulomb, C)
Faraday-állandó: F = NAe = 9,64853 × 104 C-mol-1
Elektromos potenciál: Volt, V 1 V = 1 J C-1