Kezdjük az értékek exponensekkel való osztásának vizsgálatával.
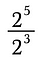
Emlékezzünk arra, hogy az exponensek ismételt szorzást jelentenek. Tehát a fenti kifejezést átírhatjuk így:
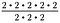
Mivel 2/2 = 1, töröljünk ki három 2/2-es sorozatot. Így marad 2 – 2, vagyis 2 négyzetben.
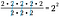
Lehet persze rövidíteni, és kivonhatjuk az alul lévő 2-esek számát a felül lévő 2-esek számából. Mivel ezeket a mennyiségeket a megfelelő exponensekkel ábrázoljuk, csak annyit kell tennünk, hogy a közös bázist írjuk fel az exponensértékek különbségének hatványaként.
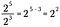
Ha ezt a szabályt általánosítjuk, akkor a következőt kapjuk, ahol n egy nem nulla valós számot jelöl, és x és y szintén valós számok.
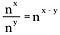
A nullapotenciál feltárása
Ezzel könnyen levezethető a magyarázat arra, hogy miért egyenlő bármely nullától eltérő szám nullapotenciálra emelve 1-gyel. Ismét nézzünk egy konkrét példát.
Tudjuk, hogy bármely nem nulla szám önmagával osztva egyenlő 1-gyel. Tehát leírhatom a következőt:
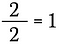
Ez ugyanaz, mintha leírnánk:
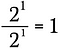
Most felhasználom a fenti exponensszabályt, hogy átírjam ennek az egyenletnek a bal oldalát.
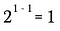
Ez természetesen egyenértékű a következőkkel:
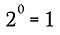
Ezzel az eljárással és a fenti általánosított szabállyal együtt megmutathatjuk, hogy bármely nem nulla valós szám nulladik hatványára emelve 1-et kell kapnunk.
Mi a helyzet a nullával a nulla hatványáig?
Ez az a pont, ahol a dolgok bonyolulttá válnak. A fenti módszer megszakad, mert természetesen a nullával való osztás nem lehet. Vizsgáljuk meg, hogy miért.
Kezdjük azzal, hogy megnézünk egy gyakori nullával osztás HIBÁT.
Hogyan van a 2÷0? Nézzük meg, miért nem tehetjük ezt meg.
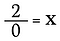
Az osztás valójában csak a szorzás egy formája, tehát mi történik, ha a fenti egyenletet átírom így:
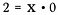
Melyik lehetséges érték elégítheti ki ezt az egyenletet x számára?
Nincs ilyen érték! Bármely szám szorozva nullával nullát eredményez, soha nem lehet egyenlő 2-vel. Ezért azt mondjuk, hogy a nullával való osztás meghatározatlan. Nincs lehetséges megoldás.
Most nézzük meg a 0÷0-t.
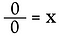
Még egyszer írjuk át szorzási feladatként.
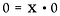
Itt egy egészen más helyzettel találkozunk. Az x megoldása MINDEN valós szám lehet! Nincs mód arra, hogy meghatározzuk, hogy mi az x. Ezért a 0/0 határozatlannak* tekinthető, nem pedig meghatározatlannak.
Ha a fenti módszerrel, nullával mint bázissal próbáljuk meghatározni, hogy mi lenne a nulla a nulla hatványára, azonnal megállunk, és nem folytathatjuk, mert tudjuk, hogy 0÷0 ≠ 1, de határozatlan.
Mivel egyenlő tehát a nulla a nulla hatványára?
Ez erősen vitatott. Egyesek szerint 1-ben kell definiálni, míg mások szerint 0, és vannak, akik szerint meghatározhatatlan. Mindegyik mellett vannak jó matematikai érvek, és talán az a leghelyesebb, ha meghatározatlannak tekintik.
Mindezek ellenére a matematikai közösség amellett van, hogy a nullát nullapotenciálra 1-ként definiáljuk, legalábbis a legtöbb célra.
Az amatőr matematikus számára talán hasznos az exponensek definíciója a következő: