
Soha ne oszd el nullával. Ezt mindannyian tanultuk az iskolában, és a legtöbb hétköznapi helyzetben ez egy jó tanács. Ritkán van értelme bármit is nullával osztani, és ha megpróbálod megkérni Sirit, hogy tegye meg, azt fogja mondani, hogy nincsenek barátaid.
De pontosan miért is olyan rossz ötlet nullával osztani? És vannak olyan esetek, amikor a nullával osztás jó dolog lehet? Ha nem figyeltél oda a középiskolában, egy gyors felfrissítés felnyithatja a szemed a matematika számos csodájának egyikére.
A nullával osztásnak nincs értelme, mert a számtanban a nullával való osztás nullával való szorzásként is értelmezhető. A 3/0=X ugyanaz az egyenlet, mint a 0*X=3. Nyilvánvalóan nincs olyan szám, amit X helyére be lehet dugni, hogy ez az egyenlet működjön.
A hasonló helyzetet eredményez, ha megpróbálod a nullát önmagával osztani. A 0/0=X átírható 0*X=0-nak, és itt az a probléma, hogy minden szám működik. X bármi lehet, így ez az egyenlet nem túl hasznos.
De vannak olyan esetek, amikor a nullával való osztás valóban működik, és valójában elengedhetetlen a probléma megoldásához. Ez volt Newton felismerése, amikor feltalálta a számítást.
Tegyük fel például, hogy van egy görbénk, és meg akarjuk találni az alatta lévő görbe meredekségét egy adott pontban. Ez ugyanaz, mintha egy olyan egyenes meredekségét próbálnád megtalálni, amely csak az adott ponton érinti a görbét, ezt nevezzük érintővonalnak. Sok esetben lehetetlen megtalálni ezt a meredekséget pusztán az algebra segítségével.
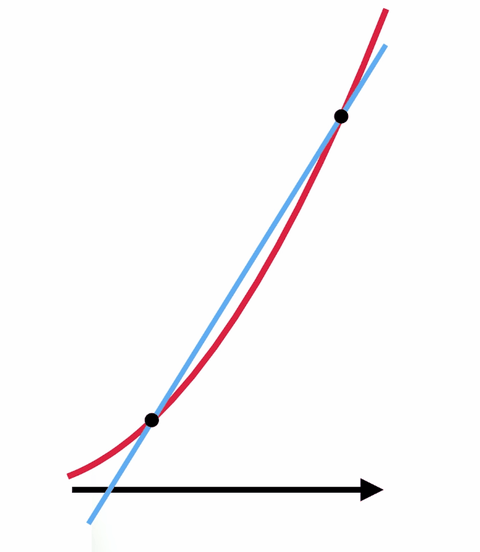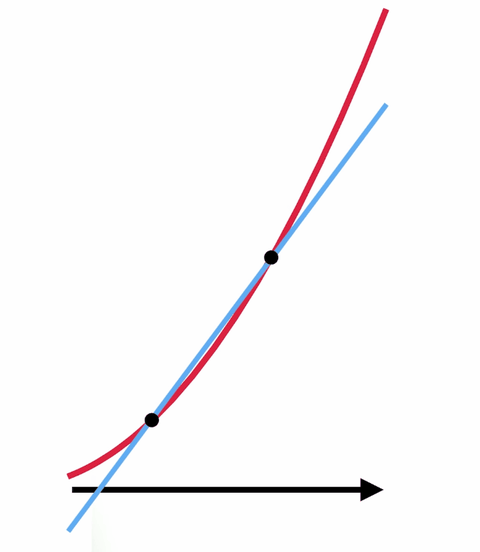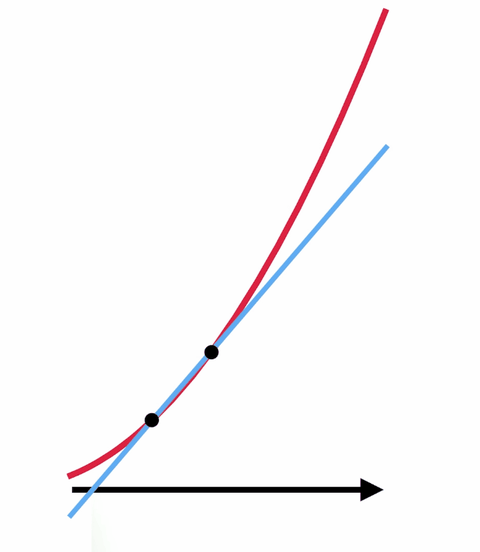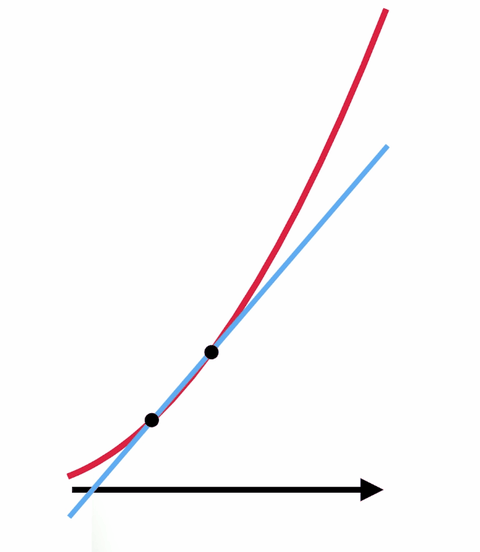

De van egy trükk, ami a számítást és a nullával való osztás varázslatát használja. Az érintővonal megtalálása helyett sokkal egyszerűbb, ha egy olyan egyenes meredekségét keressük meg, amely két ponton érinti a görbét. Ha ezt a két pontot egyre közelebb és közelebb helyezzük egymáshoz, akkor egy olyan egyenest kapunk, amely közel áll a kívánthoz.
Ha a két pontot úgy mozgatod, hogy egymás fölé kerüljenek – úgy, hogy gyakorlatilag csak egy van -, akkor megkapod az eredetileg kívánt érintővonalat, csak ezúttal a meredekséget is meg tudod találni. Lényegében nullát osztasz önmagával, és megkapod a választ.
A nullával való osztás trükkje lényegében abban áll, hogy létrehozol némi extra összefüggést. A 0/0-val az a kezdeti probléma, hogy minden szám potenciálisan válasz lehet, így néhány korlátozó tényező bevezetésével leszűkíthetjük a lehetséges válaszokat.
És ha már tudsz nullával osztani, a matematika egy teljesen új világa nyílik meg. A nullákkal, végtelenségekkel és mindenféle lehetetlen egyenletekkel való játék mindennapossá válik. Tanulj meg nullával osztani, és a matematika soha többé nem lesz ugyanaz.