A kvadratikus egyenlet 101 alkalmazása

Nem gyakran fordul elő, hogy egy matematikai egyenlet bekerül az országos sajtóba, még kevésbé a népszerű rádióba, vagy ami a legmeglepőbb, hogy a brit parlamentben vita tárgyát képezi. 2003-ban azonban a jó öreg kvadratikus egyenlet, amelyről mindannyian tanultunk az iskolában, mindezek közé tartozott.

Hol kezdjük

Az egész a Tanárok Nemzeti Szakszervezetének egyik ülésén kezdődött. A kvadratikus egyenletet a nemzet elé tartották, mint a matematikusok által a szegény gyanútlan iskolásoknak okozott kegyetlen kínzás példáját. A vádaskodás hatására a kvadratikus egyenlet főszerepet vállalt a főműsoridőben sugárzott rádióban, ahol egy félelmetes interjúkészítő kérdezte, aki inkább a miniszterelnökkel szokott szembeszállni. A (londoni) Times vezető rovatában, amelyet általában a modern világ erkölcsi (vagy egyéb) egészségéről szóló súlyos vitáknak tartanak fenn, azt hirdette, hogy a kvadratikus egyenlet haszontalan, a matematika haszontalan, és hogy senki sem akar matematikát tanulni, tehát minek törődjön vele. Aggódva amiatt, hogy a kvadratikus egyenlet veszélyes beismerései megkérdőjelezhetetlenek maradnak, a brit alsóházban megvitatták az egyenlet létfontosságú jelentőségét az Egyesült Királyság fennmaradása szempontjából (pozitív véleményt fogalmaztak meg, örülhetnek, ha tudják).

Hová vezetne mindez? A kvadratikus egyenlet valóban halott volt? Érdekelt ez valakit? A matematikusok tényleg gonosz szörnyetegek, akik csak azért akarják a kvadratikus egyenleteket a fiatalabb generációra kényszeríteni, hogy megrontják halhatatlan lelküket?

Meglehet, de ez nem igazán a kvadratikus egyenlet hibája. Valójában a kvadratikus egyenlet kulcsszerepet játszott nemcsak az egész emberi civilizációban, ahogy mi ismerjük, hanem más idegen civilizációk lehetséges felderítésében, sőt még olyan létfontosságú modern tevékenységekben is, mint a műholdas televíziózás. Az isteni kinyilatkoztatás természetén kívül mi másnak lehetett volna ekkora hatása az általunk ismert életre? Valóban, nagyon is valóságos értelemben a kvadratikus egyenletek megmenthetik az életünket.”

A babilóniaiak

Az egész a babilóniaiakkal kezdődött i. e. 3000 körül. Ők voltak a világ egyik első civilizációja, és olyan nagyszerű ötletekkel álltak elő, mint a mezőgazdaság, az öntözés és az írás. Megrajzolták a Nap, a Hold és a bolygók útját, és ezeket agyagtáblákra jegyezték fel (amelyek ma is megtekinthetők a British Museumban). A babilóniaiaknak köszönhetjük a szöggel kapcsolatos modern elképzeléseket, beleértve azt is, hogy a kört 360 fokra osztották fel (egy kis számítási hibának köszönhetően, minden napra jut egy). Ugyancsak a babilóniaiaknak köszönhetjük a (rettegett) adóhivatal meglehetősen kevésbé kellemes találmányát. És ez volt az egyik oka annak, hogy a babiloniaknak négyzetes egyenleteket kellett megoldaniuk.

Tegyük fel, hogy ön egy babiloni földműves. Valahol a gazdaságodban van egy négyzet alakú mező, amelyen valamilyen terményt termesztesz. Mennyi terményt tudsz termeszteni a mezőn? Ha megduplázod a mező mindkét oldalának hosszát, akkor azt találod, hogy négyszer annyi terményt tudsz termeszteni, mint korábban. Ennek az az oka, hogy a terményből termeszthető mennyiség arányos a mező területével, ami viszont arányos az oldal hosszának négyzetével. Matematikailag kifejezve, ha a mező oldalának hossza, akkor 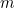a termés mennyisége, amit egy 1 oldalhosszúságú négyzet alakú mezőn termeszthetünk, és a termés mennyisége, amit termeszthetünk, akkor

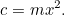Ez az első négyzetes egyenletünk, meztelenül és a napfényben pislogva. A kvadratikus egyenletek és a területek úgy kapcsolódnak egymáshoz, mint testvérek egy családban. Egyelőre azonban nem kell megoldanunk semmit – egészen addig, amíg meg nem érkezik az adóellenőr! Vidáman azt mondja a gazdának: “Azt akarom, hogy adj nekemterményt, hogy kifizessem a gazdaságod adóját”. A gazda most dilemmába kerül: mekkora földre van szüksége ahhoz, hogy ekkora mennyiségű terményt termeljen? Ezt a kérdést mi könnyen meg tudjuk válaszolni, sőt

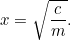A négyzetgyök megtalálása számológép segítségével számunkra könnyű, de a babiloniaknak nagyobb problémát jelentett. Ők ugyanis kifejlesztettek egy olyan módszert a válasz szukcesszív közelítésére, amely megegyezik azzal az algoritmussal (Newton-Raphson-módszer néven), amelyet a modern számítógépek a négyzetes egyenleteknél sokkal nehezebb problémák megoldására használnak.

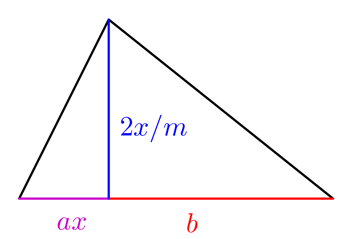
Nos, nem minden mező négyzetes. Tegyük most fel, hogy a gazdának van egy furcsább alakú szántóföldje, amelynek két háromszög alakú része van, ahogy a jobb oldalon látható.

és 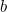megfelelő értékei esetén az a termésmennyiség, amelyet a gazda ezen a mezőn termeszteni tud, a

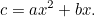Ez sokkal inkább hasonlít az általunk megszokott négyzetes egyenletre, és még az adómester gonosz szeme alatt is sokkal nehezebb megoldani. A babilóniaiak mégis újra előálltak a válasszal. Először is osztunk -val, hogy megkapjuk

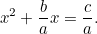Most pedig kiegészítjük a négyzetet azzal, hogy

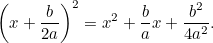Ha ezt az eredeti egyenlethez kapcsoljuk, akkor

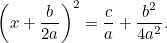Ez már egy olyan egyenlet, amit négyzetgyökvonással megoldhatunk. Az eredmény a híres “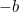 képlet”:

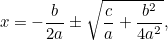ami átírható a következőképpen

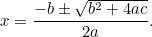(A képlet általában a “-4ac”, mert a kvadratikus egyenletet általában “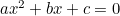” alakban szokták felírni.)

Az a tény, hogy a négyzetgyök kivétele pozitív vagy negatív választ adhat, ahhoz a figyelemre méltó eredményhez vezet, hogy a kvadratikus egyenletnek két megoldása van. Ennyit arról, hogy a matematikai rejtvényeknek csak egy megoldása van!

Nocsak, itt gyakran megáll a kvadratikus egyenletek tanítása. Elérkeztünk ahhoz a tárgyhoz, amit minden újságíró imád, amikor matematikusokat interjúvol – egy képlethez. Végtelen sok olyan kérdést lehet kitalálni, amelyekben a 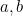és értékeket kell beírni a képletbe, hogy (két) választ kapjunk. De a matematika egyáltalán nem erről szól. A képlet megtalálása csak az első lépés egy hosszú úton. Meg kell kérdeznünk, hogy mit jelent a képlet; mit árul el nekünk a világegyetemről; valóban számít-e a képlet megléte? Lássuk most, hová vezet minket ez a képlet.

A görögök meglepetése, egy kis matematikai origami és arányérzék

Most 1000 évet gyorsítunk előre az ókori görögökhöz, és megnézzük, mit alkottak a négyzetes egyenletekből. A görögök kiváló matematikusok voltak, és a ma is használt matematika nagy részét felfedezték. Az egyik egyenlet, amelynek megoldása érdekelte őket, az (egyszerű) kvadratikus egyenlet

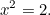Tudták, hogy ennek az egyenletnek van megoldása. Ez ugyanis egy olyan derékszögű háromszög hipotenúzájának a hossza, amelynek az oldalai egy hosszúságúak voltak.

Püthagorasz tételéből következik, hogy ha egy derékszögűszögű háromszögnek rövidebb oldalai és és hipotenzusa , akkor

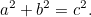Ha a 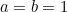és oldalakat teszem, akkor 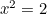. Tehát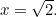

Mi tehát ebben az esetben? Vagy, hogy feltegyük a görögök kérdését, milyen szám ez? Az ok, amiért ez számított, a görögök arányérzékében rejlett. Úgy vélték, hogy minden szám arányban áll egymással. Pontosabban ez azt jelentette, hogy minden szám 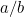alakú tört, ahol és egész számok. Az olyan számok, mint az 1/2, 3/4 és 355/113 mind példák a törtekre. Természetes volt, hogy a is tört. A hatalmas meglepetés az volt, hogy nem az. Valójában

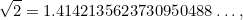, ahol a pontok azt jelentik, hogy a tizedesvégi bővítése a végtelenségig folytatódik minden felismerhető minta nélkül. (Ezzel a helyzettel később még találkozunk, amikor a káoszról tanulunk.)

volt az első irracionális szám (vagyis olyan szám, amely nem tört vagy racionális), amelyet ekként ismertek el. További példák: 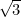,,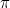 és tulajdonképpen a “legtöbb” szám. Egészen a 19. századig tartott, mire megfelelő módon tudtunk gondolkodni ezekről a számokról. Az a felfedezés, hogy a nem racionális szám, egyszerre okozott nagy izgalmat (100 ökröt áldoztak fel emiatt) és nagy megdöbbenést, a felfedezőnek öngyilkosságot kellett elkövetnie. (Legyen ez szörnyű figyelmeztetés a matematikára fogékonyaknak!) Ekkor a görögök feladták az algebrát, és a geometria felé fordultak.

Távolról sem egy ismeretlen szám, a számmal rendszeresen találkozunk: akárhányszor használunk egy darab A4-es papírt. Európában a papír méretét A méretekben mérik, az A0 a legnagyobb, területe 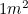. Az A méretek között különleges kapcsolat áll fenn. Ha most egy kis origamit csinálunk, fogunk egy A1-es papírlapot, majd félbehajtjuk (a leghosszabb oldala mentén), akkor A2-es papírt kapunk. Ha ismét félbehajtjuk, A3-as papírt kapunk, majd ismét A4-eset stb. A papír azonban úgy van kialakítva, hogy az egyes A méretek arányai azonosak legyenek – vagyis minden papírdarab ugyanolyan alakú legyen.

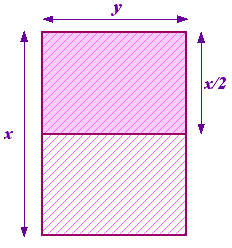
Feltehetjük a kérdést, hogy milyen arányról van szó. Kezdjünk egy olyan papírdarabbal, amelynek oldalai x és y, ahol x a leghosszabb oldal. Most ezt osszuk ketté, hogy kapjunk egy másik papírdarabot, amelynek oldalai y és x/2, és most y a leghosszabb oldal. Ezt a jobb oldali ábra szemlélteti.

Az első papírdarab arányai 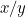, a másodiké pedig 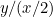vagy 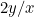. Azt akarjuk, hogy ez a két arány egyenlő legyen. Ez azt jelenti, hogy

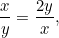vagy

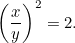Egy újabb négyzetes egyenlet! Szerencsére ez egy olyan, amivel már találkoztunk. Megoldva azt találjuk, hogy

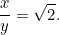Ezt az eredményt könnyű ellenőrizni. Csak vegyél egy A4-es (vagy A3-as vagy A5-ös) papírlapot, és mérd meg az oldalakat. Az egyes lapok méretét is kiszámolhatjuk. Egy A0 papírlap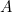területét

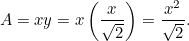De tudjuk, hogy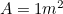tehát van egy másik négyzetes egyenletünk A0 leghosszabb oldalára,

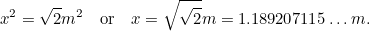Ez azt jelenti, hogy A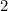leghosszabb oldalát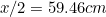adja (miért?) és A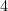oldalát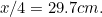adja. Ellenőrizzétek ezeket a saját papírlapotokon.

Az Egyesült Államokban használt, foolscapnak nevezett papírnak más az aránya. Hogy lássuk, miért, térjünk vissza a görögökhöz és egy másik kvadratikus egyenlethez. Miután ekkora bánatot okozott, a kvadratikus egyenlet megváltja magát a tökéletes arányok keresésében: ez a keresés ma is folytatódik a filmdíszletek tervezésében, és a természet számos aspektusában megfigyelhető.

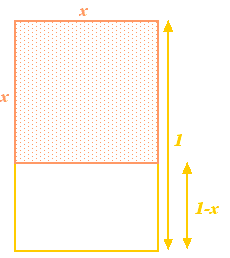
Kezdjünk egy téglalapból, majd vegyünk ki belőle egy négyzetet, amelynek oldalhossza megegyezik a téglalap legrövidebb oldalával. Ha a téglalap leghosszabb oldala 1 hosszúságú, a legrövidebb oldala pedig hosszúságú, akkor a négyzet oldalainak hossza . Ha eltávolítjuk a téglalapból, akkor egy kisebb téglalapot kapunk, amelynek leghosszabb oldala , legkisebb oldala pedig 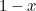. Eddig ennyire absztrakt. A görögök azonban úgy vélték, hogy a legesztétikusabb arányokkal rendelkező téglalap (az úgynevezett Arany Téglalap) az, amelynél a fentiekben megkonstruált nagy és kis téglalapok arányai megegyeznek. Ehhez az kell, hogy

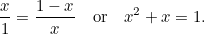Ez egy újabb négyzetes egyenlet: egy nagyon fontos egyenlet, amely mindenféle alkalmazásban előkerül. Ennek (pozitív) megoldása

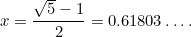A számot aranymetszésnek nevezik, és gyakran a görög 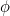betűvel jelölik.

Az aranytéglalapot az ablakok alakjában láthatjuk, különösen a grúz korabeli házakon. Újabban az aranymetszés a fényképek és filmképek “tökéletes formájaként” is megtalálható. A kvadratikus egyenlet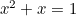felbukkan a nyulak populációinak vizsgálatában és a napraforgó magjainak és a növények szárán lévő levelek elrendeződésének mintázatában is. Mindezek a Fibonacci-sorozaton keresztül kapcsolódnak az aranymetszéshez, amelyet a

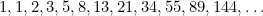Napraforgómagok adnak, Fibonacci-számokkal elrendezve

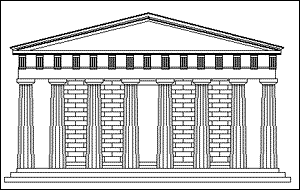
A Parthenon, az aranymetszés megtestesítője

Ebben a sorozatban minden tag az előző két tag összege. Fibonacci fedezte fel a 15. században, amikor megpróbálta megjósolni a nyulak jövőbeli populációját. Ha az egyes tagok és az utánuk következő tagok arányát vesszük, akkor a

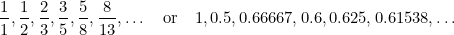számsort kapjuk, és ezek a számok egyre közelebb kerülnek (kitaláltad) az 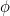aranymetszéshez.

A fenti kvadratikus egyenlet mindkét gyökét megtalálva tulajdonképpen megtalálhatjuk a Fibonacci-sorozat n-edik tagjának képletét. Ha a 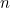-ik ilyen szám 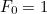és 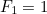mellett, akkor a

képlet szerint adódik.

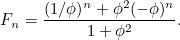A kónikusok a kvadratikus egyenleteket a csillagokhoz kapcsolják

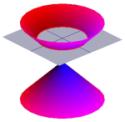
A görögöket a kúpok alakja is nagyon érdekelte. A bal oldali kép egy tipikus kúpot mutat.

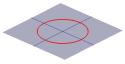
A kúp felét úgy lehet elképzelni, mint a fáklyából érkező fény terjedését. Nos, ha egy fáklyát egy sík felületre, például egy falra világítunk, akkor különböző alakzatokat fogunk látni, ahogy a fáklyát mozgatjuk. Ezeket az alakzatokat kúpszelvényeknek nevezzük, és azok a görbék, amelyeket akkor kapunk, ha a kúpot különböző szögekben szeleteljük. A görögök pontosan ezeket a görbéket tanulmányozták, és felismerték, hogy alapvetően négyféle kúpszögmetszet létezik. Ha egy vízszintes metszetet veszünk a kúpon, akkor egy kört kapunk. Ha a vízszinteshez képest kis szöget zárunk be, akkor ellipszist kapunk. Ha függőleges metszetet veszünk, akkor hiperbolát kapunk, ha pedig a kúp egyik oldalával párhuzamos metszetet veszünk, akkor parabolát kapunk. Ezeket a görbéket az alábbiakban szemléltetjük.

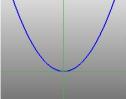
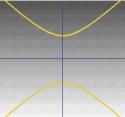
A kereszt-Kúp keresztmetszete lehet egy kör ….	… egy ellipszis …	… egy parabola …	…. vagy hiperbola.

Konikus szakaszok azért kerülnek a történetünkbe, mert mindegyiküket egy-egy kvadratikus egyenlet írja le. Különösen, ha 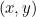az egyes görbék egy-egy pontját jelenti, akkor egy kvadratikus egyenlet köti össze és 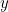görbéket. Megvan:

A kör: ;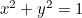

Az ellipszis: ;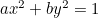

A hiperbola: ;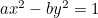

A parabola: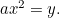

Ezeket a görbéket már a görögök óta ismerték és tanulmányozták, de a körön kívül úgy tűnt, hogy gyakorlati alkalmazásuk nincs. Amint azonban a Plusz következő számában látni fogjuk, a kvadratikus egyenletek és a kúpok közötti kapcsolat, egy hatalmas szerencsével párosulva, a világegyetem működésének megértéséhez vezetett, és a 16. században eljött az idő, amikor a kúpok megváltoztatták a világot.

A szerzőkről

Chris Budd a Bath-i Egyetem Matematikai Tudományok Tanszékének alkalmazott matematika professzora, valamint a londoni Royal Institution matematikai tanszékvezetője.

Chris Sangwin a Birminghami Egyetem Matematikai és Statisztikai Tanszékének munkatársa. Ő a Learning and Teaching Support Network Centre for Mathematics, Statistics, and Operational Research kutatója.

A közelmúltban írták a népszerű Mathematics Galore! című matematikai könyvet, amelyet az Oxford University Press adott ki.

Ezt a cikket részben a brit alsóházban a kvadratikus egyenletekről folytatott figyelemre méltó vita ihlette. A vita jegyzőkönyve megtalálható a Hansard, United Kingdom House of Commons, 2003. június 26, Columns 1259-1269, 2003, amely online elérhető a House of Commons Hansard Debate honlapján.