A 3×3-as mátrix determinánsának standard képlete a kisebb 2×2-es determinánsproblémákból áll, amelyek nagyon könnyen kezelhetők. Ha felfrissítésre van szükséged, nézd meg a másik leckémet arról, hogyan találjuk meg egy 2×2 mátrix determinánsát. Tegyük fel, hogy adott egy A négyzetes mátrix, ahol,
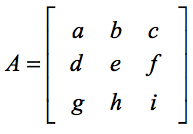
Az A mátrix determinánsa a következőképpen számítható ki:
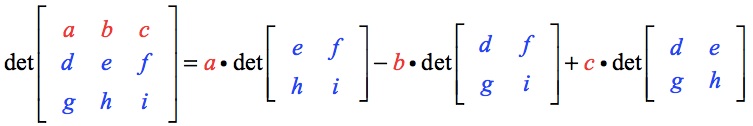
Itt vannak a legfontosabb pontok:
- Megjegyezzük, hogy a felső sor elemei, azaz a, b és c skaláris szorzóként szolgálnak egy megfelelő 2×2 mátrixhoz.
- A skalár a-t az a-n áthaladó függőleges és vízszintes vonalszakaszok rajzolásakor keletkező maradék elemek 2×2-es mátrixával szorozzuk.
- Ugyanezt az eljárást alkalmazzuk a b és c skalárszorzók 2×2-es mátrixainak felépítéséhez.
3×3 mátrix determinánsa (animált)

Példák a 3×3 mátrix determinánsának megtalálására
1. példa: Keressük meg az alábbi 3×3 mátrix determinánsát.
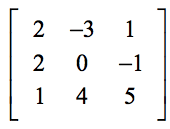
Az alábbi felállás segít megtalálni a képlet általános elemei és a tényleges feladat elemei közötti megfelelést.
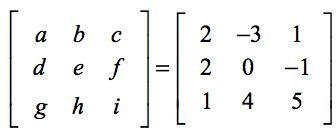
A képletet alkalmazva,


Példa 2: Értékeljük ki az alábbi 3×3 mátrix determinánsát.
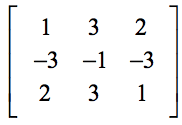
Legyen nagyon óvatos az értékek megfelelő helyekre való behelyettesítésénél a képletben. Gyakori hibák akkor fordulnak elő, amikor a tanulók az értékek behelyettesítésének kezdeti lépésénél figyelmetlenek lesznek.
Ezeken kívül szánj időt arra is, hogy meggyőződj arról, hogy a számolásod is helyes. Ellenkező esetben egyetlen hiba valahol a számításban a végén rossz választ eredményez.
Mivel,
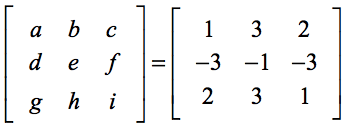
a determináns kiszámítása a következő lesz…

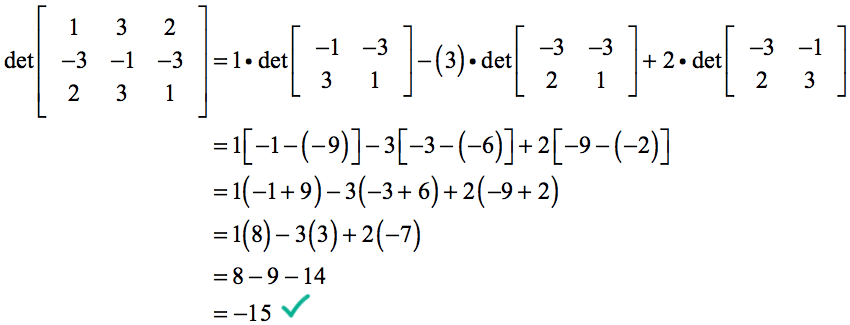
Példa 3: Oldjuk meg az alábbi 3×3 mátrix determinánsát.
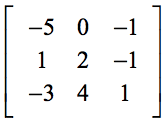
Az első sorban lévő nulla (0) jelenléte nagyban megkönnyíti számításunkat. Ne feledjük, hogy az első sorban lévő elemek skaláris szorzóként viselkednek. Ezért a nulla bármivel megszorozva azt eredményezi, hogy az egész kifejezés eltűnik.