Yksi tärkeä kysymys on, miten alkuluvut jakautuvat kokonaislukujen kesken? Vastaus on hyvin lyhyesti sanottuna melko satunnaisesti, kun otetaan huomioon tietyt perustilastot…
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Kanada
Sähköposti Bill Casselman
| |
|
Esittely
Monet vuodet sitten arveltiin, että on olemassa äärettömän monta alkulukuparia $p$, $q$, joiden kohdalla on päinvastoin $q = p+2$. Tässä ongelmassa on viime aikoina tapahtunut jonkin verran (ja kuuluisaa) edistystä. Kerron vain vähän viimeaikaisesta edistyksestä, mutta keskustelen sen sijaan siitä, mitä odotamme – pikemminkin kuin siitä, mitä tiedämme – tällaisista pareista. Mikään sanomani ei ole uutta, ja olen jossain määrin vain tarkentanut sitä, mitä Andrew Granville sanoo hiljattain ilmestyneessä huomautuksessaan viimeaikaisista edistysaskelista.
Miten monta alkulukua odotamme?
Ensimmäinen alkuluku on positiivinen kokonaisluku, jolla ei ole muita jakajia kuin itsensä ja $1$. Määritelmä on yksinkertainen, mutta heti kun aletaan tutkia alkulukujen merkitystä, huomataan, että ne käyttäytyvät paljon hienovaraisesti. Yksi tärkeä kysymys on, miten alkuluvut jakautuvat kokonaislukujen kesken. Vastaus on lyhyesti sanottuna melko satunnaisesti, kun otetaan huomioon tietyt perustilastot. Mitä tarkoitan tällä?
Noh, tässä on neliönmuotoinen joukko, joka kuvaa kaikkia alkulukuja $400$ asti:

Tässä joukossa on joitakin kuvioita, joista joitakin kommentoin myöhemmin. Suurin osa havaitsemistasi johtuu jostain näytön artefaktista. Esimerkiksi joka toinen sarake on periaatteessa tyhjä, ja tämä johtuu siitä, että ainoa parillinen alkuluku on $2$. Myös joka viides sarake on pohjimmiltaan tyhjä. Mielenkiintoisempia ovat kaksoisprimaparit (joista osa ei näy niin hyvin, koska ne jakautuvat kahdelle riville, kuten $59$, $61$), ja myös eräät viimeisiin näytettyihin numeroihin liittyvät kuviot. Näitä voidaan kutsua paikallisiksi kuvioiksi. Maailmanlaajuisia kuvioita ei ole havaittavissa.
Erittäin tehokkaisiin tapoihin tuottaa alkulukuja on panostettu paljon, mutta nykyään jopa hyvin yksinkertaisella ohjelmalla menee vain vähän aikaa suurten alkulukuluetteloiden tekemiseen. Yksi hedelmällisimmistä ohjelmista tekee suuren listan alkuluvuista ja laskee sitten sen avulla funktiolla $\pi(n)$ alkulukujen lukumäärän $\le n$.
Yksi asia, johon tätä voidaan käyttää, on saada karkea käsitys alkulukujen yleisyydestä. Alueella $$ on $135$ alkulukuja:
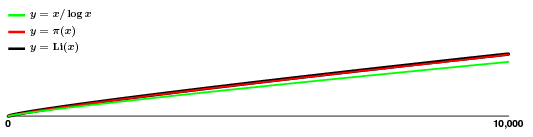
Approksimaatio näyttää hyvältä! Vaikka $\pi(x)$ siis pomppii hieman ympäriinsä, ilmeisesti ilman suurempaa kaavaa, meillä on sille melko hyvä estimaatti, mikä tarkoittaa, että meillä on hyvä käsitys siitä, miten alkuluvut kasvavat, ainakin keskimäärin.
On kuitenkin pidettävä mielessä, että näennäinen tasaisuus on petollista. Läheltä katsottuna, tältä näyttävät kaksi ylintä käyrää:

Kommentteja?
Heuristinen päättely kaksoispriimeistä
Kaksoispriimit ovat pari $p$, $p+2$, jotka molemmat ovat alkulukuja. Esimerkiksi yhdestä yllä olevasta kuvaajasta näemme kaksoisprimit $$ , , , , , , , $$$
ja muita. On arveltu, että niitä on ääretön määrä, mutta vaikka tästä on paljon empiiristä todistusaineistoa, sitä ei ole vielä todistettu.
Vähemmänkin vahvana todisteena on ehkä kaava, joka approksimoi hämmästyttävän hyvin kaksoispriminien $\pi_{2}(x)$ lukumäärää $\le x$. En ole aivan varma tämän kaavan alkuperästä, mutta se esiintyi ensimmäisen kerran G. H. Hardyn ja J. E. Littlewoodin (itsekin kaksoispriimipari) artikkelissa vuodelta 1923. Paperi sisältää useita samankaltaisia kaavoja, jotka kaikki perustuvat samaan menetelmään, jota he olivat käyttäneet monien ongelmien ratkaisemiseen aiemmin. Tämä oli heidän ympyrämenetelmänsä. Heidän $\pi_{2}(x)$-kaavansa johtaminen ei ole lainkaan tiukka, mutta se on hyvin vakuuttava. Andrew Granvillen artikkelin liitteessä on tiivis selostus tästä.
Mutta heti toisen maailmansodan jälkeen lordi Cherwell (Frederick Lindemann) ehdotti alkeellisempaa todennäköisyyteen perustuvaa (eikä edelleenkään järkälemäistä) johdatusta. Tämä johti yhteistyöhön E. M. Wrightin kanssa ja lopulta postuumisti julkaistuun yhteisjulkaisuun. Tämä selitetään Hardyn ja Wrightin tunnetun tekstin kohdassa 22.20. Hieman alkeellisempi versio tästä löytyy myös Granvillen artikkelin liitteestä (kohta 2.5). Seuraan häntä.
Lähtökohtana uskottavalle päättelylle on arviomme $\pi(x)$:lle, niiden alkulukujen lukumäärälle, jotka ovat pienempiä tai yhtä suuria kuin $x$. Johdannon perusajatus on, että alkuluvut ovat suurelta osin satunnaisesti jakautuneita. Tiedämme, että $x$:n läheisyydessä alkulukujen tiheys on noin $1/\log x$. Jos alkuluvut jakautuisivat satunnaisesti, todennäköisyys sille, että kaksi tiettyä lukua lähellä $x$ on alkulukuja, olisi vain paikallisten todennäköisyyksien tulo, joka on $1/\log^{2} x$. Tämä on varmasti epäilyttävää päättelyä, sillä jos $n > 2$, todennäköisyys sille, että sekä $n$ että $n+1$ ovat alkulukuja, on $0$, kun taas se, että $p$ on alkuluku, näyttäisi lisäävän todennäköisyyttä sille, että $p+2$ on. Samanlaisia näkökohtia on otettava huomioon myös $x$:n läheisyydessä olevien muiden pienten alkulukujen mahdollisen jaettavuuden vuoksi.
Tässä tarinassa on yksi yksinkertainen tosiasia. Jos $q$ on mikä tahansa alkuluku, todennäköisyys valita satunnaisesti kokonaisluku, joka ei ole jaollinen $q$:llä, on $1-1/q$. Todennäköisyys valita kaksi sellaista lukua, jotka eivät ole jaollisia $q$:lla, on siis tulo $(1 – 1/q)^{2}$. Oletetaan, että $p$ ja $p+2$ ovat molemmat alkulukuja, jolloin kumpikaan luvuista $p$ ja $p+2$ ei ole jaollinen $q$:llä. Jos $q = 2$, näin tapahtuu 1/2$ kertaa. Jos $q \ne 2$, todennäköisyys sille, että $p \not\equiv 0$ ja $p \not\equiv -2$ modulo $q$ on $(1 – 2/q)$. Kiinalaisen jäännöslausekkeen vuoksi kahdella alkuluvulla jaettavuus on riippumaton tapahtuma. Jos siis $x$ on suuri ja $Q$ suhteellisen pieni, todennäköisyys sille, että jokin $x$:n lähellä oleva lukupari $m$ ja $n$ ei ole minkään alkuluvun kerrannainen $Q$:n rajoissa, on $$$ { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Olkoon $\Gamma_{Q}$ tämän suhde $\prod_{q \le Q}(1 – 2/q)$:een: $$$ \Gamma_{Q} = { { 1\over 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } \over (1 – 2/q) } $$ Meillä on $$ { { 1 – 2/q \over (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} \over (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Standardikriteeri väittää, että tämä tuote konvergoi, jos summa $\sum 1/(q-1)^{2}$ konvergoi. Mutta se konvergoi, koska integraalitesti kertoo, että $\summa 1/n^{2}$ konvergoi. Siksi tämä tulo itse asiassa konvergoi lukuun $\Pi_{\infty}$, kun $Q \rightarrow \infty$. Olkoon $C_{2}$ sen käänteisluku. Granvillen artikkelin kohdassa 2.5 sanotaan, että tässä vaiheessa pitäisi olla intuitiivisesti järkevää, että kaksoisprimäärien $\pi_{2}(x)$ lukumäärä $\pi_{2}(x)$ on likimain $$ \Pi_{2}(x) = C_{2} \int_{2}^{\infty} { dx \over \log^{2} x } \, . $$
Hardyn ja Wrightin tekstissä esitetään huolellisempi analyysi, joka tekee intuitiivisen hyppäyksen hieman selvemmäksi.
J. W. Wrench laski jo kauan sitten vakion arvoksi tässä noin 1 $.3203236316937391414785562422002911155686525 \ldots $. Seuraavassa verrataan eräitä $\pi_{2}(x)$:n ja kaavan arvoja alueella $$: $$ $$ \matrix{ n & 10,000 & 20,000 & 30,000 & 40,000 & 50,000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214.2 & 357.7 & 486.7 & 607.4 & 722.5 \cr } $$ $$ \matrix{ n & 60,000 & 70,000 & 80,000 & 90,000 & 100,000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833.3 & 940.9 & 1045.7 & 1148.2 & 1248.7 \cr } $$
Kommentteja?
Dicksonin arvelu
Kaksoisplussat ovat erikoistapaus jostain paljon yleisemmästä. Voidaan kysyä, onko olemassa ääretön määrä pareja $p$, $p+4$ tai $p$, $p+6$, jotka ovat alkulukuja? Tai $p$, $p+10$? Tapaukseen $p$ ja $p+10$ viittaa varmasti yksi yllä olevista kuvista, joissa tällaiset parit ovat helposti nähtävissä. Entäpä jonkinlaiset kolmoset? Oletetaan, että $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ muodostavat kokonaislukujen joukon. Voimmeko olettaa, että on ääretön määrä joukkoja $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$, jotka kaikki ovat alkulukuja?
On oltava hieman varovainen. Ei ole olemassa alkulukupareja muodossa $p$, $p+1$ (menneisyydessä $p = 2$), koska jommankumman näistä kahdesta luvusta on oltava jaollinen $2$:lla. Vastaavasti yli $p = 3$ ei ole alkukolmosia $p$, $p+2$, $p+4$, koska jommankumman näistä täytyy olla jaollinen 3$:lla.
Tämän viimeisen esimerkin pitäisi olla valaiseva. Luku $p+4$ on jaollinen $3$:lla, jos ja vain jos $p+1$ on jaollinen $3$:lla. Näin ollen $3$ jakaa jonkin luvuista $p$, $p+2$, $p+4$, jos ja vain jos se jakaa luvut $p$, $p+1$, $p+2$. Mutta näin tapahtuu varmasti, koska viimeinen kolmikko kattaa selvästi kaikki luvut modulo $3$.
Yleisesti $p$ sanotaan olevan este joukolle $(a_{i})$, jos $p$ jakaa aina vähintään yhden jokaisesta sarjasta $n+a_{i}$ ($i = 1$, $\ldots$, $k$). Tämä tapahtuu, jos ja vain jos luvut $a_{i} \; {\rm mod} \, p$ täyttävät koko $Z/p$.
Tämä ei voi koskaan tapahtua, jos $p > k$, joten tarkistaaksemme, estääkö jokin $p$ $(a_{i})$, meidän tarvitsee vain tarkistaa, peittävätkö $a_{i}$ $Z/p$ kaikilla $p \le k$. Kutsumme joukkoa $(a_{i})$ sallituksi, jos sillä ei ole mitään alkulukujen esteitä.
Esimerkiksi $(1,3,7,9)$ on sallittu joukko, koska, kuten voit helposti tarkistaa, $2$ ja $3$ eivät ole esteitä. Useita tähän kuvioon sopivia alkusarjoja voidaan nähdä yhdessä yllä olevista kaavioista. Muita esimerkkejä ovat (a) mikä tahansa $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
On olemassa mielivaltaisen suuria sallittuja joukkoja. Itse asiassa:
Teoreema. Jos $a_{1}$ – $a_{k}$ on mikä tahansa joukko erillisiä alkulukuja $> k$, ne muodostavat sallitun joukon.
Miksi näin on? Jos $p$ on mikä tahansa alkuluku, jossa $p> k$, niin olemme jo nähneet, että se ei voi olla este. Mutta jos $p \le k$, niin se ei voi jakaa mitään $a_{i}$:tä, joista yksikään ei voi olla kongruentti $0$ modulo $p$:n kanssa. $a_{i}$ ei siis täytä $Z/p$.
L. E. Dicksonin alunperin esittämän arvelun erikoistapaus on, että jos $(a_{i})$:lle ei ole alkulukujen esteitä, niin silloin on olemassa äärettömän monta alkulukusarjaa, jotka ovat muotoa $(n +a_{i})$.
Mitä on tapahtunut viime aikoina
Tämä ei ole oikea paikka kertoa koko tarinaa, joka on käsitelty perusteellisesti muualla. Suosittelen erityisesti Erica Klarreichin Quanta-artikkelia suositellun selostuksen saamiseksi ja Granvillen esseetä teknisemmän selostuksen saamiseksi. Haluan vain todeta hieman tarkemmin kuin Klarreichin selostuksessa, mikä on tunnetuin uusista tuloksista.
Se on Yitang Zhangin ansiota. Yksinkertaisin toteamus siitä, mitä hän todisti, on, että on olemassa ääretön määrä välejä $[n, n+70,000,000)$, jotka sisältävät vähintään kaksi alkulukua. Tämä on heikompi kuin twin primes conjecture, mutta käsitteellisesti hyvin lähellä sitä. Myöhemmässä työssä (monien matemaatikkojen toimesta) välin kokoa on pienennetty huomattavasti, mutta nykyisillä menetelmillä ei oletettavasti ole mitään keinoa pienentää sitä arvoon $2$.
Kuten Granville selittää, Zhangin ensimmäinen ja luultavasti hänen tärkein tuloksensa on, että on olemassa $k$, jolla on ominaisuus, että jos $a_{1}$, $\ldots$ , $a_{k}$ on sallittu joukko, jossa on $k$ alkioita, niin on olemassa ääretön määrä $n$ siten, että $\{ n +a_{i} \}$ sisältää vähintään kaksi alkulukua. (Klarreichin Quanta-artikkelissa joukkoa kutsutaan ”kammaksi”. Muista, että Dicksonin arvelun mukaan meidän pitäisi voida sanoa, että kaikki $k$ ovat alkulukuja). Itse asiassa Zhang osoitti, että tämä väite pitää paikkansa tietylle $k =3 500 000$:lle, joka kattaa $70 000 000$:n välein. Tähän mennessä kuuluisa seuraus on, että jollekin $m \lt 70 000 000$ on olemassa ääretön määrä alkulukupareja $p$, $p+m$.
Lue lisää
- Lord Cherwell ja E. M. Wright, ”The frequency of prime patterns”, The Quarterly Journal of Mathematics 11 (1960).
Ne, jotka tietävät jotakin lordi Cherwellin, joka muuten tunnetaan nimellä Frederick Lindemann, elämästä, yllättyvät suuresti kuullessaan hänen panoksestaan lukuteoriaan. Wikipedian elämäkerta ei osoita riittävästi kaikkia syitä hänen huonoon maineeseensa Churchillin tieteellisenä pääneuvonantajana toisen maailmansodan aikana.
- L. E. Dickson, ”A new extension of Dirichlet’s theorem on prime numbers”, Matematiikan sanansaattaja 33.
Vrt. myös Wikipedian merkintä Dicksonin arvelusta.
- Andrew Granville, ”Primes in intervals of bounded length”. Saatavilla hänen kotisivultaan.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Luku 2.5 sisältää ideaalisen johdannon mahdollisesta kaavasta $\pi(x)$:lle.
- G. H. Hardy ja J. E. Littlewood, ”Some problems of ’Partitio numerorum’ III: on the expression of a number as a sum of primes”, Acta Mathematica 44 (1923).
- G. H. Hardy ja E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, ”Together and alone, closing the prime gap”, Quanta 19. marraskuuta 2013.
- B. Riemann, ”On the number of prime numbers less than a given amount”. David Wilkinsin englanninkielinen käännös tästä klassikosta on saatavilla Wikipediassa olevasta linkistä.
Tässä hahmotellaan muun muassa likimääräisen kaavan $\pi(x)$ johtaminen.
- J. W. Wrench, ”Evaluation of Artin’s constant and the twin-prime constant”, Mathematics of Computation 76 (1961).
Varhainen laskutoimitus $C_{2}$:lle.
- Luettelot alkuluvuista aina $1,000,000,000,000,000,000$ asti
- Luettelo 20,000 ensimmäisestä kaksoisalkuluvusta.
 Bill Casselman
Bill Casselman
Britannian Kolumbian yliopisto, Vancouver, Kanada
Sähköposti Bill Casselman
.