Säätöjärjestelmien suorituskyvyn parantamiseen käytetään erityyppisiä säätimiä. Tässä luvussa käsitellään perussäätimiä, kuten proportionaali-, derivaatta- ja integraalisäätimiä.
Suhteellinen säädin
Suhteellinen säädin tuottaa ulostulon, joka on verrannollinen virhesignaaliin.
$$u(t) \propto e(t) $$
$$$\oikea nuoli u(t)=K_P e(t)$$
Sovelletaan Laplace-muunnosta molemmille puolille –
$$U(s)=K_P E(s)$$
$$$\frac{U(s)}{E(s)}=K_P$$
Siten, proportionaalisäätimen siirtofunktio on $K_P$.
Jossa,
U(s) on toimilaitesignaalin u(t)
E(s) on virhesignaalin e(t)
KP on suhteellisuusvakio
Yksikäsitteisen negatiivisesti takaisinkytketyn suljetun silmukan säätöjärjestelmän lohkokaavio yhdessä proportionaalisäätimen kanssa on esitetty seuraavassa kuvassa.
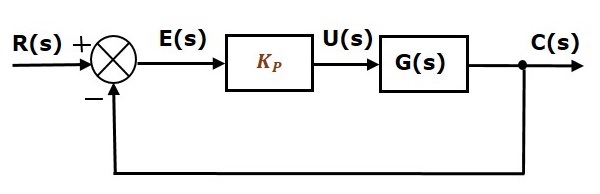
Suhteellista säädintä käytetään muuttamaan transienttista vastetta tarpeen mukaan.
Derivaatiosäädin
Derivaatiosäädin tuottaa ulostulon, joka on virhesignaalin derivaatta.
$$u(t)=K_D \frac{\text{d}e(t)}{{\text{d}t}t}$$$$
Sovelletaan molemmille puolille Laplace-muunnosta.
$$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$$
Siten derivaattasäätimen siirtofunktio on $K_D s$.
Jossa $K_D$ on derivaattavakio.
Yksikäsitteisen negatiivisesti takaisinkytketyn suljetun silmukan säätöjärjestelmän lohkokaavio yhdessä derivaatiosäätimen kanssa on esitetty seuraavassa kuvassa.
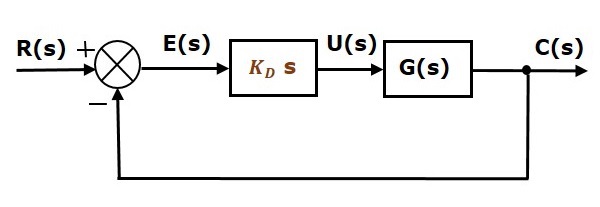
Derivaatiosäädintä käytetään tekemään epästabiilista säätöjärjestelmästä stabiili.
Integraalisäädin
Integraalisäädin tuottaa ulostulon, joka on virhesignaalin integraali.
$$u(t)=K_I \int e(t) dt$$
Sovelletaan Laplace-muunnosta molemmille puolille –
$$U(s)=\frac{K_I E(s)}{s}$$
$$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$$$
Selvä, integraalisäätimen siirtofunktio on $\frac{K_I}{s}$.
Jossa $K_I$ on integraalivakio.
Yksikäsitteisen negatiivisesti takaisinkytketyn suljetun silmukan säätöjärjestelmän lohkokaavio yhdessä integraalisäätimen kanssa on esitetty seuraavassa kuvassa.
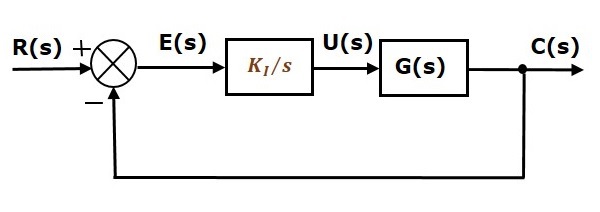
Integraalisäädintä käytetään pienentämään pysyvän tilan virhettä.
Keskustellaan nyt perussäätimien yhdistelmästä.
Proportionaalinen derivaattasäädin (PD-säädin)
Suhteellinen derivaattasäädin tuottaa ulostulon, joka on proportionaalisen ja derivaattasäätimen ulostulojen yhdistelmä.
$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$$$
Sovelletaan Laplace-muunnosta molemmille puolille – –
$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$$
Siten, proportionaalisen derivaatiosäätimen siirtofunktio on $K_P + K_D s$$.
Yksikäsitteisen negatiivisesti takaisinkytketyn suljetun silmukan säätöjärjestelmän lohkokaavio yhdessä proportionaalisen derivaatiosäätimen kanssa on esitetty seuraavassa kuvassa.
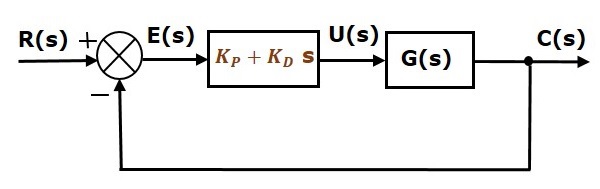
Suhteellista derivaattasäädintä käytetään parantamaan säätöjärjestelmän stabiilisuutta vaikuttamatta vakiotilavirheeseen.
Suhteellinen integraali (PI) säädin
Suhteellinen integraali säädin tuottaa ulostulon, joka on yhdistelmä proportionaalisen ja integraali säätimien ulostuloista.
$$u(t)=K_P e(t)+K_I \int e(t) dt$$
Sovelletaan Laplace-muunnosta molemmille puolille –
$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$$
Siten, proportionaalisen integraalisäätimen siirtofunktio on $K_P + \frac{K_I} {s}$.
Yksikäsitteisen negatiivisesti takaisinkytketyn suljetun silmukan säätöjärjestelmän lohkokaavio yhdessä proportionaalisen integraalisäätimen kanssa on esitetty seuraavassa kuvassa.
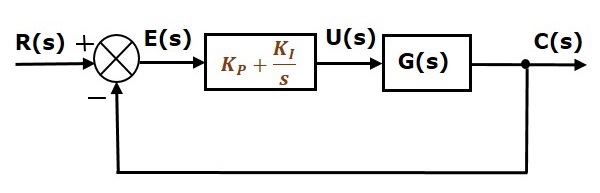
Suhteellista integraalisäädintä käytetään pienentämään pysyvän tilan virhettä vaikuttamatta säätöjärjestelmän stabiilisuuteen.
Proportionaalinen integraalinen derivaattorisäädin (PID-säädin, PID-säädin)
Suhteellinen integraalinen derivaattorisäädin (PID-säädin) tuottaa ulostulon, joka on proportionaalisen-, integraali-, ja derivaattorisäätimissä olevien lähtöarvojen tuloilmoitusten tuloilmoitusten muodostama yhdistelmä.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$$
Sovelletaan Laplace-muunnosta molemmille puolille –
$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$$
Siten, proportionaalisen integraali-derivaatiosäätimen siirtofunktio on $K_P + \frac{K_I} {s} + K_D s$$.
Yksikäsitteisen negatiivisesti takaisinkytketyn suljetun silmukan säätöjärjestelmän lohkokaavio yhdessä proportionaalisen integraalijohdannaisohjaimen kanssa on esitetty seuraavassa kuvassa.
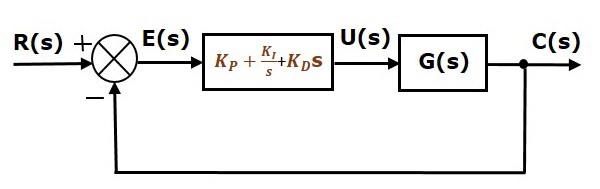
Suhteellista integraalijohdannaisohjainta käytetään parantamaan säätöjärjestelmän stabiilisuutta ja pienentämään stabiilin tilan virhettä.