Puoli yhteenlaskija ja täysi yhteenlaskija piiri
Puoli yhteenlaskija ja täysi yhteenlaskija piirit selitetään niiden totuustaulukot tässä artikkelissa. Täyden yhteenlaskijan suunnittelu käyttäen puoli yhteenlaskijapiiriä näytetään myös. Yksibittinen Full Adder -piiri ja monibittinen yhteenlasku Full Adderin avulla näytetään myös.
Ennen tämän aiheen käsittelyä on erittäin tärkeää tietää Boolen logiikasta ja loogisista porteista.
KATSO : BOOLINEN LOGIIKKA
KATSO : LOGIIKKAPORTIT
KATSO : FLIP FLOPS
Mikä on yhteenlaskija?
Lisäyslaskija on eräänlainen laskutoimilaite, jota käytetään kahden binääriluvun lisäämiseen. Kun sanon, laskin, en tarkoita sellaista, jossa on painikkeet, tämä on piiri, joka voidaan integroida monien muiden piirien kanssa monenlaisia sovelluksia varten. Yhteenlaskijoita on kahdenlaisia;
- Puoliyhteenlaskija
- Täysi yhteenlaskija
Puoliyhteenlaskija
Puoliyhteenlaskijan avulla voimme suunnitella piirejä, jotka kykenevät suorittamaan yksinkertaisen yhteenlaskun loogisten porttien avulla.
Katsotaan ensin yksittäisten bittien yhteenlasku.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Nämä ovat vähiten mahdollisia yksittäisten bittien yhdistelmiä. Mutta 1+1:n tulos on 10. Vaikka tämä ongelma voidaan ratkaista EXOR-portin avulla, jos välität tuloksesta, summatulos on kirjoitettava uudelleen 2-bittiseksi tulokseksi.
Siten yllä olevat yhtälöt voidaan kirjoittaa seuraavasti
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Tässä ulostulosta ’1’ ’10’ tulee carry-out. Tulos on esitetty alla olevassa totuustaulukossa. ’SUM’ on normaali ulostulo ja ’CARRY’ on ulostulo.
INPUTS OUTPUTS
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
Yhtälöstä, on selvää, että tämä 1-bittinen yhteenlaskija voidaan helposti toteuttaa EXOR-portin avulla ulostuloa ’SUM’ varten ja AND-portin avulla siirtoa varten. Katso alla olevaa toteutusta.
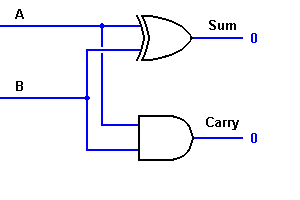
Kompleksisessa yhteenlaskussa voi olla tapauksia, joissa on laskettava yhteen kaksi 8-bittistä tavua. Tämä onnistuu vain täyden yhteenlaskurin logiikan avulla.
Täydellinen yhteenlaskija
Tämä yhteenlaskurityyppi on hieman vaikeampi toteuttaa kuin puolikas yhteenlaskija. Tärkein ero puoliyhtälön ja täysyhtälön välillä on se, että täysyhtälössä on kolme sisääntuloa ja kaksi ulostuloa. Kaksi ensimmäistä sisääntuloa ovat A ja B ja kolmas sisääntulo on sisääntulon carry, jota kutsutaan nimellä CIN. Kun täysi yhteenlaskurilogiikka on suunniteltu, pystymme liittämään kahdeksan tällaista yhteenlaskuria yhteen ja luomaan tavun laajuisen yhteenlaskurin ja kaskadoimaan carry-bitin yhdestä yhteenlaskurista seuraavaan.
Lähdön carry-bittiä merkitään COUT:lla ja normaalia ulostuloa merkitään S:llä. Katsokaa totuustaulukkoa.
SYÖTTEET LÄHDÖT
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1 1
Yllä olevasta totuudesta-taulukosta, voidaan toteuttaa täydellinen yhteenlaskulogiikka. Näemme, että ulostulo S on EXOR tulon A ja puolittaisen summaajan SUM-ulostulon välillä, jossa on tulot B ja CIN. Meidän on myös huomioitava, että COUT on tosi vain, jos jompikumpi kahdesta tulosta kolmesta on HIGH.
Siten voimme toteuttaa täyden yhteenlaskijapiirin kahden puoliyhdistäjäpiirin avulla. Ensimmäistä puolikasta summaajaa käytetään lisäämään A ja B osittaisen summan tuottamiseksi. Toista puolikkaan yhteenlaskijan logiikkaa voidaan käyttää lisäämään CIN ensimmäisen puolikkaan yhteenlaskijan tuottamaan summaan lopullisen S-ulostulon saamiseksi. Jos jokin puolikkaan yhteenlaskijan logiikasta tuottaa siirron, ulostuloon tulee siirto. Näin ollen COUT on puolittaisen yhteenlaskijan Carry-ulostulojen OR-funktio. Tutustu alla esitettyyn täyden yhteenlaskurin piirin toteutukseen.
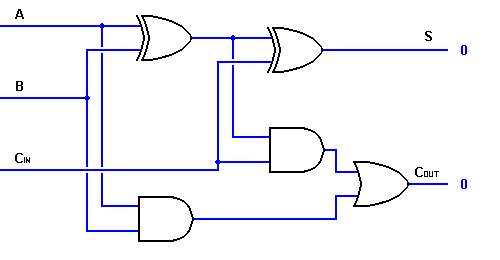
Vaikka edellä esitetyllä täyden yhteenlaskurin logiikalla on mahdollista toteuttaa suurempia logiikkakaavioita, käytetään operaation esittämiseen useimmiten yksinkertaisempaa symbolia. Alla on esitetty yksinkertaisempi kaavamainen esitys yhden bitin täydestä yhteenlaskijasta.
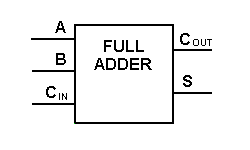
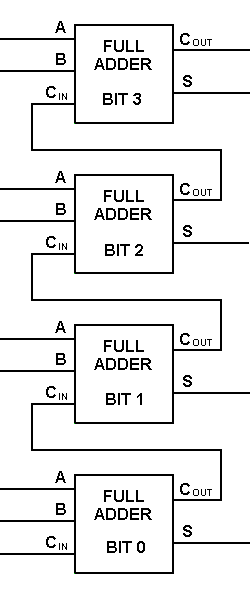
Tämmöisellä symbolilla voimme laskea kaksi bittiä yhteen ottamalla siirron seuraavaksi alemmasta suuruusluokasta ja lähettämällä siirron seuraavaksi ylempään suuruusluokkaan. Tietokoneessa monibittistä operaatiota varten jokainen bitti on esitettävä täydellä yhteenlaskijalla, ja ne on lisättävä samanaikaisesti. Kahden 8-bittisen luvun yhteenlaskuun tarvitaan siis 8 täyttä yhteenlaskijaa, jotka voidaan muodostaa kaskadoimalla kaksi 4-bittistä lohkoa. Kahden 4-bittisen luvun yhteenlasku on esitetty alla.