Aloitetaan tarkastelemalla arvojen jakamista eksponenttien avulla.
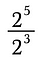
Muistetaan, että eksponentit edustavat toistuvaa kertomista. Voimme siis kirjoittaa yllä olevan lausekkeen uudelleen seuraavasti:
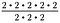
Sen vuoksi, että 2/2 = 1, peruutetaan kolme sarjaa 2/2. Jäljelle jää 2 – 2 eli 2 neliössä.
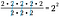
Voidaan tietysti käyttää oikotietä ja vähentää alhaalla olevien 2:iden määrä ylhäällä olevien 2:iden määrästä. Koska näitä suureita edustavat niiden eksponentit, meidän tarvitsee vain kirjoittaa yhteinen perusta ja eksponenttien arvojen erotus potenssina.
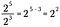
Jos yleistämme tätä sääntöä, saamme seuraavan, jossa n edustaa nollasta poikkeavaa reaalilukua ja x ja y ovat myös reaalilukuja.
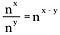
Nollapotenssin tutkiminen
Tästä on helppo johtaa selitys sille, miksi mikä tahansa nollasta poikkeava luku, joka on nostettu nollapotenssiin, on yhtä kuin 1. Tarkastellaan taas konkreettista esimerkkiä.
Tiedämme, että mikä tahansa nollasta poikkeava luku jaettuna itsellään on yhtä kuin 1. Voin siis kirjoittaa seuraavasti:
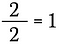
Tämä on sama kuin kirjoittaisi:
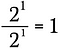
Hyödynnän nyt edellä mainittua eksponenttisääntöä kirjoittaakseni tämän yhtälön vasemman puolen uudelleen.
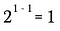
Tämä vastaa tietenkin:
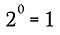
Voidaan käyttää samaa prosessia kuin tässä esimerkissä sekä edellä esitettyä yleistettyä sääntöä osoittaaksemme, että minkä tahansa nollasta riippumattoman reaaliluvun, joka korotetaan nollan potenssiin, on tuloksena oltava 1.
Mikä on nollan potenssiin nolla?
Tässä kohtaa asiat muuttuvat hankaliksi. Yllä oleva menetelmä katkeaa, koska nollalla jakaminen ei tietenkään ole sallittua. Tutkitaanpa miksi.
Aloitetaan tarkastelemalla tavallista jakamista nollalla VIRHE.
Miten olisi 2÷0? Katsotaan, miksi tätä ei voi tehdä.
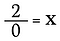
Jaottaminen on oikeastaan vain kertolaskun muoto, joten mitä tapahtuu, jos kirjoitan yllä olevan yhtälön uudelleen seuraavasti:
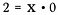
Mikä arvo voisi mahdollisesti tyydyttää tämän yhtälön x:lle?
Ei ole mitään arvoa! Mikä tahansa luku kertaa nolla johtaa nollaan, se ei voi koskaan olla yhtä suuri kuin 2. Siksi sanomme, että jako nollalla on määrittelemätön. Mahdollista ratkaisua ei ole.
Katsotaan nyt 0÷0.
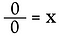
Kirjoitetaan taas uudelleen kertolaskuongelmaksi.
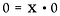
Tässä kohtaamme hyvin erilaisen tilanteen. Ratkaisu x:lle voisi olla MIKÄ tahansa reaaliluku! Ei ole mitään keinoa määrittää, mikä x on. Näin ollen 0/0 katsotaan epämääräiseksi*, ei määrittelemättömäksi.
Jos yritämme käyttää edellä mainittua menetelmää nollan ollessa lähtökohtana määrittääksemme, mitä nolla nollan potenssiin olisi, pysähdymme välittömästi emmekä voi jatkaa, koska tiedämme, että 0÷0 ≠ 1, mutta se on epämääräinen.
Mitä siis vastaa nolla nollan potenssiin?
Tästä keskustellaan paljon. Joidenkin mielestä se pitäisi määritellä 1:ksi, kun taas toisten mielestä se on 0, ja joidenkin mielestä se on määrittelemätön. Kummallekin on hyviä matemaattisia perusteluja, ja ehkäpä sitä pidetäänkin oikeimmin määrittelemättömänä.
Tästä huolimatta matemaattinen yhteisö kannattaa nollan määrittelemistä nollan potenssiin 1:ksi, ainakin useimpiin tarkoituksiin.
Hyödyllinen eksponenttien määritelmä harrastelijamatemaatikolle on ehkä seuraava: