
Älä koskaan jaa nollalla. Meille kaikille opetettiin tämä koulussa, ja useimmissa arkipäivän tilanteissa se on hyvä neuvo. Harvoin on järkevää jakaa mitään nollalla, ja jos yrität pyytää Siriä tekemään sen, hän sanoo, ettei sinulla ole ystäviä.
Mutta miksi juuri nollalla jakaminen on niin huono idea? Ja onko tapauksia, joissa nollalla jakaminen voi olla hyvä asia? Jos et kiinnittänyt huomiota lukiossa, nopea kertauskerta voi avata silmäsi yhdelle matematiikan monista ihmeistä.
Nollalla jakaminen ei ole järkevää, koska aritmetiikassa nollalla jakaminen voidaan tulkita myös nollalla kertomisena. 3/0=X on sama yhtälö kuin 0*X=3. Ilmeisesti X:n tilalle ei voi liittää mitään lukua, joka saisi yhtälön toimimaan.
Samankaltainen tilanne syntyy, jos yrität jakaa nollan itsellään. 0/0=X voidaan kirjoittaa uudelleen muotoon 0*X=0, ja ongelma tässä on se, että jokainen luku toimii. X voi olla mikä tahansa, joten tämä yhtälö ei ole kovin hyödyllinen.
Mutta on joitakin tapauksia, joissa jakaminen nollalla todella toimii, ja on itse asiassa välttämätöntä ongelman ratkaisemiseksi. Tämä oli Newtonin oivallus, kun hän keksi laskutoimituksen.
Esimerkiksi, sinulla on käyrä ja yrität löytää alla olevan käyrän kaltevuuden tietyssä pisteessä. Tämä on sama kuin yrittäisit löytää sellaisen suoran kaltevuuden, joka koskettaa käyrää vain kyseisessä pisteessä, jota kutsutaan tangenttisuoraksi. Monissa tapauksissa tuon kaltevuuden löytäminen pelkän algebran avulla on mahdotonta.
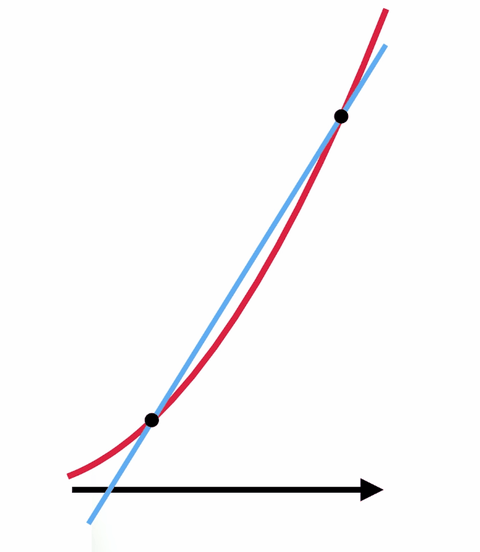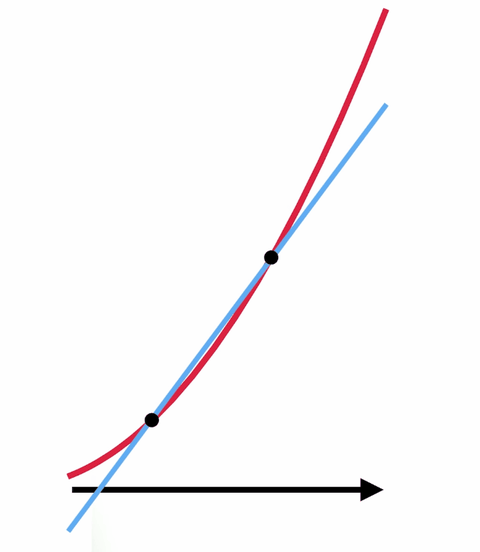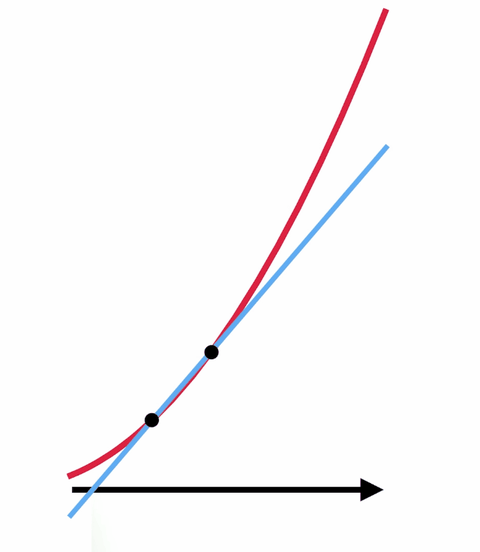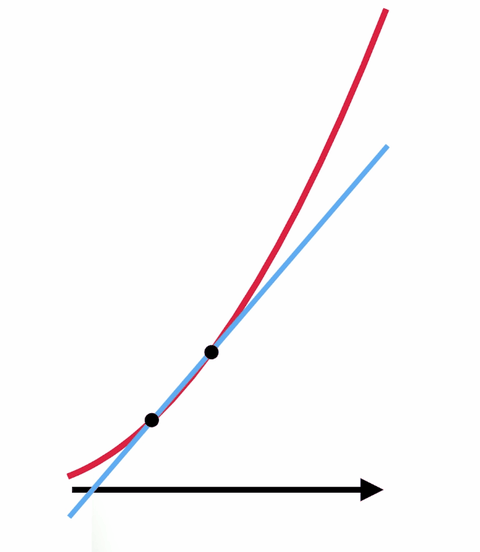

Mutta on olemassa temppu, jossa käytetään laskutoimitusta ja nollalla jakamisen taikaa. Tangenttisuoran etsimisen sijaan on paljon helpompaa löytää sellaisen suoran kaltevuus, joka koskettaa käyrää kahdessa pisteessä. Jos siirrät näitä kahta pistettä yhä lähemmäs toisiaan, saat viivan, joka on lähellä haluamaasi viivaa.
Jos siirrät näitä kahta pistettä niin, että ne ovat päällekkäin – niin että niitä on käytännössä vain yksi – saat alkuperäisen haluamasi tangenttisuoran, mutta tällä kertaa voit löytää kaltevuuden. Jaat periaatteessa nollan itsellään ja saat vastauksen.
Temppu nollalla jakamisessa on periaatteessa se, että luodaan jokin ylimääräinen konteksti. Alkuperäinen ongelma 0/0:n kanssa on se, että jokainen luku voisi potentiaalisesti olla vastaus, joten ottamalla käyttöön joitakin rajoittavia tekijöitä voidaan rajata mahdollisia vastauksia.
Ja kun pystyt jakamaan nollalla, avautuu aivan uusi matematiikan maailma. Nollilla ja äärettömyyksillä ja kaikenlaisilla mahdottomilla yhtälöillä leikkimisestä tulee arkipäivää. Opettele jakamaan nollalla, eikä matematiikka ole enää koskaan entisensä.