Matematiikan mallintaminen

by admin Leave Comment

Oppimistavoitteet

  • Tutustuminen paloittain lineaarisiin funktioihin
    • Määrittele paloittain lineaariset funktiot. funktio
    • Arvioi kappalemittainen funktio
    • Kirjoita kappalemittainen funktio annetun sovelluksen perusteella
  • Graafi kappalemittaiset funktiot
    • Anna kappalemittainen-määritelty funktio, luonnostele kuvaaja
    • Kirjoita paloittain määritellyn funktion alue ja vaihteluväli annetun kuvaajan perusteella

Jotkut funktiot ovat paloittain. Tässä osiossa opimme, miten määritellä ja graafisoida funktioita, jotka ovat pohjimmiltaan diskreettien kappaleiden kokoelmia. Esimerkkejä näin määritellyistä funktioista ovat esimerkiksi auton profiilin suunnittelu, matkapuhelinliittymän laskeminen ja tuloveroprosenttien laskeminen. Esimerkiksi veroprosenttisi riippuu tuloistasi ja on sama erilaisille tuloille, kuten alla olevasta taulukosta käy ilmi:

Marginaaliveroprosentti Yksin veronalaiset tulot Married Filing Jointly or Qualified Widow(er) Taxable Verotettava tulo Vanhemmat, jotka jättävät hakemuksensa erikseen Verotettava tulo Kotitalouden päämies Verotettava tulo
10% $0 – $9,275 $0 – $18,550 $0 – $9,275 $0 – $13,250
15% $9,276 – $37,650 $18,551 – $75,300 $9,276 – $37,650 $13,251 – $50,400
25% $37,651 – $91,150 $75,301 – $151,900 $37,651 – $75,950 $50,401 – $130,150
28% $91,151 – $190,150 $151,901 – $231,450 $75,951 – $115,725 $130,151 – $210,800
33% $190,151 – $413,350 $231,451 – $413,350 $115,726 – $206,675 $210,801 – $413,350
35% $413,351 – $415,050 $413,351 – $466,950 $206,676 – $233,475 $413,351 – $441,000
39.6% $415,051+ $466,951+ $233,476+ $441,001+

Paloittainen funktio (piecewise function) on funktio, jossa tuloksen määrittelyyn käytetään useampaa kuin yhtä kaavaa toimialueen eri osien yli.

Käytämme kappaleittaisia funktioita kuvaamaan tilanteita, joissa sääntö tai suhde muuttuu, kun tuloarvo ylittää tietyt ”rajat”. Esimerkiksi liike-elämässä törmäämme usein tilanteisiin, joissa tietyn tuotteen kappalekohtaista hintaa alennetaan, kun tilattu määrä ylittää tietyn arvon. Veroluokat ovat toinen reaalimaailman esimerkki kappaleittaisista funktioista. Tarkastellaan esimerkiksi yksinkertaista verojärjestelmää, jossa tuloja 10 000 dollariin asti verotetaan 10 prosentin verokannalla ja kaikkia muita tuloja 20 prosentin verokannalla. Kokonaistulon S vero olisi 0,1S, jos S\le 10 000 dollaria, ja 1000 + 0,2 (S – 10 000 dollaria), jos S> 10 000 dollaria.

Paloittaisfunktio

Paloittaisfunktio on funktio, jossa tuloksen määrittelyyn käytetään useampaa kuin yhtä kaavaa. Jokaisella kaavalla on oma alueensa, ja funktion alue on kaikkien näiden pienempien alueiden unioni. Merkitsemme tämän ajatuksen näin:

f\left(x\right)=\begin{cases}\text{kaava 1 jos x on toimialueella 1}\\\ \text{kaava 2 jos x on toimialueella 2}\\\ \text{kaava 3 jos x on toimialueella 3}\end{cases}

Kappalemääräisessä notaatiossa absoluuttisen arvon funktio on

|x|=\begin{cases}x\text{ if }x\ge 0\\\\ -x\text{ if }x<0\end{cases}

Kappalemääräisesti määritellyn funktion arviointi

Ensimmäisessä esimerkissä näytetään, miten arvioidaan kappalemääräisesti määritelty funktio. Huomaa, kuinka tärkeää on kiinnittää huomiota toimialueeseen, jotta voidaan määrittää, mitä lauseketta käytetään syötteen arviointiin.

Esimerkki

Annetaan funktio

f(x)=\begin{cases}7x+3\text{ if }x<0\\\7x+6\text{ if }x\ge{0}\end{cases},

arvioi:

  1. f (-1)
  2. f (0)
  3. f (2)
Näytä vastaus

1.f(x) määritellään 7x+3:ksi, kun x=-1\text{ koska }-1<0.

Arvioi: f(-1)=7(-1)+3=-7+3=-4

2. f(x) määritellään 7x+6:ksi, kun x=0\text{ becuase }0\ge{0}.

Arvioi: f(0)=7(0)+6=0+6=6

3. f(x) määritellään 7x+6:ksi, kun x=2\text{ becuase }2\ge{0}.

Arvioi: f(2)=7(2)+6=14+6=20

Seuraavalla videolla näytetään, miten arvioidaan useita arvoja annettuna kappalemaisesti määritetty funktio.

Seuraavassa esimerkissä näytämme, miten arvioidaan funktio, joka mallintaa puhelinyhtiön tiedonsiirron kustannuksia.

Esimerkki

Kännykkäyhtiö käyttää alla olevaa funktiota määrittääkseen g gigatavun tiedonsiirron kustannuksen, C, dollareina.

C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Erittäkää kustannus, joka syntyy, kun käytetään 1.5 gigatavua dataa ja kustannukset, jotka aiheutuvat 4 gigatavun datan käyttämisestä.

Näytä vastaus

Löytääksemme kustannukset, jotka aiheutuvat 1,5 gigatavun datan käyttämisestä, C(1.5), katsomme ensin, mihin osaan toimialuetta syötteemme kuuluu. Koska 1,5 on pienempi kuin 2, käytämme ensimmäistä kaavaa.

C(1,5) = 25 dollaria

Löytääksemme 4 gigatavun datan käytön kustannukset, C(4), näemme, että syötteemme 4 on suurempi kuin 2, joten käytämme toista kaavaa.

C(4)=10(4)+5=45

Ratkaisun analysointi

Funktio on esitetty alla olevassa kuvaajassa. Näemme, missä kohtaa funktio muuttuu vakiosta suoraksi, jolla on positiivinen kaltevuus kohdassa g=2. Piirretään eri kaavojen kuvaajat yhteisille akseleille ja varmistetaan, että kutakin kaavaa sovelletaan oikeaan alueeseensa.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Kirjoita paloittain määritelty funktio

Viimeisessä esimerkissä näytämme, miten kirjoitetaan paloittain määritelty funktio, joka mallintaa opastetun museokierroksen hintaa.

Esimerkki

Museo perii opastetusta kierroksesta 1-9 hengen ryhmältä 5 dollaria per henkilö tai kiinteän 50 dollarin maksun 10 tai useamman hengen ryhmältä. Kirjoita funktio, joka liittää henkilömäärän n hintaan C.

Näytä vastaus

Tarvitaan kaksi eri kaavaa. Jos n:n arvo on alle 10, C=5n. N:n arvoille, jotka ovat 10 tai suuremmat, C=50.

C(n)=\begin{cases}{5n}\text{ if{0}<{n}<{10}\\\ 50\text{ if{n}\ge 10\end{cases}

Ratkaisun analyysi

Funktio on esitetty kuvassa 21. Kuvaaja on diagonaaliviiva n=0:sta n=10:een ja sen jälkeen vakio. Tässä esimerkissä molemmat kaavat ovat yhtä mieltä kohtaamispisteessä, jossa n=10, mutta kaikilla kappaleittain määritellyillä funktioilla ei ole tätä ominaisuutta.

Seuraavalla videolla näytetään esimerkki kappaleittain määritellyn funktion kirjoittamisesta annetun skenaarion perusteella.

Kirjoita kappaleittain määritellyn funktion kaava ja tunnista kunkin intervallin alue.

  1. Tunnista ne intervallit, joihin sovelletaan eri sääntöjä.
  2. Määritä kaavat, jotka kuvaavat, miten lasketaan ulostulo syötteestä kullakin intervallilla.
  3. Käytä hakasulkeita ja if-lausekkeita kirjoittaaksesi funktion.

Graafita kappalemittaisia funktioita

Tässä osassa piirretään kappalemittaisia funktioita. Alla piirretty funktio edustaa tietyn matkapuhelinyhtiön tiedonsiirtokustannuksia. Näemme, missä kohtaa funktio muuttuu vakiosta suoraksi, jolla on positiivinen kaltevuus kohdassa g=2. Kun piirrämme kappaleittain eteneviä funktioita, on tärkeää varmistaa, että kutakin kaavaa sovelletaan oikeaan alueeseensa.C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}

Tässä tapauksessa lähtöarvo on 25 mille tahansa syötteelle välillä 0-2. Jos arvot ovat yhtä suuret tai suuremmat kuin 2, tulokseksi määritetään 10g+5.

Ajattele kuvaaja paloittain etenevälle funktiolle.

  1. Merkitse x-akselille intervallien määrittelemät rajat kullakin toimialueen osalla.
  2. Kunkin toimialueen osalla tee kuvaaja kyseisellä intervalliosalla käyttäen vastaavaa yhtälöä, joka koskee kyseistä osaa. Älä kuvaajaa kahta funktiota yhden intervallin yli, koska se rikkoisi funktion kriteerejä.

Esimerkki

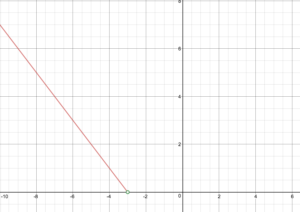
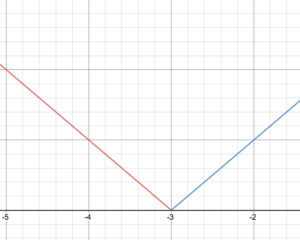
Skeemaile funktion kuvaaja.

Voidaan antaa kappalemääräinen määritelmä f(x)=\begin{cases}-x – 3 \text{ if }x < -3 \\ \ x + 3 \text{ if }. x \ge -3\end{cases}
Piirrä f:n kuvaaja.
Merkitse funktion alue ja vaihteluväli.

Näytä vastaus

Piirrä ensin suora f(x) = -x-3 pyyhkimällä pois se osa, jossa x on suurempi kuin -3. Aseta avoin ympyrä pisteeseen (-3,0).

Sijoita nyt kuvaajaan suora f(x) = x+3 alkaen pisteestä (-3,0). Huomaa, että tässä osassa kuvaajaa piste (-3,0) sisältyy, joten voit poistaa avoimen ympyrän.

Kahden kuvaajan kohtaavat pisteessä (-3,0)

Tämän funktion toimialue on kaikki reaaliluvut, koska piste (-3,0)ei sisälly f(x) = -x-3:n päätepisteeseen, mutta se sisältyy f(x) = x+3:n päätepisteeseen.

Tämän funktion alue alkaa pisteestä f(x)=0, sisältää 0 ja ulottuu äärettömään, joten kirjoittaisimme tämän muotoon x\ge0

Seuraavassa esimerkissä kuvaamme kappalemääräisesti määriteltyä funktiota, joka mallintaa nettisarjakuvien vähittäismyyjän toimituskustannuksia.

Esimerkki

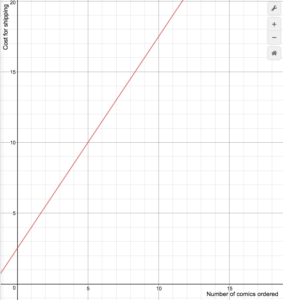
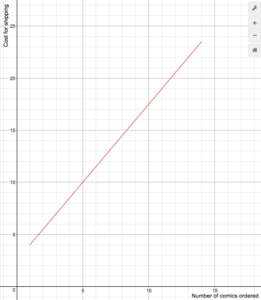
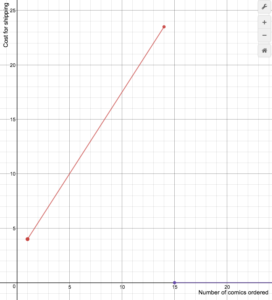
Online-sarjakuvien vähittäismyyjä veloittaa toimituskulut seuraavan kaavan mukaan

S(n)=\begin{cases}1.5n+2.5\text{ if }1\le{n}\le14\\\0\text{ if }n\ge15\end{cases}

Piirrä kustannusfunktion kuvaaja.

Näytä vastaus

Piirretään ensin suora S(n)=1.5n+2.5. Voimme käyttää muunnoksia: tämä on identiteetin pystysuora venytys kertoimella 1,5 ja pystysuora siirtymä kertoimella 2,5.

S(n)=1,5n+2.5

Nyt voimme eliminoida ne kuvaajan osat, jotka eivät ole toimialueella perustuen 1\le{n}\le14

S(n) = 1.5n+2.5, sillä 1<=n<=14

Viimeiseksi lisätään vakiofunktio S(n)=0 syötteille, jotka ovat suuremmat tai yhtä suuret kuin 15. Aseta suljettuja pisteitä kuvaajan päihin osoittamaan päätepisteiden sisällyttämistä.

Seuraavalla videolla näytetään, miten kuvaajaa voidaan piirtää kappalemääräisesti määritellystä funktiosta, joka on lineaarinen molemmilla osa-alueilla.

Yhteenveto

  • Kappalemittainen funktio on funktio, jossa käytetään useampaa kuin yhtä kaavaa tulon määrittelyyn toimialueen eri osien yli.
  • Kappalemittaisen funktion arviointi tarkoittaa, että sinun on kiinnitettävä tarkkaa huomiota oikeaan lausekkeeseen, jota käytetään annetulle syötteelle

Kappalemittaisten funktioiden kuvaajaa varten sinun on ensin selvitettävä, missä kohtaa toimialuetta alue jakautuu. Graafioi funktiot toimialueella käyttäen apuvälineitä, kuten pisteiden piirtämistä tai muunnoksia. Huolehdi siitä, että käytät avoimia tai suljettuja ympyröitä kunkin toimialueen päätepisteissä sen mukaan, onko päätepiste mukana.

Vastaa

Sähköpostiosoitettasi ei julkaista.