Kvadraattisen yhtälön 101 käyttötapaa

Matemaattinen yhtälö ei usein pääse valtakunnalliseen lehdistöön, vielä harvemmin suosittuun radioon, tai mikä hämmästyttävintä, Yhdistyneen kuningaskunnan parlamentin keskusteluun. Vuonna 2003 vanha kunnon kvadraattinen yhtälö, jonka me kaikki opimme koulussa, oli kuitenkin kaikkea tätä.

Mistä aloitamme

Kaikki alkoi Kansallisen opettajien liiton kokouksessa. Kvadraattista yhtälöä pidettiin kansakunnan edessä korkealla esimerkkinä siitä julmasta kidutuksesta, jota matemaatikot kohdistivat pahaa-aavistamattomiin koululaisparoihin. Syytöksestä innostuneena kvadraattinen yhtälö otti pääroolin parhaaseen katseluaikaan radiossa, jossa sitä kuulusteli pelottava haastattelija, joka oli tottuneempi haastateltavaksi pääministerille. (Lontoon) Times käytti Leader-palstallaan, joka on yleensä varattu nykymaailman moraalista (tai muusta) terveydestä käytäville painokkaille keskusteluille, tilaa julistaakseen, että kvadraattinen yhtälö oli hyödytön, matematiikka oli hyödytöntä ja että kukaan ei muutenkaan halunnut opiskella matematiikkaa, joten miksi vaivautua. Koska oltiin huolissaan siitä, etteivät kvadraattisen yhtälön vaaralliset myönnytykset jäisi kyseenalaistamatta, yhtälön elintärkeästä merkityksestä Yhdistyneen kuningaskunnan selviytymiselle keskusteltiin Yhdistyneen kuningaskunnan parlamentin alahuoneessa (myönteinen kanta otettiin, kuten ehkä iloksenne tiedätte).

Mihin tämä kaikki päättyisi? Oliko kvadraattinen yhtälö todella kuollut? Välittikö kukaan siitä? Ovatko matemaatikot todella pahoja hirviöitä, jotka haluavat vain aiheuttaa kvadraattisia yhtälöitä nuoremmalle sukupolvelle keinona turmella heidän kuolemattomia sielujaan?

Mahdollisesti, mutta se ei oikeastaan ole kvadraattisen yhtälön vika. Itse asiassa kvadraattisella yhtälöllä on ollut keskeinen rooli paitsi koko ihmiskunnan sivilisaatiossa sellaisena kuin me sen tunnemme, myös muiden avaruusolentojen sivilisaatioiden mahdollisessa havaitsemisessa ja jopa sellaisissa elintärkeissä nykyajan toiminnoissa kuin satelliittitelevision katselu. Millä muulla, paitsi jumalallisen ilmoituksen luonteella, voitaisiin katsoa olleen tällainen vaikutus elämään sellaisena kuin me sen tunnemme? Kvadraattiset yhtälöt voivat todellakin hyvin todellisessa mielessä pelastaa henkesi.

Babylonialaiset

Kaikki alkoi noin 3000 eKr. babylonialaisista. He olivat yksi maailman ensimmäisistä sivilisaatioista ja keksivät hienoja ideoita, kuten maanviljelyn, kastelun ja kirjoittamisen. He piirsivät auringon, kuun ja planeettojen radat ja kirjasivat ne ylös savitauluille (joita voit yhä nähdä British Museumissa). Babylonialaisille olemme velkaa nykyaikaiset kulma-ajatukset, mukaan lukien tapa, jolla ympyrä jaetaan 360 asteeseen (pienen laskuvirheen vuoksi, yksi per päivä). Olemme babylonialaisille velkaa myös (pelätyn) verottajan keksinnön, joka on vähemmän miellyttävä. Ja tämä oli yksi syy siihen, että babylonialaiset tarvitsivat kvadraattisten yhtälöiden ratkaisemista.

Asettakaamme, että olet babylonialainen maanviljelijä. Jossain maatilallasi on neliönmuotoinen pelto, jolla kasvatat jotain satoa. Minkä määrän satoasi voit kasvattaa pellolla? Jos kaksinkertaistat pellon kummankin sivun pituuden, huomaat, että voit kasvattaa neljä kertaa niin paljon satoa kuin ennen. Tämä johtuu siitä, että viljeltävän sadon määrä on verrannollinen pellon pinta-alaan, joka puolestaan on verrannollinen sivun pituuden neliöön. Matemaattisesti ilmaistuna, jos on pellon sivun pituus, 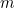on sadon määrä, jonka voit kasvattaa neliönmuotoisella pellolla, jonka sivupituus on 1, ja on sadon määrä, jonka voit kasvattaa, niin

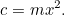Tämä on ensimmäinen kvadraattinen yhtälömme, alastomana ja auringonvalossa vilkkuen. Kvadraattiset yhtälöt ja pinta-alat liittyvät toisiinsa kuin sisarukset samaan perheeseen. Tällä hetkellä meidän ei kuitenkaan tarvitse ratkaista mitään – ennen kuin verottaja saapuu! Iloisesti hän sanoo maanviljelijälle: ”Haluan, että annat minullesatoa maksaaksesi tilasi verot.” Maanviljelijällä on nyt pulma: kuinka suuren pellon hän tarvitsee kasvattaakseen tuon määrän satoa? Me voimme vastata tähän kysymykseen helposti, itse asiassa

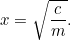Neliöjuurten löytäminen laskimen avulla on meille helppoa, mutta babylonialaisille se oli suurempi ongelma. Itse asiassa he kehittivät vastauksen peräkkäiseen approksimointiin perustuvan menetelmän, joka on identtinen algoritmin kanssa (nimeltään Newton-Raphson-menetelmä), jota nykyiset tietokoneet käyttävät paljon vaikeampien ongelmien kuin neliöyhtälöiden ratkaisemiseen.

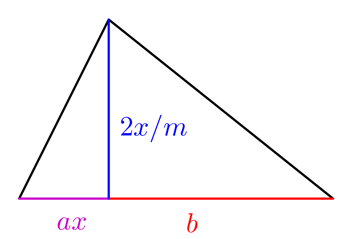
Nyt kaikki kentät eivät ole neliöitä. Oletetaan nyt, että maanviljelijällä on oudomman muotoinen pelto, jossa on kaksi kolmion muotoista osaa, kuten oikealla on esitetty.

Sopivilla :n ja :n arvoilla viljelijän tällä pellolla kasvattaman sadon määrä saadaan kaavalla

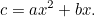Tämä näyttää paljon tutummalta kuin tuttu kvadraattinen yhtälö, ja jopa verottajan pahan silmän alla se on paljon vaikeampi ratkaista. Silti babylonialaiset keksivät taas vastauksen. Ensin jaetaan :lla, jolloin saadaan

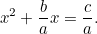Nyt täydennämme neliön käyttämällä hyväksi sitä tosiasiaa, että

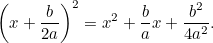Yhdistämällä tämä alkuperäiseen yhtälöön saadaan

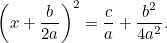Tämä on nyt yhtälö, jonka voimme ratkaista ottamalla neliöjuuret. Tuloksena on kuuluisa ”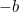-kaava”:

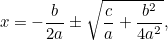, joka voidaan kirjoittaa uudelleen muodossa

(Kaavassa on yleensä ”-”.4ac”, koska kvadraattinen yhtälö kirjoitetaan tavallisemmin muodossa ””.)

Se, että neliöjuuren ottaminen voi antaa positiivisen tai negatiivisen vastauksen, johtaa siihen merkilliseen tulokseen, että kvadraattisella yhtälöllä on kaksi ratkaisua. Se siitä, että matemaattisilla arvoituksilla on vain yksi ratkaisu!

Nyt tähän loppuu usein kvadraattisten yhtälöiden opetus. Olemme saavuttaneet tuon kaikkien toimittajien rakastaman kohteen, kun he haastattelevat matemaatikkoja – kaavan. Voidaan keksiä loputtomasti kysymyksiä, joissa kaavaan laitetaan arvot ja , jolloin saadaan (kaksi) vastausta. Mutta tästä ei ole kyse matematiikassa lainkaan. Kaavan löytäminen on vain ensimmäinen askel pitkällä tiellä. Meidän on kysyttävä, mitä kaava tarkoittaa; mitä se kertoo meille maailmankaikkeudesta; onko kaavalla todella merkitystä? Katsotaanpa nyt, mihin tämä kaava meidät vie.

Yllätys kreikkalaisille, vähän matemaattista origamia ja suhteellisuudentajua

Siirrymme nyt 1000 vuotta eteenpäin antiikin kreikkalaisiin ja katsomme, mitä he tekivät neliöyhtälöistä. Kreikkalaiset olivat loistavia matemaatikkoja ja löysivät suuren osan matematiikasta, jota käytämme vielä nykyäänkin. Yksi yhtälöistä, joiden ratkaisemisesta he olivat kiinnostuneita, oli (yksinkertainen) kvadraattinen yhtälö

He tiesivät, että tällä yhtälöllä oli ratkaisu. Itse asiassa se on sellaisen suorakulmaisen kolmion hypotenuusan pituus, jonka sivut olivat pituudeltaan yksi.

Pythagoraan lauseesta seuraa, että jos suorakulmainen-kulmikkaalla kolmiolla on lyhyemmät sivut ja ja hypotenuusa , niin

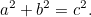Laitetaan 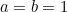ja , niin 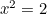. Siis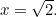

Mikä on siis tässä tapauksessa? Tai esittääksemme kreikkalaisten esittämän kysymyksen, millainen luku se on? Syy siihen, että tällä oli merkitystä, johtui kreikkalaisten suhteellisuudentajusta. He uskoivat, että kaikki luvut olivat suhteessa toisiinsa. Tarkalleen ottaen tämä tarkoitti, että kaikki luvut olivat murtolukuja muodossa 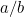, jossa ja ovat kokonaislukuja. Luvut kuten 1/2, 3/4 ja 355/113 ovat kaikki esimerkkejä murtoluvuista. Oli luonnollista olettaa, että myös oli murtoluku. Suuri yllätys oli, että se ei ole. Itse asiassa

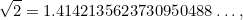, jossa pisteet tarkoittavat, että :n desimaalinen laajennus jatkuu äärettömään ilman havaittavaa mallia. (Tapaamme tämän tilanteen uudelleen myöhemmin, kun opimme kaaoksesta.)

oli ensimmäinen irrationaaliluku (eli luku, joka ei ole murtoluku eli rationaaliluku), joka tunnustettiin sellaiseksi. Muita esimerkkejä ovat 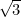,,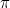 ja itse asiassa ”useimmat” luvut. Kesti 1800-luvulle asti, ennen kuin meillä oli hyvä tapa ajatella näitä lukuja. Keksintö, jonka mukaan ei ollut rationaaliluku, aiheutti sekä suurta innostusta (sen seurauksena uhrattiin 100 härkää) että suuren järkytyksen, ja löytäjän oli tehtävä itsemurha. (Olkoon tämä kauhea varoitus matemaattisesti innokkaille!) Tässä vaiheessa kreikkalaiset luopuivat algebrasta ja siirtyivät geometriaan.

Kaukana siitä, että se olisi tuntematon luku, tapaamme säännöllisesti: aina kun käytämme A4-paperia. Euroopassa paperin koko mitataan A-kokoina, joista A0 on suurin, ja sen pinta-ala on 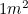. A-kokojen välillä on erityinen suhde. Jos nyt teemme vähän origamia, otamme A1-paperiarkin ja taittelemme sen kahtia (sen pisintä sivua pitkin), saamme A2-paperin. Taittamalla se uudelleen kahtia saadaan A3, sitten taas A4 jne. Paperi on kuitenkin suunniteltu niin, että jokaisen A-koon mittasuhteet ovat samat – eli jokaisella paperinpalalla on sama muoto.

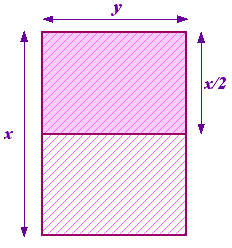
Voimme esittää kysymyksen, mikä tämä mittasuhde on. Aloitetaan paperinpalasta, jonka sivut ovat x ja y ja jonka pisin sivu on x. Nyt jaetaan tämä kahtia, jolloin saadaan toinen paperinpala, jonka sivut ovat y ja x/2, ja nyt y on pisin sivu. Tämä on esitetty kuvassa oikealla.

Ensimmäisen paperinpalan mittasuhteet ovat 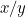ja toisen paperinpalan mittasuhteet ovat 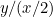tai 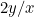. Haluamme näiden kahden mittasuhteen olevan yhtä suuret. Tämä tarkoittaa, että

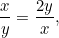tai

Taas yksi kvadraattinen yhtälö! Onneksi se on sellainen, jonka olemme jo tavanneet. Ratkaisemalla sen havaitsemme, että

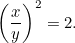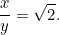Tämä tulos on helppo tarkistaa. Ota vain A4- (tai A3- tai A5-) paperiarkki ja mittaa sivut. Voimme myös laskea kunkin arkin koon. A0-paperin pinta-ala 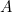saadaan kaavalla

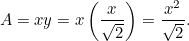Mutta tiedämme, että 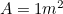joten meillä on toinen kvadraattinen yhtälö A0:n pisimmälle sivulle , jonka antaa

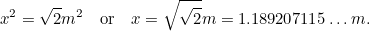Tämä tarkoittaa, että A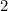:n pisin sivu 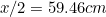(miksi?) ja A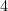:n 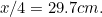. Tarkista nämä omilta paperiarkiltasi.

Yhdysvalloissa käytetyllä paperilla, jota kutsutaan foolscapiksi, on erilainen suhde. Nähdäksemme miksi, palaamme kreikkalaisiin ja toiseen kvadraattiseen yhtälöön. Aiheutettuaan niin paljon murhetta kvadraattinen yhtälö lunastaa paikkansa täydellisten mittasuhteiden etsinnässä: etsintä, joka jatkuu vielä nykyäänkin elokuvakalusteiden suunnittelussa, ja se on nähtävissä monissa luonnon osa-alueissa.

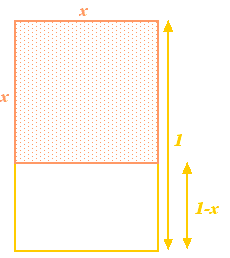
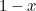Aloitetaan suorakulmiosta ja poistetaan siitä neliö, jonka sivun pituus on sama kuin suorakulmion lyhimmän sivun pituus. Jos suorakulmion pisimmän sivun pituus on 1 ja lyhimmän sivun pituus , neliön sivujen pituus on . Poistamalla se suorakulmiosta saadaan pienempi suorakulmio, jonka pisin sivu on ja pienin sivu . Niin pitkälle, niin abstraktia. Kreikkalaiset kuitenkin uskoivat, että esteettisimmät mittasuhteet omaava suorakulmio (niin sanottu kultainen suorakulmio) oli se, jonka edellä konstruoidulla suurella ja pienellä suorakulmiolla oli samat mittasuhteet. Jotta tämä olisi mahdollista, meidän on oltava

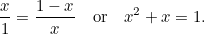Tämä on jälleen yksi kvadraattinen yhtälö: hyvin tärkeä yhtälö, joka tulee vastaan kaikenlaisissa sovelluksissa. Sen (positiivinen) ratkaisu on

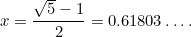Luku on nimeltään kultainen leikkaus ja sitä merkitään usein kreikkalaisella kirjaimella .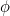

Kultainen suorakulmio näkyy ikkunoiden muodossa erityisesti georgialaisissa taloissa. Viime aikoina kultainen leikkaus löytyy myös valokuvien ja elokuvakuvien ”täydellisenä muotona”. Nelikulmioyhtälö 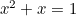esiintyy myös jänispopulaatioita koskevissa tutkimuksissa sekä kuvioissa, joihin auringonkukkien siemenet ja kasvien varsien lehdet asettuvat. Nämä kaikki liittyvät kultaiseen leikkaukseen Fibonacci-sarjan kautta, joka saadaan kaavalla

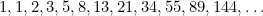Auringonkukan siemenet, järjestetty käyttäen Fibonaccin lukuja

Parthenon, joka ilmentää kultaista leikkausta

Tässä järjestyksessä jokainen termi on kahden edellisen termin summa. Fibonacci löysi sen 1400-luvulla yrittäessään ennustaa kanien tulevaa populaatiota. Jos otat kunkin termin suhteen sitä seuraavaan, saat lukujonon

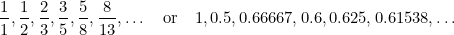ja nämä luvut lähestyvät yhä enemmän ja enemmän (arvasitkin) kultaista leikkausta .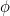

Etsimällä edellä olevan neliöyhtälön molemmat juuret voimme itse asiassa löytää kaavan Fibonaccin sarjan n:nnelle termille. Jos on 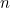:nnen tällaisen luvun kanss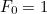a ja 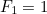, niin saadaan kaavalla

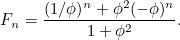Konics yhdistää kvadraattiset yhtälöt tähtiin

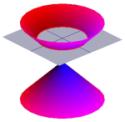
Myös kreikkalaiset olivat hyvin kiinnostuneita kartioiden muodosta. Vasemmalla olevassa kuvassa on tyypillinen kartio.

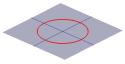
Kartiosta puolet voidaan visualisoida taskulampusta tulevan valon leviämisenä. Jos nyt valotat taskulampulla tasaista pintaa, kuten seinää, näet erilaisia muotoja, kun liikutat taskulamppua ympäriinsä. Näitä muotoja kutsutaan kartioleikkauksiksi, ja ne ovat käyriä, jotka saadaan, jos kartiota leikataan eri kulmista. Kreikkalaiset tutkivat juuri näitä käyriä ja havaitsivat, että kartioleikkauksia on periaatteessa neljää eri tyyppiä. Jos kartion läpi otetaan vaakasuora leikkaus, saadaan ympyrä. Jos leikkaus tehdään pienessä kulmassa vaakatasoon nähden, saadaan ellipsi. Jos otetaan pystysuora poikkileikkaus, saadaan hyperbeli, ja jos otetaan poikkileikkaus kartion yhden sivun suuntaisesti, saadaan paraabeli. Nämä käyrät on esitetty alla.

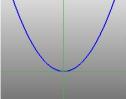
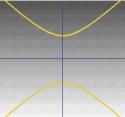
Ristikkäis…kartion poikkileikkaus voi olla ympyrä …	… ellipsi …	… paraabeli …	…. tai hyperbola.

Koniset leikkaukset tulevat kertomukseemme, koska kutakin niistä kuvaa neliöllinen yhtälö. Erityisesti, jos 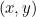edustaa kunkin käyrän pistettä, niin kvadraattinen yhtälö yhdistää ja 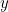. Meillä on:

Ympyrä: ;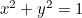

Ellipsi: ;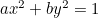

Hyperbel: ;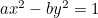

Parabeli: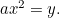

Näitä käyriä tunnettiin ja tutkittiin jo kreikkalaisista lähtien, mutta ympyrää lukuun ottamatta niillä ei näyttänyt olevan mitään käytännön sovelluksia. Kuten näemme seuraavassa Plussan numerossa, kvadraattisten yhtälöiden ja kartioiden välinen yhteys yhdistettynä mahtavaan onnekkaaseen sattumaan johti kuitenkin ymmärrykseen maailmankaikkeuden toiminnasta, ja 1500-luvulla koitti aika, jolloin kartiot muuttivat maailmaa.

Tekijöistä

Chris Budd on Bathin yliopiston matemaattisten tieteiden laitoksen soveltavan matematiikan professori ja Lontoon Royal Institutionin matematiikan professori.

Chris Sangwin työskentelee Birminghamin yliopiston matematiikan ja tilastotieteen laitoksella. Hän on tutkijana matematiikan, tilastotieteen ja operaatiotutkimuksen oppimisen ja opetuksen tukiverkoston keskuksessa.

He ovat hiljattain kirjoittaneet suositun matematiikkakirjan Mathematics Galore!, jonka on julkaissut Oxford University Press.

Tämän artikkelin innoittajaksi on osittain otettu Britannian parlamentin alahuoneessa käyty merkittävä keskustelu kvadraattisista yhtälöistä. Pöytäkirja tästä keskustelusta löytyy Hansard, United Kingdom House of Commons, 26 June 2003, Columns 1259-1269, 2003, joka on saatavilla verkossa House of Commons Hansard Debate -sivustolla.