Neljäsluokkalainen Alice kysyy: ”Kuinka monta lävistäjää on kymmenkulmassa?”
Hyvä kysymys, Alice. Mutta sen sijaan, että antaisin sinulle vastauksen tuohon kysymykseen, näytän sinulle, miten voit selvittää sen itse. Enkä vain sitä, vaan näytän, miten voit selvittää vastauksen mille tahansa monikulmiolle, vaikka siinä olisi 20, 50 tai 2000 sivua!
Valmiina? Aloitetaan yksinkertaisella esimerkillä. Otetaan monikulmio, jolla on 8 sivua (jota kutsutaan kahdeksankulmioiksi), näin:
Nyt, koska tällä monikulmiolla on kahdeksan sivua, sillä on myös kahdeksan kärkeä. Tuntuu hieman ylivoimaiselta yrittää selvittää kaikki lävistäjät, joten keskitytään vain yhteen kärkeen. Kuinka monta lävistäjää voit piirtää kahdeksankulmioon, jotka kaikki alkavat yhdestä kärjestä?
Vastaus tähän kysymykseen on viisi. Katso alla olevaa kaaviota:

Tässä kaaviossa olen valinnut diagonaalin vasemmalle heti ylimmän kärkipisteen alapuolelle, ja olen piirtänyt diagonaalit jokaiseen kärkipisteeseen, johon voin piirtää diagonaalin. Mihin diagonaaleihin en voi piirtää diagonaaleja? No, en voi piirtää diagonaalia kärkipisteestä takaisin itseensä, enkä voi piirtää diagonaaleja kahteen kärkipisteen vieressä olevaan kärkeen (koska ne eivät olisi diagonaaleja, vaan sivuja!).
On siis kolme kärkeä, joihin en voi piirtää diagonaaleja kyseisestä kärkipisteestä. Kahdeksan kärkeä yhteensä, miinus ne kolme, joihin en voi piirtää, jää viisi. Tämä on tärkeää muistaa: vähennä 3 kärkipisteiden lukumäärästä, niin saat niiden diagonaalien lukumäärän, joita voit piirtää mistä tahansa kärkipisteestä.
Mutta se on vain yksi kärkipiste! Voisithan piirtää diagonaaleja mistä tahansa kärjestä? Totta kai! Ja kahdeksankulmioissamme on kahdeksan kärkeä, joten otamme diagonaalien lukumäärän jokaista kärkeä kohti ja kerromme sen kärkien lukumäärällä: 5 x 8 = 40.
Saatat ajatella, että se on vastauksemme, mutta se ei ole. Miksei? Koska olemme laskeneet jokaisen lävistäjän kahdesti! Jokaisella diagonaalilla on kaksi kärkeä, joten olemme laskeneet sen toisesta päästä, ja olemme laskeneet sen myös toisesta päästä. Saadaksemme todellisen lävistäjien lukumäärän meidän on jaettava vastauksemme kahdella. 40 / 2 = 20. Kahdeksankulmion lävistäjiä on kaksikymmentä.
Kokeillaan tätä päättelyä monikulmiolla, jolla on 2000 sivua. Nyt en aio piirtää teille 2000-kulmion kulmaa, vaan meidän on selvitettävä päättely ilman kuvaa.
- Valitaan yksi kärki. Kuinka monta lävistäjää voit piirtää tuosta kärjestä? Vastaus: 2000 – 3 = 1997.
- Miten monta kärkeä yhteensä? Vastaus: 2000
- Miten monta lävistäjää lasketaan kaikista kärkipisteistä? Vastaus: Kertokaa, kuinka monta vertikaalia on laskettu ja kuinka monta on laskettu: 1997 x 2000 = 3,994,000
- Oops! Olemme laskeneet jokaisen diagonaalin kahdesti! Miten pääsemme eroon kaksoiskappaleista? Vastaus:
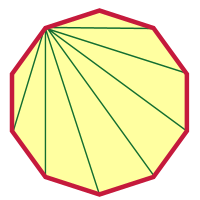
Kun on tehty jotain niinkin hullua kuin 2000-gon, kymmenkulmion ei pitäisi tuntua niin vaikealta, eikö? Minä panen sinut alkuun, ja sinä voit lopettaa sen tästä. Valitsin kärkipisteen ja piirsin siitä diagonaalit.
Kuinka monta niitä on? Pystyitkö päättelemään montako niitä on katsomatta kuvaa?
Pystytkö päättelemään sen tästä? Toivottavasti onnistuu! Onnea matkaan, Alice.
Sivumennen sanoen, on olemassa kaava, jota voit käyttää; se näyttää tältä: D = n(n – 3)/2. Mutta rehellisesti sanottuna en odota oppilaideni painavan sitä ulkoa. Odotan heidän muistavan, miten me päättelemme sen tässä. Jos ymmärrät logiikan, se on jopa parempi kuin kaava!