Fysiikka

Energian säilymislaki

Energia, kuten olemme huomanneet, säilyy, mikä tekee siitä yhden tärkeimmistä fysikaalisista suureista luonnossa. Energian säilymislaki voidaan esittää seuraavasti:

Kokonaisenergia on vakio missä tahansa prosessissa. Se voi muuttua muodoltaan tai siirtyä järjestelmästä toiseen, mutta kokonaismäärä pysyy samana.

Olemme tutustuneet joihinkin energian muotoihin ja joihinkin tapoihin, joilla sitä voidaan siirtää järjestelmästä toiseen. Tämä tutkimus johti kahden tärkeimmän energiamuodon määrittelyyn – mekaanisen energian (KE + PE) ja ei-konservatiivisten voimien tekemän työn kautta siirtyvän energian (Wnc). Energialla on kuitenkin monia muitakin muotoja, jotka ilmenevät monin eri tavoin, ja meidän on pystyttävä käsittelemään kaikki nämä ennen kuin voimme kirjoittaa yhtälön edellä esitetylle energian säilymistä koskevalle yleiselle lausumalle.

Muut energiamuodot kuin mekaaninen energia

Tässä vaiheessa käsittelemme kaikkia muita energiamuotoja niputtamalla ne yhteen ryhmään, jota kutsutaan muuksi energiaksi (OE). Tällöin voimme esittää energian säilymisen yhtälön muodossa seuraavasti: KEi + PEi +Wnc +OEi = KEf + PEf + OEf.

Kaikki energian ja työn muodot voidaan sisällyttää tähän hyvin yleiseen energian säilymistä koskevaan lausumaan. Kineettinen energia on KE, konservatiivisen voiman tekemää työtä edustaa PE, ei-konservatiivisten voimien tekemää työtä Wnc, ja kaikki muut energiat sisältyvät OE:hen. Tämä yhtälö pätee kaikkiin aiempiin esimerkkeihin; niissä tilanteissa OE oli vakio, joten se vähennettiin pois eikä sitä otettu suoraan huomioon.

Milloin OE:llä on merkitystä? Yksi esimerkki tapahtuu, kun ihminen syö. Ruoka hapettuu, jolloin vapautuu hiilidioksidia, vettä ja energiaa. Osa tästä kemiallisesta energiasta muuttuu liike-energiaksi, kun ihminen liikkuu, potentiaalienergiaksi, kun ihminen muuttaa korkeutta, ja lämpöenergiaksi (toinen OE:n muoto).

Joitakin energian monista muodoista

Mitä muita energian muotoja on? Voit luultavasti nimetä useita energiamuotoja, joita ei ole vielä käsitelty. Monia niistä käsitellään myöhemmissä luvuissa, mutta esitellään tässä muutamia yksityiskohtaisesti. Sähköenergia on yleinen energiamuoto, jota muunnetaan moniksi muiksi energiamuodoiksi ja joka toimii monenlaisissa käytännön tilanteissa. Polttoaineet, kuten bensiini ja ruoka, sisältävät kemiallista energiaa, joka voidaan siirtää järjestelmään hapettamalla. Kemiallinen polttoaine voi tuottaa myös sähköenergiaa, kuten paristoissa. Akut voivat puolestaan tuottaa valoa, joka on hyvin puhdas energiamuoto. Suurin osa maapallon energialähteistä on itse asiassa varastoitua energiaa, joka on peräisin auringosta saamastamme energiasta. Tätä kutsutaan joskus säteilyenergiaksi tai sähkömagneettiseksi säteilyksi, johon kuuluvat näkyvä valo, infrapuna ja ultraviolettisäteily. Ydinenergia on peräisin prosesseista, joissa mitattavat massamäärät muutetaan energiaksi. Ydinenergiaa muunnetaan auringonvalon energiaksi, sähköenergiaksi voimalaitoksissa sekä lämmönsiirron ja räjähdyksen energiaksi aseissa. Kaikkien esineiden sisällä olevat atomit ja molekyylit ovat satunnaisessa liikkeessä. Tätä satunnaisliikkeistä syntyvää sisäistä mekaanista energiaa kutsutaan lämpöenergiaksi, koska se liittyy kappaleen lämpötilaan. Nämä ja kaikki muut energiamuodot voidaan muuntaa toisiinsa ja niillä voidaan tehdä työtä.

Taulukossa 1 on esitetty eri kohteisiin ja eri ilmiöihin varastoituneen, käytetyn tai vapautuneen energian määrä. Energioiden kirjo sekä energiamuotojen ja -tilanteiden moninaisuus on vaikuttava.

Energian muuntuminen

Energian muuntaminen yhdestä muodosta toiseen tapahtuu koko ajan. Ruoan kemiallinen energia muuttuu lämpöenergiaksi aineenvaihdunnan kautta; valoenergia muuttuu kemialliseksi energiaksi fotosynteesin kautta. Laajemmassa esimerkissä hiilen sisältämä kemiallinen energia muuttuu lämpöenergiaksi, kun se palamalla muuttaa veden höyryksi kattilassa. Höyryn lämpöenergia puolestaan muunnetaan mekaaniseksi energiaksi, kun se pyörittää turbiinia, joka on kytketty generaattoriin sähköenergian tuottamiseksi. (Kaikissa näissä esimerkeissä kaikki alkuperäinen energia ei muutu mainituiksi energiamuodoiksi. Tätä tärkeää seikkaa käsitellään myöhemmin tässä jaksossa.)

Toinen esimerkki energian muuntamisesta tapahtuu aurinkokennossa. Aurinkokennoon (ks. kuva 1) osuva auringonvalo tuottaa sähköä, jota puolestaan voidaan käyttää sähkömoottorin käyttämiseen. Energia muunnetaan ensisijaisesta aurinkoenergialähteestä sähköenergiaksi ja sitten mekaaniseksi energiaksi.

.

Taulukko 1. Erilaisten kohteiden ja ilmiöiden energia
Kohde/ilmiö	Energia jouleina
Big Bang	1068
Supernovassa vapautuva energia	1044
Maailman valtamerten kaiken vedyn fuusio	1034
Maailman vuotuinen energiankulutus	4 × 1020
Suuri fuusiopommi (9 megatonnia)	3.8 × 1016
1 kg vetyä (fuusio heliumiksi)	6.4 × 1014
1 kg uraania (ydinfissio)	8.0 × 1013
Hiroshiman kokoinen fissiopommi (10 kilotonnia)	4.2 × 1013
90 000 tonnin lentotukialus 30 solmun nopeudella	1,1 × 1010
1 tynnyri raakaöljyä	5.9 × 109
1 tonni TNT	4.2 × 109
1 gallona bensiiniä	1.2 × 108
Kodin päivittäinen sähkönkulutus (kehittyneet maat)	7 × 107
Aikuisen päivittäinen ruoan saanti (suositus)	1,2 × 107
1000 kg:n painoinen auto 90 km/h:n nopeudella	3.1 × 105
1 g rasvaa (9,3 kcal)	3,9 × 104
ATP-hydrolyysireaktio	3.2 × 104
1 g hiilihydraattia (4,1 kcal)	1,7 × 104
1 g proteiinia (4.1 kcal)	1.7 × 104
Tennispallo nopeudella 100 km/h	22
Mosquito (10-2 g nopeudella 0.5 m/s)	1.3 × 10-6
Yksittäinen elektroni televisioputken sädehidastuksessa	4. Energian muuntoprosessin hyötysuhde Eff määritellään seuraavasti \displaystyle\text{Hyötysuhde}(Eff)=\frac{\text{hyödyllisen energian tai työn tuotos}{\text{kokonaisenergian panos}}=\frac{W_{\text{out}}}{E_{\text{in}}}\\\\\ Taulukossa 2 on lueteltu joitain mekaanisten laitteiden ja inhimillisten aktiviteettien hyötysuhteita. Esimerkiksi hiilivoimalassa noin 40 % hiilen kemiallisesta energiasta muuttuu käyttökelpoiseksi sähköenergiaksi. Loput 60 % muuttuu muiksi (ehkä vähemmän hyödyllisiksi) energiamuodoiksi, kuten lämpöenergiaksi, joka sitten vapautuu ympäristöön palamiskaasujen ja jäähdytystornien kautta. Taulukko 2. Ihmiskehon ja mekaanisten laitteiden hyötysuhde Toiminta/laite Hyötysuhde (%) Pyöräily ja kiipeily 20 Uinti, pinta 2 Uinti, vedenalainen 4 Lapiointi 3 Painonnosto 9 Höyrykone 17 Bensamoottori 30 Dieselmoottori 35 Ydinvoimalat 35 Hiilivoimalaitos 42 Sähkömoottori 98 Kompakti loisteputkivalo 20 Gasulämmitin (kotitalous) 90 Aurinkokenno 10 PhET Explorations: Massat ja jouset Realistinen massa- ja jousilaboratorio. Ripustetaan massoja jousiin ja säädetään jousen jäykkyyttä ja vaimennusta. Voit jopa hidastaa aikaa. Kuljeta laboratorio eri planeetoille. Kaavio näyttää kunkin jousen liike-, potentiaali- ja lämpöenergiat. 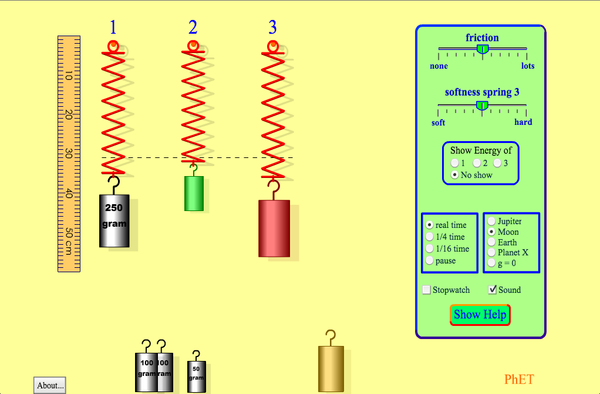Klikkaa ja suorita simulaatio. Yhteenveto Energian säilymislaki sanoo, että kokonaisenergia on vakio missä tahansa prosessissa. Energia voi muuttua muodoltaan tai siirtyä systeemistä toiseen, mutta kokonaismäärä pysyy samana. Kun otetaan huomioon kaikki energiamuodot, energian säilymislaki kirjoitetaan yhtälön muotoon KEi + PEi + Wnc + OEi = KEf + PEf + OEf, jossa OE on kaikki muut energiamuodot mekaanisen energian lisäksi. Yleisesti esiintyviä energiamuotoja ovat sähköenergia, kemiallinen energia, säteilyenergia, ydinenergia ja lämpöenergia. Energiaa hyödynnetään usein työn tekemiseen, mutta systeemin kaikkea energiaa ei ole mahdollista muuttaa työksi. Koneen tai ihmisen hyötysuhde Eff määritellään seuraavasti: \text{Eff}=\frac{{W}_{\text{out}}}{{E}_{\text{in}}}\\\\, missä Wout on hyödyllinen tuotettu työ ja Ein on kulutettu energia. Konseptuaaliset kysymykset Harkitse seuraavaa skenaariota. Auto, jolle kitka ei ole häviävän pieni, kiihtyy levosta alas mäkeä ja bensiini loppuu lyhyen matkan jälkeen. Kuljettaja antaa auton rullata edelleen mäkeä alaspäin, sitten ylös ja pienen harjanteen yli. Sitten hän ajaa mäkeä alas huoltoasemalle, jossa hän jarruttaa pysähtymiseen ja täyttää tankin bensiinillä. Tunnista, mitä energiamuotoja autossa on ja miten ne muuttuvat ja siirtyvät tässä tapahtumasarjassa. (Katso kuva 2.) Kuva 2. Auto, jossa kitka ei ole mitätön, kulkee mäkeä alaspäin, pienen harjanteen yli, sitten taas alamäkeen ja pysähtyy huoltoasemalle. Auto, jossa kitka ei ole mitätön, kulkee mäkeä alaspäin, pienen harjanteen yli, sitten taas alamäkeen ja pysähtyy huoltoasemalle. Auto kulkee mäkeä alaspäin, kulkee harjanteen yli, sitten taas alamäkeen ja pysähtyy lopulta huoltoasemalle. Kukin näistä paikoista on merkitty alaspäin osoittavalla nuolella. Kuvaa keihään energiansiirrot ja -muodonmuutokset alkaen siitä, kun urheilija nostaa keihään, ja päättyen siihen, kun keihäs juuttuu maahan heiton jälkeen. Rikkovatko laitteet, joiden hyötysuhde on alle yksi, energian säilymislakia? Selitä. Luettele neljä eri energiamuotoa tai -tyyppiä. Anna yksi esimerkki muuntumisesta kustakin näistä muodoista toiseen muotoon. Luettele energiamuunnokset, jotka tapahtuvat polkupyörällä ajettaessa. Ongelmat &Harjoitukset Taulukon 1 arvoja käyttäen, kuinka monta DNA-molekyyliä voitaisiin rikkoa vanhanmallisen televisiolähetysputken sädettä säteen kuljettamalla energialla? (Nämä elektronit eivät sinänsä olleet vaarallisia, mutta ne synnyttivät vaarallisia röntgensäteitä.) Myöhemmissä putkitelevisiomalleissa oli suojaus, joka imi röntgensäteet ennen kuin ne pääsivät pakenemaan ja altistivat katsojia.) Osoita, että 20,0 m:n korkeudella vedenpinnan yläpuolella olevalta sillalta 15 m:n alkunopeudella heitetty kivi, jonka nopeus on 15,0 m:n korkeudella vedenpinnan yläpuolella.0 m/s iskeytyy veteen nopeudella 24,8 m/s riippumatta heittosuunnasta. Jos fuusiopommien energiaa käytettäisiin maailman energiantarpeen tyydyttämiseen, kuinka monta 9 megatonnin pommia tarvittaisiin vuoden energiantarpeen tyydyttämiseen (käyttäen taulukon 1 tietoja)? Tämä ei ole niin kaukaa haettua kuin miltä se saattaa kuulostaa – ydinpommeja on tuhansia, ja niiden energia voidaan vangita maanalaisiin räjähdyksiin ja muuntaa sähköksi, kuten luonnollinen geoterminen energia. (a) Vetyfuusion käyttäminen energiantoimituksiin on unelma, joka saattaa toteutua ensi vuosisadalla. Fuusio olisi suhteellisen puhdas ja lähes rajaton energianlähde, kuten taulukosta 1 käy ilmi. Tämän havainnollistamiseksi laskekaa, kuinka monta vuotta maailman nykyistä energiantarvetta voitaisiin tyydyttää yhdellä miljoonasosalla valtamerten vetyfuusioenergiasta. (b) Miten tämä aika vertautuu historiallisesti merkittäviin tapahtumiin, kuten vakaiden talousjärjestelmien kestoon? Sanasto Energian säilymislaki: Yleinen laki, jonka mukaan kokonaisenergia on vakio missä tahansa prosessissa; energia voi muuttua muodoltaan tai siirtyä systeemistä toiseen, mutta kokonaisuus pysyy samana Sähköenergia: varausvirran kuljettama energia kemiallinen energia: atomien ja molekyylien välisiin sidoksiin varastoitunut aineen energia, joka voidaan vapauttaa kemiallisessa reaktiossa säteilyenergia: sähkömagneettisten aaltojen kuljettama energia ydinenergia: Energia, joka vapautuu atomiytimissä tapahtuvista muutoksista, kuten kahden kevyen ytimen fuusiosta tai raskaan ytimen fissiosta lämpöenergia: Kappaleen sisällä oleva, sen atomien ja molekyylien satunnaisesta liikkeestä johtuva energia, joka selittää kappaleen lämpötilan tehokkuus: mitta, jolla mitataan työn tekemiseen käytetyn energian tehokkuutta; hyötyenergia tai työ jaettuna energian kokonaispanoksella Valittuja ratkaisuja ongelmiin & Harjoituksia 1. 4 × 104 molekyyliä 2. Yhtälöitämällä ΔPEg ja ΔKE saadaan v=\sqrt{2gh+v_0^2}=\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(15.0\text{ m/s}\right)^2}=24.8\text{ m/s}\\\ 4. (a) 25 × 106 vuotta; (b) Tämä on paljon, paljon pidempi kuin ihmisen aikaskaala. Esittelyarvot ↵ .