YLEISKEMIAN TEEMAT
Energia: Peruskäsitteet
Energian muodot: Kineettinen ja potentiaalinen.Työ ja energia.Lämpö ja lämpötila.Sähköstaattinen potentiaalienergia.
Energia: kineettinen ja potentiaalinen
Energian käsite on fysikaalisten tieteiden peruskäsite. Tässä pyrimme esittämään joitakin energiaan liittyviä ensimmäisiä periaatteita ja esittelemään joitakin energian ilmenemismuotoja, jotka ovat erityisen tärkeitä kemian kannalta. Ensinnäkin on usein hyvin hyödyllistä määritellä systeemi siten, että sillä tarkoitetaan tiettyä osaa maailmankaikkeudesta, josta havaintojamme tehdään. Systeemi koostuu esineestä tai esinekokoelmasta, ja se eroaa muusta maailmankaikkeudesta – jota kutsumme ympäristöksi – todellisen tai kuvitteellisen rajan avulla.
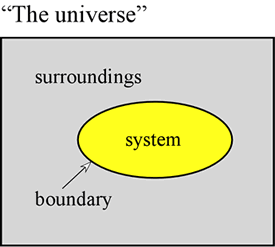
Kiinteässä tilavuudessa, kuten metallisylinterissä, pidetty kaasunäyte on esimerkki systeemistä – systeemistä, jolla on merkitystä meille, kun ryhdymme tutkimaan kaasujen yleisiä ominaisuuksia. Muita esimerkkejä ovat kaasunäyte ilmapallon sisällä tai polttoseos sylinterissä, jossa on mäntä. Molemmissa tapauksissa systeemiä ympäröi fysikaalinen, mutta liikkuva raja, joten systeemin tilavuus ei ole kiinteä. Toinen esimerkki, jota tarkastelemme usein, on liuennut aineseos, joka käy läpi kemiallista reaktiota koeputkessa tai dekantterilasissa. Tässä esitelty terminologia on erityisen tärkeää tutkittaessa sitä, miten energia ilmenee kemiallisissa systeemeissä, mikä kuuluu suurelta osin termodynamiikan alaan.
Yleisessä kemiassa tarkastelemamme systeemit ovat tyypillisesti levossa, ja painovoiman vaikutukset jätetään huomiotta. Usein olemme eniten kiinnostuneita systeemeistä, joissa tapahtuu kemiallisia reaktioita, jolloin systeemin kemiallinen koostumus muuttuu ajan myötä. Otetaan kuitenkin toistaiseksi laajempi näkökulma ja käytetään mekaanisia järjestelmiä, kuten heilurin heilahtelua tai biljardipallojen vierimistä ja törmäilyä, auttamaan meitä ymmärtämään energiaan liittyviä yleisiä periaatteita.
Systeemillä voidaan sanoa olevan energiaa kahdella eri tavalla, joita kutsumme kineettiseksi ja potentiaaliseksi energiaksi. Kineettinen energia on liikkeessä olevan aineen energiaa. Fysiikka tarjoaa tarkan matemaattisen määritelmän liike-energialle (KE), joka esitetään yhtälössä (alla vasemmalla).
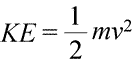
Tässä kappaleen liike-energia esitetään kappaleen massan (m) ja sen nopeuden neliön (v) tulona, joka kerrotaan myös vakiolla ½. Jos systeemi koostuu useammasta kuin yhdestä kappaleesta, kineettinen kokonaisenergia on ilmaistavissa yksittäisten kappaleiden kineettisten energioiden summana.
Voidaan johtaa energian yksiköt tämän määritelmän perusteella. Energian SI-yksikkö on joule (J), joka määritellään seuraavasti:
1 J = 1 kg-m-s-2
Potentiaalienergia on systeemin energiaa, joka voidaan tyypillisesti muuntaa liike-energiaksi jossakin muodossa ja joka kykenee tuottamaan jossakin määrin määrän, jota kutsutaan työksi (jota käsitellään jäljempänä). Selkeä esimerkki potentiaalienergiasta on rakennuksen vierustalla oleva tiili. Tiilellä on tietty määrä potentiaalienergiaa sen korkeuden vuoksi – sen sijainnin vuoksi suhteessa painovoimakenttään. Jos annamme tiilelle tönäisyn niin, että se putoaa reunalta, se liikkuu spontaanisti pienemmän potentiaalipotentiaalienergian suuntaan, ja näin tehdessään se saa liike-energiaa. Toinen esimerkki on pariston sähköinen potentiaalienergia (joka ilmaistaan jännitteenä). Kun johdolla ja hehkulampulla tehdään virtapiiri, joka yhdistää pariston kaksi napaa, niiden välinen sähköpotentiaaliero saa johdossa olevat elektronit liikkumaan (liike-energia), jolloin syntyy sekä lämpöä että valoa.
Tärkeä energiaan liittyvä yleinen periaate on, että sitä ei voi luoda eikä tuhota. Tämä tunnetaan energian säilymislakina. Määrällisesti tämä tarkoittaa, että systeemissä, kuten putoavassa tiilessä tai kellon heilurissa, kineettisen ja potentiaalisen energian summa on vakio. Tämä on jossain määrin abstraktio, sillä todellisessa heilurissa osa energiasta häviää jatkuvasti kitkan vuoksi, ja heiluriin on lisättävä pieni määrä energiaa, jotta se pysyy heilumassa (ja kello toimii). Mutta jos otamme huomioon tämän ”menetetyn” energian (joka itse asiassa näkyy ympäröivien ilmamolekyylien lämpöenergian lisääntymisenä) huolellisilla kokeellisilla mittauksilla, havaitaan, että energia todellakin säilyy aina. Toinen varoitus on tiivistetty Einsteinin kuuluisaan yhtälöön E = mc2, joka ilmaisee massan ja energian perustavanlaatuisen vastaavuuden. Energian säilymislain yleisempi muoto, jota voidaan kutsua massan ja energian säilymislaiksi, ottaa huomioon tämän vastaavuuden. Palatakseni takaisin yleiseen kemiaan, tällaiset aineen ja energian vuorovaikutukset eivät tyypillisesti kuulu sen toimialaan, kun taas ydinreaktioiden ja radioaktiivisuuden tutkiminen kuuluu ydinfysiikan piiriin.
Jos tarkastelemme kemiallista reaktiota, jossa kemiallisiin muutoksiin liittyy lämmöntuottoa, herää kysymys: Entä energian säilyminen tässä tapauksessa? Vastaus on, että on olemassa eräänlainen potentiaalienergia, jota voimme kutsua kemialliseksi potentiaalienergiaksi (tai yksinkertaisesti kemialliseksi potentiaaliksi), jonka voidaan ajatella sijaitsevan reagoivien aineiden molekyylien koostumuksessa. Tämä potentiaalienergia muuttuu sitten energiaksi lämmön muodossa, mutta käy ilmi, että läsnä olevan energian nettomäärä pysyy vakiona, kunhan pystymme määrittelemään ja mittaamaan lämmöntuotannon. Jokapäiväinen esimerkki siitä, mitä voimme nyt ymmärtää kemialliseksi potentiaalienergiaksi, on bensiinimoottori, jossa bensiinin ja hapen seoksessa on piilevä energiamuoto. Tämä bensiinin ja hapen seoksessa oleva latentti energia kuluu auton liike-energian tuottamiseen.
Työ ja energia
Työ on toinen käsite, jolle fysiikassa voidaan antaa tarkka määritelmä. Lisäksi mekaniikan lait voidaan yhdistää energiaan työ-energia- lauseen avulla. Jalkapallon potku tai mikä tahansa muu vastaava esimerkki havainnollistaa ajatusta siitä, että kappaleen liike-energiaa voidaan lisätä voiman avulla. Työ-energialauseke, joka on tämän ajatuksen yleistys, voidaan esittää karkeasti seuraavasti: Kappaleen energian muutos on yhtä suuri kuin siihen vaikuttavan voiman suuruus kerrottuna etäisyydellä, jonka kautta voima vaikuttaa.
Systeemissä työn seurauksena tapahtuva energiamuutos voi olla systeemin kannalta katsottuna positiivinen tai negatiivinen. Systeemi voi tehdä työtä, tai ympäristö voi tehdä systeemille työtä. Jos systeemi tekee työtä, se menettää energiaa ympäristöön. Jos systeemille tehdään työtä, systeemin energia lisääntyy. Esimerkiksi kun kipinä sytyttää palamisseoksen sylinterissä, jossa on liikkuva mäntä, aiheuttaa järjestelmän nopean laajenemisen ja laajeneminen on mekaanisesti kytketty ympäristössä olevan tangon liikkeeseen, sylinterin järjestelmä tekee työtä ympäristölle ja menettää näin energiaa. Tämä on tietenkin osa sitä, miten polttomoottori muuntaa kemiallisen potentiaalienergian liikkeessä olevan auton liike-energiaksi.
Yksi työn ja energian teoreeman implikaatio koskee yksiköitä, nimittäin sitä, että työtä voidaan mitata samoissa yksiköissä kuin energiaa. Koska Newtonin toinen laki on voima = massa × kiihtyvyys, newton (N), SI-yksikkö voimalle, saadaan muotoon M × L × T -2, ja siten 1 N = 1 kg m s-2. Voiman ja etäisyyden suhde on M × L2 × T -2, joten energian SI-yksikkö, joule (J), määritellään seuraavasti: 1 J = 1 kg m2 s-2. Tässä vaiheessa sinun pitäisi varmistaa itsellesi, että liike-energian yhtälössä on sama yhdistelmä perussuureita massa (M), pituus (tai etäisyys, L) ja aika (T).
Lämpö ja lämpötila
Käytämme sanoja lämpö ja lämpötila melko usein ja puhumme usein lämmöstä energiamuotona. Meillä kaikilla on intuitiivinen käsitys siitä, mitä nämä asiat ovat, mutta tässä haluamme ajatella niitä tieteellisemmin ja antaa niille muodollisemmat määritelmät, jos voimme. Tämä on välttämätön alkusoitto lämpöä vastaavan energian kvantifioinnille ja sitä kautta mittauksille, joilla voidaan todentaa energian säilymislaki. Huomaamme, että systeemin lämpöenergiaa voidaan verrata systeemin muodostavien atomien ja molekyylien (kuten edellä on määritelty) yhteenlaskettuun liike-energiaan. Kappaleen tai järjestelmän lämpötila on itse asiassa muodostavien atomien ja/tai molekyylien keskimääräisen liike-energian mitta. (Huom. Lämpötila ei ole täsmälleen yhtä suuri kuin molekyylien keskimääräinen liike-energia, mutta se on suoraan verrannollinen siihen. Katso lisätietoja kineettisen molekyyliteorian verkkosivulta).
Yksi tapa havainnollistaa, mitä tarkoitamme lämmöllä ja lämpötilalla ja niiden välisellä erolla, on tarkastella biljardipalloanalogiaa. Joissakin yksinkertaisissa yhteyksissä biljardipallojen käyttäytyminen on riittävä malli atomien tai molekyylien kokoelmalle, kuten kaasunäytteelle. Aivan kuten biljardipallot, joihin on juuri osunut nopeasti liikkuva lyöntipallo, kaasun molekyylit liikkuvat ympäriinsä ja kimpoilevat toisistaan ja niitä sisältävän säiliön seinämistä. Biljardipallojen kineettinen kokonaisenergia, joka on vain kunkin pallon yksittäisten kineettisten energioiden summa, on analoginen kaasumolekyylien lämpöenergiasisällön kanssa. Biljardipelin alussa tapahtuvassa ”tauossa” lyöntipallon alkuperäinen liike-energia jakautuu kaikkien pöydällä olevien pallojen kesken. Jotkut liikkuvat melko nopeasti ja toiset eivät niin nopeasti, mutta biljardipallojen järjestelmän ”lämpö” tai ”lämpöenergia” on vain näiden liike-energioiden summa. Toisaalta biljardipallosysteemin lämpötila olisi verrannollinen pallojen kokonaisuuden keskimääräiseen liike-energiaan.
Elektrostaattinen potentiaalienergia
Elektrostaattisen vetovoiman ja hylkimisen laki eli Coulombin laki kuvaa varattuun kappaleeseen toisen varatun kappaleen läsnäolosta aiheutuvaa voimaa. Voima on helpointa laskea, kun varauksia voidaan käsitellä hyvin pieninä pistevarauksina. Varatun kappaleen ”tunteman” voiman suuruus on verrannollinen varausten tuloon (sähkövarauksen SI-yksikkö on Coulomb, C) ja kääntäen verrannollinen varausten välisen etäisyyden neliöön (r kuvassa oikealla). Voima on vetovoima (kuten painovoima, ja se on merkitty kuvassa sisäänpäin osoittavilla nuolenkärjillä), jos varaukset ovat merkiltään vastakkaisia, ja vastenmielinen, jos varaukset ovat samanmerkkisiä.
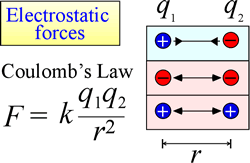
Kun voimat (kuten sähköstaattiset, magneettiset ja gravitaatiovoimat) voivat vaikuttaa etäisyydellä (avaruuden halki ilman mekaanista kosketusta), sanotaan tällaisten voimien alaisina olevien kohteiden olevan potentiaalisessa energiakentässä. Edellä puhuttiin gravitaatiopotentiaalienergiasta, ja vastaavasti sähköstaattisten voimien tapauksessa varautuneella esineellä on sähköstaattista potentiaalienergiaa sen vuoksi, että se sijaitsee sähkökentässä. Tällainen kenttä on olemassa minkä tahansa muun varauksen tai varausten läheisyydessä.
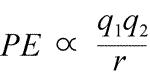
Elektrostaattisen potentiaalienergian yhtälö: PE on verrannollinen varauksiin q1 ja q2 ja kääntäen verrannollinen erotusetäisyyteen r. Potentiaalienergian funktion muoto seuraa matemaattisesti voiman lausekkeesta, Coulombin laista.
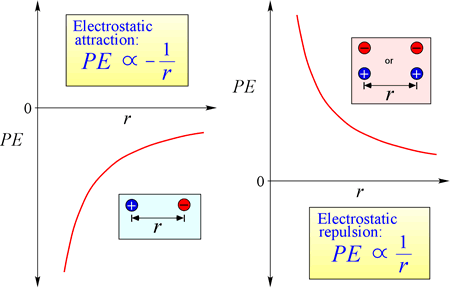
Vetovoimassa olevien varausten vastakkaisten etumerkkien vuoksi potentiaalienergia on aina negatiivinen, ja mitä lähemmäs varaukset lähestyvät toisiaan, sitä negatiivisemmaksi eli pienemmäksi potentiaalienergia tulee. Kun erotusetäisyys r lähestyy nollaa, potentiaalienergiasta tulee äärettömän negatiivista. Samanmerkkisillä varauksilla repulsioenergia on aina positiivinen, ja se muuttuu äärettömän positiiviseksi, kun erotusetäisyys, r lähestyy nollaa.
Elektrostaattinen potentiaalienergia on tärkeä näkökohta kemiassa. Ymmärrys atomin luonteesta, kemiallisesta sitoutumisesta ja molekyylien välisistä voimista ovat kaikki ehdottoman riippuvaisia siitä, että otetaan huomioon systeemin energiaan vaikuttavien varaus-varaus-vuorovaikutusten vaikutus.
Tärkeitä yksiköitä
Energia (SI-yksikkö) 1 joule = 1 J = 1 kg-m-s-2
Alkuperäisvaraus, e = 1,60218 × 10-19 C (coulombi, C)
Faradayn vakio: F = NAe = 9,64853 × 104 C-mol-1
Sähköpotentiaali: volttia, V 1 V = 1 J C-1