Olet epätoivoinen opiskelija, joka yrittää kirjoittaa viimeistä lukukausitehtävääsi ennen valmistumistasi. Haluat vain saada sen valmiiksi ja juhlia saavutustasi. Yhtäkkiä joku kävelee koppiin, jossa olet työskennellyt koko päivän. Tämä henkilö näyttää hyvin paljon sinulta, mutta sinulla ei ole aikaa miettiä, mistä on kyse, sillä hän ojentaa sinulle heti USB-aseman ja käskee sinun palauttaa asemalla olevan lukukausitehtävän. ”Sitten voit mennä juhlimaan”, hän sanoo hymyillen poistuessaan nopeasti läheiseen portaikkoon. Nouset ylös ja lähdet hänen peräänsä, mutta hän näyttää kadonneen.
Palaat takaisin työpöytääsi, avaat tutkielman tiedoston, luet sen nopeasti läpi ja, puristaen eettisen dilemmasi, lähetät tutkielman. Muutamaa päivää myöhemmin saat arvosanan: A+. Lähdet etsimään salaperäistä muukalaista, joka antoi sinulle tämän hienon paperin, ja päädyt takaisin portaikkoon. Kävelet sisään ja mietit, minne muukalainen on voinut mennä. Hetken tai kahden jälkeen lähdet pois. Kun kävelet sen kopin ohi, jossa olit raatanut niin kauan, näet itsesi! Sitten sinulle valkenee. Sinun täytyy antaa itsellesi paperi. Onneksi olit laittanut USB-muistitikun taskuusi, ja koska olet poikkeuksellisen epäsiisti opiskelija, sinulla on yhä samat housut jalassa. Kävelet koppiin, ojennat itsellesi USB-aseman, annat itsellesi ohjeet ja pakenet välittömästi takaisin portaikkoon, joka kuljettaa sinut takaisin nykyhetkeen.
Miten voit antaa itsellesi paperin, jota kukaan ei kirjoittanut? Miten sinun luovuttamasi paperi voi saada sinut luovuttamaan paperin?
Mitä ovat kausaalisilmukat?
Kausaalisilmukka on tapahtumasarja e1, … , en. Jokainen silmukan tapahtuma on yksi syy seuraavalle tapahtumalle. Viimeinen tapahtuma en on yksi ensimmäisen tapahtuman e1 syistä. Jos kausaalisilmukalla ei ole ulkoisia (silmukan ulkopuolisia) syitä tai vaikutuksia, kausaalisilmukka on suljettu kausaalisilmukka, muuten se on avoin kausaalisilmukka. Ajattele suljettuja kausaalisilmukoita kausaalisesti eristettyinä. Ajattele avoimia kausaalisilmukoita kausaalisesti sulautuneina.
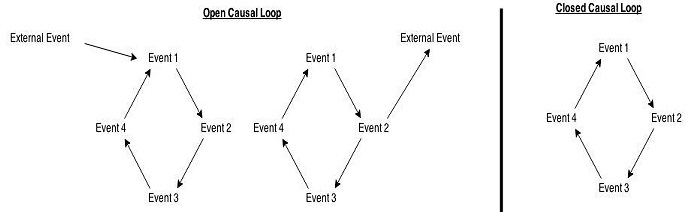
Kuva 1: Kahdenlaisia kausaalisilmukoita
Ovatko kausaalisilmukat mahdottomia?
Ajatus kausaalisilmukoista nähdään toisinaan sisältävän luontaisen paradoksin. Syyt tähän huoleen vaihtelevat.
Syy 1: Jokaiselle tapahtumalle on oltava aiheuttamaton ensimmäinen syy. Silmukat voivat syntyä ex nihilo (tyhjästä) näennäisesti ilman perimmäistä ensimmäistä syytä. Tämä huoli voidaan ratkaista vertaamalla kausaalisilmukoita tavallisempiin kausaaliketjuihin. Kausaaliketju on tapahtumien sarja, jossa jokainen tapahtuma aiheuttaa sarjan seuraavan tapahtuman (kausaalisilmukka on erityinen kausaaliketjun laji). Jotkin kausaaliketjut eivät ole silmukoita; ne koostuvat peräkkäisistä tapahtumista, joista kutakin seuraa ajallisesti seuraava tapahtuma ja jotka aiheuttavat sarjan seuraavan tapahtuman. Tässä määritelmässä ei ole mitään sellaista, joka edellyttäisi, että ketjulla olisi alku (tai loppu). Siksi tuntuu hieman oudolta vaatia, että kausaalisilmukan tapahtumat vaativat perimmäisen ensimmäisen syyn. Ainoa ero kausaaliketjujen ja kausaalisilmukoiden välillä on se, että seuratessaan kausaalisilmukkaa pitkin kausaatiota päädytään lopulta takaisin sinne, mistä lähdettiin liikkeelle.
Seuraavasti kausaalisilmukoilla on, ja näyttää jopa olevan pakko, olla ensimmäinen syy. Jokaisessa kausaalisilmukassa on ainakin yksi tapahtuma, joka tapahtuu aikaisemmin kuin kaikki muut. Tämä tapahtuma ei välttämättä aina osoittaudu joksikin perimmäiseksi ensimmäiseksi syyksi, joka selittää koko silmukan. Silti, koska alkutapahtuma tapahtuu ennen muita tapahtumia aikajanalla, se on ensimmäinen. Se on silmukan varhaisin tapahtuma.
Syy 2: Ympyräselityksen uhka. Tarkastellaan aiemmin kuin, suhdetta, joka usein liitetään tapahtumaan, joka aiheuttaa toisen tapahtuman. Perinteisesti tätä suhdetta pidetään transitiivisena; eli jos tapahtuma a on aikaisempi kuin tapahtuma b ja tapahtuma b on aikaisempi kuin tapahtuma c, niin silloin tapahtuma a on aikaisempi kuin tapahtuma c. Jos kuitenkin pidetään kausaalisuutta transitiivisena ja sovelletaan sitä kausaalisilmukan osalta, asiat hajoavat. Jos kausaatio on transitiivinen, jokainen tapahtuma kausaalisilmukassa on syy itselleen. Kolmen tapahtuman kausaalisilmukassa kausaatio toimii loistavasti sanottaessa, että tapahtuma a aiheuttaa b:n ja b aiheuttaa c:n ja c aiheuttaa a:n, mutta ellei kausaatio ole transitiivinen, nämä kolme tosiasiaa johtavat johtopäätökseen, että a aiheutti a:n. Se, että a aiheutti a:n, ei varmastikaan ole informatiivinen selitys a:lle. Onneksi vaikka kausaatio olisikin transitiivinen, meidän ei tarvitse olettaa, että vastaavien selittävien yhteyksien on säilyttävä. Ulrich Meyer (2012, 261) on sitä mieltä, että kaikkien paikallisten selitysten yhdistäminen johtaa heikompaan selitykseen.
Syy 3: Jokaiselle tapahtumaketjulle on oltava riittävä selitys sille, miksi ketjussa tapahtuu niin kuin tapahtuu. Jos jokaiselle tapahtumasekvenssille on oltava riittävä selitys, mahdollinen ongelma valottuu tarkastelemalla jinniä. Dzinni on esine, joka on osa silmukan tapahtumia ja joka näyttää syntyvän tyhjästä. Erinomainen esimerkki jinnistä on Swannin kaulakoru Timeriderista: The Adventure of Lyle Swann.
Tässä vuoden 1982 elokuvassa Swann lähetetään vahingossa ajassa taaksepäin ja hän tapaa Claire-nimisen naisen, joka lopulta viettelee hänet. Näyttävien tapahtumien jälkeen ihmiset, jotka vahingossa kuljettivat hänet ajassa taaksepäin, pelastavat Swannin. Juuri ennen hänen pelastumistaan Claire sieppaa kaulakorun, joka on periytynyt Swannille hänen iso-iso-isoäidiltään, joka varasti sen hänen iso-iso-isoisältään. Kaulakoru on jinni, koska Swann saa kaulakorun iso-iso-isoäidiltään, joka varasti häneltä saman kaulakorun vuosia aiemmin. Kuten arvata saattaa, Claire on Swannin iso-iso-isoäiti. Swann itse on hänen oma iso-iso-iso-isoisoisänsä.
Kaulakorun ja useimpien dzinnien aiheuttama ongelma on niiden olemassaolon lähde. Miten kaulakorun kaltainen fyysinen esine voi vain olla olemassa? Kuka on suunnitellut kaulakorun? Mikä selittää, miksi se on kaulakoru eikä vaikkapa rannekoru? Täytyy olla jokin selitys sille, miksi kaulakoru on sellainen kuin se on. Eikö?
Kaulakorun olemassaolon vaiheille on olemassa selityksiä. Kaulakorulla on syitä. Se, että Swann saa kaulakorun isoäidiltään, on syy siihen, että hän ottaa sen mukaansa ajassa taaksepäin. Kaulakorun siirtyminen ajassa taaksepäin on syy siihen, että Claire voi varastaa kaulakorun, ja niin edelleen. Lisäksi voidaan väittää, että maailmankaikkeudella ja luonnonlaeilla on oltava tietty rakenne, jotta kausaalisilmukoita voi olla olemassa. Näistä laeista löytyisi myös hyödyllisiä selityksiä.

Kuva 2: Timeriderin aikajana
Joitakin tosiasioita näyttää kuitenkin olevan pakko jättää selittämättä, sellaisia tosiasioita kuin se, että kaulakoru on kaulakoru eikä rannekoru. Lisäksi, miksi on olemassa kausaalisilmukka eikä mitään kausaalisilmukkaa? Osoittaako kyvyttömyytemme selittää näitä tosiasioita, että kausaalisilmukoissa on jotain epäjohdonmukaista? Ei; ongelma tässä päättelyssä on se, että samanlaisia ongelmia syntyy tavallisten esineiden kohdalla. Voit nähdä tuolin syyt, koska voit nähdä puusepän rakentavan tuolin puusta, mutta mikä teki puun? Vielä enemmän, mikä teki ne atomit, jotka muodostavat puun? Näitä kysymyksiä voi esittää jatkuvasti, mutta täysin riittävää ja täydellistä selitystä voi olla lähes mahdotonta saada aikaan normaalioloissa. On monia tosiasioita ja esineitä, joille emme ehkä koskaan löydä hyvää selitystä.
Vieksyäksemme tätä analyysia askeleen pidemmälle tarkastellaan kaulakorun taiteellisen muotoilun alkuperää. Kaulakoru vaikutti tavalliselta kaulakorulta, joka oli valmistettu tarkoituksella ja taidokkaasti. Tämä herättää kysymyksen siitä, mistä taiteellisuus oli peräisin. Kenen (tai minkä) taidoilla ja tiedoilla tämä kaulakoru luotiin? Storrs McCallin (2010) mukaan tähän ongelmaan ei ole ratkaisua. Ehkä joillekin tosiasioille ei yksinkertaisesti ole selitystä. Vaatimus siitä, että kaikelle on oltava selitys, ei ole perusteltu.
Tarvitseeko aikamatkailu kausaalisilmukoita?
Väite, jonka mukaan kaikkeen aikamatkailuun on sisällyttävä vähintään yksi kausaalisilmukka, on laajalti esitetty. Bradley Monton esittelee tätä kantaa vuonna 2009 aiheesta kirjoittamassaan esseessä käyttäen lainausta D.H. Mellorilta. Montonin mukaan Mellor argumentoi aikamatkailun mahdollisuutta vastaan ”’sulkemalla pois kausaalisilmukat… joita syklinen aika ja taaksepäin suuntautuva aikamatkailu tarvitsevat'” (Monton, 2009, 55; Mellor 1998, 131). Mellorin ja muiden mukaan, kun aikamatkustaja menee ajassa taaksepäin, hänen menneisyydessä tekemillään teoilla on aina vaikutuksia, jotka vaikuttavat aikamatkustajan matkaan ajassa taaksepäin.
Tässä on yksi yksinkertainen esimerkki tästä ilmiöstä: Vuonna 2020 Jim rakentaa ullakoltaan löytämistään suunnitelmista aikakoneen ja päättää matkustaa ajassa taaksepäin nähdäkseen nuoremman itsensä. Jim siis matkustaa takaisin vuoteen 1990 ja löytää nuoremman itsensä. Jim antaa nuoremmalle itselleen aikakoneen piirustukset. Hänen nuorempi minänsä pitää ajatusta aikamatkustamisesta naurettavana ja tunkee suunnitelmat ullakolleen. Sitten vuonna 2020 Jim löytää nuo piirustukset ja rakentaa aikakoneensa.
Selkeästi se, että Jim voi lähteä aikamatkaseikkailuunsa, on riippuvainen siitä, että Jim ylipäätään lähtee seikkailuun. Jimin toiminta tai jopa pelkkä hänen läsnäolonsa perillä on voinut jotenkin vaikuttaa hänen nuorempaan minäänsä tavalla, joka johtaa hänen matkaansa ajassa taaksepäin. Vielä tarkemmin sanottuna näyttää siltä, että jokainen matka menneisyyteen olisi jollain tavalla vuorovaikutuksessa ihmisten, esineiden tai hiukkasten kanssa, jotka lopulta siirtyvät menneisyydestä tulevaisuuteen, mikä tarkoittaa, että kaikki aikamatkat johtavat kausaaliseen silmukkaan. Potentiaalinen muutos, joka jollakin tavalla aiheuttaa tapahtumaketjun, joka vaikuttaa matkalle menneisyyteen, joka tuotti alkuperäisen muutoksen, näyttää olevan aito.
Mutta pelkkä potentiaali aiheuttaa tapahtuma ei edellytä, että tapahtuma tapahtuu. Monton väittää keksineensä hypoteettisen tilanteen, johon liittyy aikamatkailu ilman kausaalisilmukoita. Hän kuvaa maailmankaikkeutta, joka on jaettu kahteen alueeseen, jotka sisältävät vain A-, B- ja C-hiukkasia. (Ks. kuva 1.) Alue 1 sisältää vain A- ja C-hiukkasia sekä alueen näiden kahden alueen rajalle asti. Alue 2 sisältää vain B- ja C-hiukkasia ja alueen samaan rajaan asti. Voimakenttä estää B-hiukkasia ylittämästä rajaa alueelle 1. C-hiukkaset eivät ole koskaan vuorovaikutuksessa A- tai B-hiukkasten kanssa, ja ne liikkuvat vapaasti alueiden 1 ja 2 välillä. Kun A-hiukkanen ylittää rajan, hiukkanen muuttuu välittömästi B-hiukkaseksi.
Katsotaan nyt seuraavaa skenaariota: A-hiukkanen liikkuu kohti rajaa. Samalla hetkellä, kun hiukkanen saavuttaa rajan, se muuttuu B-hiukkaseksi ja alkaa myös matkustaa ajassa taaksepäin. Matkustaessaan ajassa A-hiukkanen seuraa rajaa, jolloin A-hiukkanen ei pääse vuorovaikutukseen minkään muun hiukkasen kanssa. Tämän esimerkin alkuehtojen perusteella tämä A-hiukkanen on ainoa hiukkanen, joka voi päästä rajalle. Heti kun hiukkanen lakkaa aikamatkustamasta, A-hiukkanen siirtyy alueelle 2 (Monton 2009, 60).
Kuvio 3: Montonin esimerkki
Näyttäisi siltä, että A-hiukkanen pystyy aikamatkustamaan vuorovaikuttamatta minkään kummankaan alueen hiukkasen kanssa, mukaan lukien nuorempi itsensä. Kun se on aikamatkalla menneisyyteen ja sen jälkeen, kun se on lopettanut aikamatkansa, raja estää tätä hiukkasta vuorovaikuttamasta menneisyyteen lähdön kanssa. Tämä tarkoittaa, että hiukkanen A on onnistuneesti tehnyt aikamatkan ilman, että se on joutunut kausaalisilmukkaan, koska A:n hiukkasen aikamatkustus ei olisi voinut aiheuttaa sitä, että juuri tämä hiukkanen olisi aloittanut aikamatkansa.
Yleisesti ottaen erityisesti realistisemmissa tilanteissa, tilanteissa, joiden fysiikka muistuttaa enemmän omaa fysiikkaamme, ajatus aikamatkustuksesta menneisyyteen ilman, että kausaalisilmukoita esiintyy jossakin muodossa, vaikuttaa epätodennäköiseltä. Montonin nokkelan skenaarion synnyttämiseksi tarvitaan äärimmäisen huolellinen ja täsmällinen kuvaus.
Do Causal Loops Require Time Travel?
Kausaalisilmukka sisältää aina taaksepäin suuntautuvaa kausaalisuutta yksinkertaisesti siksi, että jossain vaiheessa yhden silmukan tapahtumista on oltava syy aikaisempaan tapahtumaan. Tämä ei kuitenkaan todista, että kaikki kausaalisilmukat sisältävät aikamatkailua. Sisältyykö taaksepäin suuntautuvaan kausaatioon aina aikamatkailu?
Joskus ei ja joskus kyllä. Universumissa, jossa esineet voivat vaikuttaa vain sellaiseen esineeseen, joka on olemassa samaan aikaan kuin se itse, aikamatkailu olisi välttämätöntä, jotta voitaisiin vaikuttaa aikaisempaan aikaan oleviin esineisiin. Jotta objekti voisi vaikuttaa objekteihin, jotka ovat eri ajassa kuin objektin oma aika, kyseisen objektin pitäisi matkustaa eri aikaan ja tuolloin vaikuttaa toiseen objektiin. Jos maailmankaikkeus kuitenkin sallisi objektien vaikuttaa toisiinsa eri ajankohdista käsin, aikamatkailu ei olisi enää tarpeen. Koska taaksepäin suuntautuva kausaatio ei vaadi aikamatkailua, eivät myöskään kausaalisilmukat edellytä sitä.
Kausaalisilmukat ja moniulotteinen aika
Aikarakenne, jossa aikajänteet haarautuvat – jota joskus kutsutaan moniulotteiseksi ajaksi – poistaa suurimman osan kausaalisilmukoiden mielenkiintoisista piirteistä. (Katso verkkosivujemme moniulotteinen aika -teemasivu.) Itse asiassa se otetaan joskus käyttöön, jotta kausaalisilmukat jäisivät pois (Deutsch 1991, Deutsch ja Lockwood 1994). Moniulotteisessa ajassa aikamatkustaminen aiheuttaa aikajanojen jakautumisen, joten tapahtuma ei voi aiheuttaa tapahtumaa oman menneisyyshaaransa varrella. Tämä ”purkaa” silmukat, ja jäljelle jää vain sarja jakautuneita kausaaliketjuja. Yksi seuraus tästä on se, että jos moniulotteinen aika olisi totta, vastaus kysymykseen siitä, liittyykö aikamatkustamiseen menneisyyteen aina kausaalisilmukka, olisi selvä ei. Aikamatkustaja luo haaroja silmukoiden sijaan.
Kausaalisilmukat ja fysiikka
Jotta voisimme esitellä joitakin teoreettisia kausaalisilmukoita fysiikan kontekstissa, tarkastellaan ajatusta ajan kaltaisesta käyrästä. Ajan kaltainen käyrä on objektin polku aika-avaruuden läpi, jossa objekti pysyy paikallisesti ajassa eteenpäin niin, että jokaisen ajanjakson välillä on ajan kaltaisia yhteyksiä. Kausaalisilmukka syntyy, kun objektin ajan kaltainen käyrä kiertyy takaisin itseensä.
Yksi tapa esitellä kausaalisilmukka on ajatus siitä, että maailmankaikkeudella on rullattu aika-avaruus (Gott 2001, 82-85). Paras analogia tälle ajatukselle on sylinteri, jossa avaruuden muodostavat ulottuvuudet ovat sylinterin akseleita. Tämä rakenne mahdollistaa sen, että kohteen ajan kaltainen käyrä kiertää sylinterin ympäri ja kohtaa itsensä.
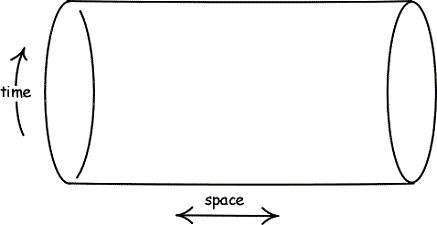
Kuvio 4: Kaareva aika-avaruus
Matoluukkupohjainen aikamatkailu mahdollistaa myös suljetut ajan kaltaiset käyrät, ks. verkkosivujemme Relativiteetti ja aikamatkailu -teemasivua.
Fysiikka aiheuttaa joitain vakavia ongelmia dzinnien mahdollisuuden kannalta. Termodynamiikan toisen lain mukaan entropia (tai epäjärjestys) kasvaa aina ajan myötä. Tarkastellaan esimerkiksi Timeriderin kaulakorua. Termodynamiikan mukaan normaalitilanteessa kaulakorun entropia kasvaisi siitä hetkestä, kun Claire varastaa kaulakorun, siihen hetkeen, kun kaulakoru siirtyy Swannille, ja siihen asti, kunnes Swann matkustaa ajassa taaksepäin. Useimmissa aikamatkustusta koskevissa käsityksissä esineiden tila ei muutu, kun ne matkustavat ajassa taaksepäin. Koska kaulakorun entropian pitäisi kuitenkin juuri ennen Swannin aikamatkan alkua olla yhtä suuri kuin Swannin saapuessa menneisyyteen, tämä olisi ristiriitaista. Ristiriita syntyy, koska kaulakorun entropia juuri ennen Swannin lähtöä on sekä yhtä suuri että suurempi kuin entropia, kun Swann saapuu menneisyyteen. Tämä ristiriita tarkoittaa sitä, että jotta dzinnit voisivat olla olemassa, aikamatkustusmalleissa on jollakin tavalla otettava huomioon entropian pienentäminen sen palatessa menneisyyteen (Gott 2001, 23).
Viimeinen mielenkiintoinen sovellus kausaalisilmukoista fysiikassa on hypoteesi, jonka mukaan maailmankaikkeus sai alkunsa pikemminkin aika-avaruusajan ”donitsina”, josta muu maailmankaikkeus haarautui sen sijaan, että se olisi saanut alkunsa alkuräjähdyksestä. Tämän teorian kirjoittajat J. Richard Gott ja Li-Xin Li (Gott 2001, 186-199) muotoilivat teorian Einsteinin kenttäyhtälöiden vaihtoehtoisen ratkaisun perusteella. Aika-avaruuden donitsi on pohjimmiltaan kausaalisilmukka, jonka ympärillä on sekä suljettuja että avoimia polkuja. Jotkin polut aika-avaruuden läpi ovat siis olemassa silmukkana, mutta on muitakin, jotka haarautuvat ja muodostavat muun maailmankaikkeuden ja sen sisällön (vrt. Meyer 2012, 259).
Johtopäätökset
Palaamme takaisin avausesimerkkiin tuosta moraalisesti epäselvästä termitehtävästä, katsokaamme sitä tarkemmin. Kuten olet ehkä arvannut tämän keskustelun loppuosasta, vaikka voimme analysoida joitakin tämän tarinan näkökohtia onnistuneesti, monet mielenkiintoiset kysymykset ovat vielä avoinna. Esimerkiksi, plagioitko siten, kun toimitit tutkielman? Et koskaan istunut alas ja kirjoittanut paperia, mutta et myöskään kopioinut tai edes tukeutunut kenenkään työhön! Toisena esimerkkinä, ovatko paperin sisältämät ajatukset dzinniä? Onko USB-asemalla oleva digitaalinen tieto jinni? Onko USB-asema itsessään jinni? Onko tarina sopusoinnussa termodynamiikan kanssa? Mikään tarinassa ei viittaa siihen, että entropia ei jotenkin kasvaisi, kun USB-asema lojui housuissasi viikon ajan. Näistä avoimista kysymyksistä huolimatta emme ole kohdanneet mitään kausaalisilmukoihin liittyvää luontaista paradoksia.
Viitteet ja lisälukemista
Arntzenius, Frank ja Maudlin, Tim. ”Aikamatkailu ja moderni fysiikka”. The Stanford Encyclopedia of Philosophy (Winter 2013 Edition), Edward N. Zalta (toim.), <http://plato.stanford.edu/archives/win2013/entries/time-travel-phys/>.
Dear, William. (ohjaaja). Timerider: Lynn Swannin seikkailut . USA: Zoomo Productions, 1982.
Deutsch, David. ’Kvanttimekaniikka lähellä suljettuja aikaviivoja’. Physical Review D 44 (1991): 3197-3217.
Deutsch, David ja Lockwood, Michael. ’The Quantum Physics of Time Travel.’ (Aikamatkustuksen kvanttifysiikka). Scientific American 270 (1990): 68-74.
Gott, J. Richard. Aikamatkailu Einsteinin maailmankaikkeudessa. Boston: Houghton-Mifflin, 2001.
McCall, Storrs. ”Ratkaisematon ongelma”. Analysis 70 (2010): 647-648.
Mellor, D. H. Real Time. Lontoo: Routledge, 1998.
Meyer, Ulrich. ”Kausaalisilmukoiden selittäminen”. Analysis 72 (2012): 259-264.
Monton, Bradley. ”Aikamatkailu ilman kausaalisilmukoita”. The Philosophical Quarterly 59 (2009): 54-67.
Sivukrediitit löytyvät sivulta ”Topics-Page Credits”.