Standardikaava 3×3-matriisin determinantin löytämiseksi on pienempien 2×2-matriisin determinanttiongelmien jako, jotka ovat hyvin helppoja käsitellä. Jos tarvitset kertausta, katso toinen oppituntini 2×2-matriisin determinantin löytämisestä. Oletetaan, että meille annetaan neliömatriisi A, jossa,
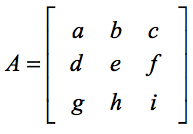
Matriisin A determinantti saadaan laskettua
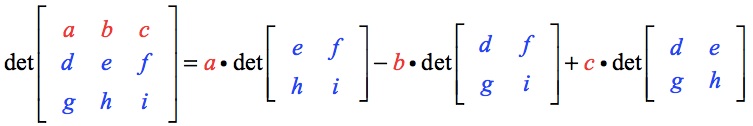
Tässä ovat keskeiset kohdat:
- Huomaa, että ylimmän rivin alkiot, nimittäin a,-, b- ja c-alkio, toimivat vastaavaan 2-by-2 -matriisiin skalaarikertoimina.
- Skalaari a kerrotaan 2×2-matriisiin, joka koostuu ylijääneistä elementeistä, jotka syntyvät, kun a:n kautta kulkevat pysty- ja vaakasuorat viivasegmentit piirretään.
- Skalaarikertojien b ja c 2×2-matriisien rakentamiseen sovelletaan samaa prosessia.
3 x 3 -matriisin determinantti (animoitu)

Esimerkkejä siitä, miten löydetään 3 × 3 -matriisin determinantti
Esimerkki 1: Etsi alla olevan 3×3-matriisin determinantti.
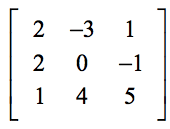
Oheinen asetelma auttaa sinua löytämään vastaavuuden kaavan yleisten alkioiden ja varsinaisen ongelman alkioiden välillä.
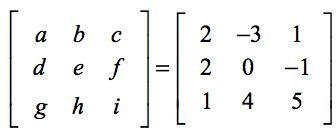
Käytetään kaavaa,


Esimerkki 2: Arvioidaan allaolevan 3×3-koossa olevan 3×3-matriisin determinantti.
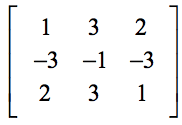
Ole hyvin varovainen, kun korvaat arvot kaavan oikeisiin paikkoihin. Yleisiä virheitä syntyy, kun oppilaat tulevat huolimattomiksi arvojen korvaamisen alkuvaiheessa.
Varmista lisäksi kaikessa rauhassa, että myös aritmeettinen laskutoimituksesi on oikein. Muuten yksikin virhe jossain kohtaa laskutoimitusta tuottaa lopulta väärän vastauksen.
Jos,
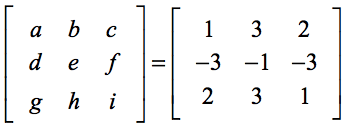
laskutoimituksemme determinantista tulee…

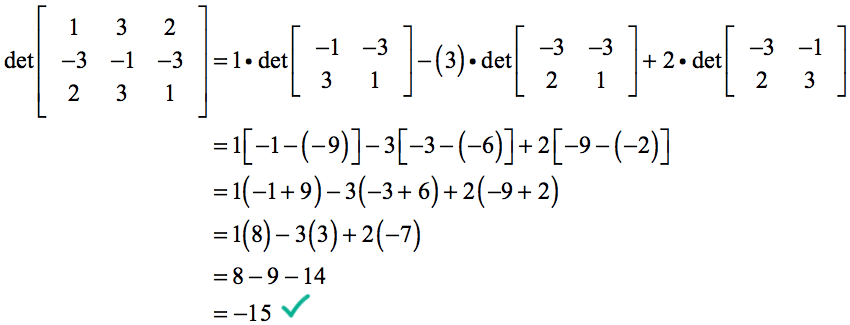
Esimerkki 3: Ratkaise allaolevan 3×3-koossa olevan 3×3-taulukon determinantti.
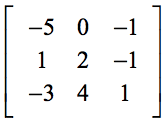
Nollan (0) esiintymisen ensimmäisellä rivillä pitäisi helpottaa laskutoimitustamme huomattavasti. Muista, että ensimmäisen rivin elementit toimivat skalaarikertoimina. Siksi nolla kerrottuna millä tahansa johtaa koko lausekkeen katoamiseen.