Cero es el número entero denotado como 0 que, cuando se utiliza como número de conteo, significa que no hay objetos presentes. Es el único número entero (y, de hecho, el único número real) que no es ni negativo ni positivo. Un número que no es cero se dice que es distinto de cero. Una raíz de una función 
también se conoce a veces como «un cero de 
«.
El segmento de Schoolhouse Rock «My Hero, Zero» ensalza las virtudes del cero con alabanzas como: «My hero, zero Such a funny little hero But till you came along We counted on our fingers and toes Now you’re here to stay And nobody really knows How wonderful you are Why we could never reach a star Without you, zero, my hero How wonderful you are.»
Cero se toma comúnmente para tener la factorización 
(por ejemplo, en el comando FactorInteger de Wolfram Language). Por otra parte, los divisores y la función divisora 
se toman generalmente como indefinidos, ya que por convención, 
(es decir, 
divide a 0) para cada 
excepto el cero.
Debido a que el número de permutaciones de elementos 0 es 1, 
(factorial cero) se define como 1 (Wells 1986, p. 31). Esta definición es útil para expresar muchas identidades matemáticas en forma simple.
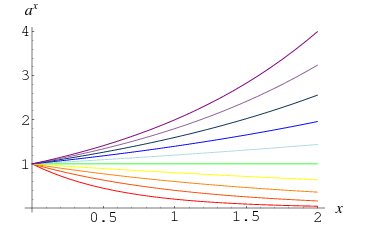
Un número distinto de 0 llevado a la potencia 0 se define como 1, lo que se deduce del límite
 |
(1)
|
Este hecho queda ilustrado por la convergencia de las curvas en 
en el gráfico anterior, que muestra 
para 
, 0.4, …, 2.0. También se puede ver de forma más intuitiva observando que al tomar repetidamente la raíz cuadrada de un número 
se obtienen números cada vez más pequeños que se acercan a uno por arriba, mientras que al hacer lo mismo con un número entre 0 y 1 se obtienen números cada vez más grandes que se acercan a uno por abajo. Para 
raíces cuadradas, la potencia total tomada es 
, que se acerca a 0 a medida que 
es grande, dando 
en el límite en que 
es grande.
mismo es indefinido. La falta de un significado bien definido para esta cantidad se deriva de los hechos mutuamente contradictorios que 
es siempre 1, por lo que 
debe ser igual a 1, pero 
es siempre 0 (para 
), por lo que 
debe ser igual a 0. Se podría argumentar que 
es una definición natural ya que
 |
(2)
|
Sin embargo, el límite no existe para valores complejos generales de 
. Por lo tanto, la elección de la definición para 
suele definirse como indeterminada.
Sin embargo, la definición de 
permite expresar algunas fórmulas de forma sencilla (Knuth 1992; Knuth 1997, p. 57), un ejemplo de lo cual es la hermosa fórmula analítica para la integral de la función sinc generalizada
 |
(3)
|
dada por Kogan (cf. Espinosa y Moll 2000), donde 
, 
, y 
es la función suelo.
El teorema de Richardson es un resultado fundamental en la teoría de decidibilidad que establece que la determinación de si incluso las expresiones simples son idénticamente iguales a cero es indecidible en principio, y mucho menos en la práctica.
La siguiente tabla da los primeros números 
tales que la expansión decimal de 
no contiene ceros para 
pequeños (un problema que se parece a la pregunta de Gelfand.) El mayor 
conocido para el que 
no contiene ceros es 86 (Madachy 1979), sin ningún otro 
(M. Cook, com. pers, Sep. 26, 1997 y Mar. 16, 1998), mejorando el límite 
obtenido por Beeler y Gosper (1972). Los valores 
tales que las posiciones del cero más a la derecha en 
aumentan son 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, … (OEIS A031140). Las posiciones en las que aparecen los ceros de la derecha son 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, … (OEIS A031141). El cero más a la derecha de 
se encuentra en el decimal 217, el más lejano para las potencias hasta 
.
 |
Sloane |  tal que  no contiene 0s |
| 2 | A007377 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, … |
| 3 | A030700 | 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, … |
| 4 | A030701 | 1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, … |
| 5 | A008839 | 1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, … |
| 6 | A030702 | 1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, … |
| 7 | A030703 | 1, 2, 3, 6, 7, 10, 11, 19, 35 |
| 8 | A030704 | 1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27 |
| 9 | A030705 | 1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34 |
| 11 | A030706 | 1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, … |
Si bien no se ha demostrado que los números enumerados anteriormente sean los únicos sin ceros para una base determinada, la probabilidad de que existan otros adicionales es infinitamente pequeña. Bajo este supuesto, la secuencia de mayores 
tal que 
no contiene ceros para 
, 3, … viene dada entonces por 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, … (OEIS A020665).