Nula

Nula je celé číslo označené 0, které při použití jako počítací číslo znamená, že nejsou přítomny žádné objekty. Je to jediné celé číslo (a vlastně jediné reálné číslo), které není ani záporné, ani kladné. O čísle, které není nulové, se říká, že je nenulové. Kořen funkce se také někdy označuje jako „nula .“

Segment Schoolhouse Rock „My Hero, Zero“ vychvaluje přednosti nuly takovými chvalozpěvy: „Můj hrdino, nulo Takový legrační malý hrdina Ale dokud jsi nepřišel, počítali jsme na prstech rukou a nohou Teď jsi tady, abys zůstal A nikdo vlastně neví, jak jsi úžasný Proč bychom nikdy nedosáhli hvězdy Bez tebe, nulo, můj hrdino, jak jsi úžasný.“

Nula se běžně považuje za faktorizaci (např, v příkazu FactorInteger jazyka Wolfram). Naproti tomu dělitelé a funkce dělitele se obecně berou jako nedefinované, protože podle konvence (tj. dělí 0) pro každý kromě nuly.“

Protože počet permutací prvků 0 je 1, (faktoriál nuly) je definován jako 1 (Wells 1986, s. 31). Tato definice je užitečná při vyjadřování mnoha matematických identit v jednoduché formě.

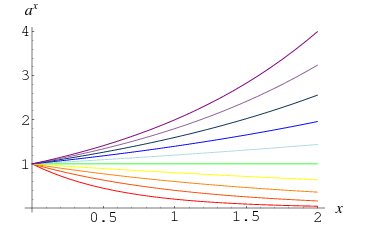
Číslo jiné než 0 vzaté na mocninu 0 je definovánojako 1, což vyplývá z limity

Tuto skutečnost ilustruje konvergence křivek u ve výše uvedeném grafu, který ukazuje pro , 0.4, …, 2.0. Intuitivněji to lze vidět také tak, že si všimneme, že opakovaným odmocňováním čísla získáme menší a menší čísla, která se shora blíží k jedné, zatímco když totéž provedeme s číslem mezi 0 a 1, získáme větší a větší čísla, která se zdola blíží k jedné. Pro odmocniny je celková odebraná mocnina , která se s velikostí čísla blíží k nule a dává v limitě, že je velké.

samo o sobě je neurčité. Neexistence dobře definovaného významu této veličiny vyplývá ze vzájemně si odporujících skutečností, že je vždy 1, takže by se mělo rovnat 1, ale je vždy 0 (pro ), takže by se mělo rovnat nule. Lze namítnout, že je přirozená definice, protože

Pro obecné komplexní hodnoty však limita neexistuje. Proto je volba definice pro obvykle definována jako neurčitá.

Definice však umožňuje některé vzorce vyjádřit jednoduše (Knuth 1992; Knuth 1997, str. 57), příkladem je krásný analytický vzorec pro integrál zobecněné funkce sinc

podaný Koganem (srov. Espinosa a Moll 2000), kde , a je funkce floor.

Richardsonova věta je základním výsledkem teorie rozhodnutelnosti, který stanoví, že určení toho, zda jsou i jednoduché výrazy identicky rovny nule, je nerozhodnutelné v principu, natož v praxi.

Následující tabulka uvádí několik prvních čísel takových, že desetinný rozklad neobsahuje nuly pro malé (problém, který se podobá Gelfandově otázce.) Největší známé , pro které neobsahuje nuly, je 86 (Madachy 1979), přičemž žádné jiné (M. Cook, pers. comm..), 26. 9. 1997 a 16. 3. 1998), což zlepšuje hranici , kterou získali Beeler a Gosper (1972). Hodnoty takové, že pozice nejpravější nuly v roste, jsou 10, 20, 30, 40, 46, 68, 93, 95, 129, 176, 229, 700, 1757, 1958, 7931, 57356, 269518, …. (OEIS A031140). Pozice, na kterých se vyskytují nuly nejvíce vpravo, jsou 2, 5, 8, 11, 12, 13, 14, 23, 36, 38, 54, 57, 59, 93, 115, 119, 120, 121, 136, 138, 164, …. (OEIS A031141). Nejpravější nula se vyskytuje na 217. desetinném místě, což je nejdále pro mocniny do .

	Sloane	takové, že neobsahuje žádné nuly
2	A007377	1, 2, 3, 4, 5, 6, 7, 8, 9, 13, 14, 15, 16, 18, 19, 24, 25, 27, 28, …
3	A030700	1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 19, 23, 24, 26, 27, 28, …
4	A030701	1, 2, 3, 4, 7, 8, 9, 12, 14, 16, 17, 18, 36, 38, 43, …
5	A008839	1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 17, 18, 30, 33, 58, …
6	A030702	1, 2, 3, 4, 5, 6, 7, 8, 12, 17, 24, 29, 44, …
7	A030703	1, 2, 3, 6, 7, 10, 11, 19, 35
8	A030704	1, 2, 3, 5, 6, 8, 9, 11, 12, 13, 17, 24, 27
9	A030705	1, 2, 3, 4, 6, 7, 12, 13, 14, 17, 34
11	A030706	1, 2, 3, 4, 6, 7, 8, 9, 12, 13, 14, 15, 16, 18, 41, ….

Ačkoli nebylo prokázáno, že výše uvedená čísla jsou pro daný základ jediná bez nul, pravděpodobnost, že existují nějaké další, je mizivě malá. Za tohoto předpokladu je pak posloupnost největších takových, že neobsahuje žádné nuly pro , 3, … dána 86, 68, 43, 58, 44, 35, 27, 34, 0, 41, …. (OEIS A020665).