Eine wichtige Frage ist, wie die Primzahlen unter den ganzen Zahlen verteilt sind. Die Antwort ist, in wenigen Worten, ziemlich zufällig, wenn man bestimmte statistische Grundlagen berücksichtigt…
 Bill Casselman
Bill Casselman
Universität von British Columbia, Vancouver, Kanada
Email Bill Casselman
| |
|
Einleitung
Vor vielen Jahren wurde vermutet, dass es eine unendliche Anzahl von Primzahlpaaren $p$, $q$ mit $q = p+2$ gibt. In letzter Zeit hat es einige (und berühmte) Fortschritte bei diesem Problem gegeben. Ich werde wenig über die jüngsten Fortschritte sagen, sondern stattdessen erörtern, was wir über solche Paare erwarten – und nicht, was wir wissen. Nichts von dem, was ich sagen werde, ist neu, und ich habe in gewissem Maße nur das weiter ausgeführt, was Andrew Granville in seiner jüngsten Erläuterung zu den jüngsten Fortschritten sagt.
Wie viele Primzahlen erwarten wir?
Eine Primzahl ist eine positive ganze Zahl, die keine Teiler außer sich selbst und $1$ hat. Die Definition ist einfach, aber sobald man anfängt, die Bedeutung von Primzahlen zu erforschen, stellt man fest, dass sie ein sehr subtiles Verhalten aufweisen. Eine wichtige Frage ist, wie die Primzahlen unter den ganzen Zahlen verteilt sind. Die Antwort ist, in wenigen Worten, ziemlich zufällig, wenn man bestimmte statistische Grundlagen berücksichtigt. Was meine ich damit?
Nun, hier ist ein quadratisches Feld, das alle Primzahlen bis $400$ abbildet:

Es gibt einige Muster in diesem Feld, von denen ich einige später kommentieren werde. Die meisten dieser Muster, die Sie wahrnehmen, sind auf ein Artefakt der Anzeige zurückzuführen. Zum Beispiel ist jede zweite Spalte im Wesentlichen leer, und das liegt daran, dass die einzige gerade Primzahl $2$ ist. Auch jede fünfte Spalte ist im Wesentlichen leer. Interessanter sind die Zwillingsprimzahlpaare (von denen einige nicht so gut sichtbar sind, weil sie sich in zwei Reihen aufteilen, z. B. $59$, $61$), und auch einige Muster, die mit den letzten angezeigten Ziffern zusammenhängen. Diese Muster könnte man als lokale Muster bezeichnen. Es sind keine globalen Muster zu erkennen.
Es wurden viele Anstrengungen unternommen, um extrem effiziente Verfahren zur Erzeugung von Primzahlen zu entwickeln, aber heutzutage benötigt selbst ein sehr einfaches Programm nur wenig Zeit, um große Listen von Primzahlen zu erstellen. Eines der fruchtbarsten Programme erstellt eine große Liste von Primzahlen und berechnet daraus die Funktion $\pi(n)$, die Anzahl der Primzahlen $\le n$.
Eine Sache, für die dies verwendet werden kann, ist, eine grobe Vorstellung von der Häufigkeit der Primzahlen zu bekommen. Es gibt $135$ Primzahlen im Bereich $$:
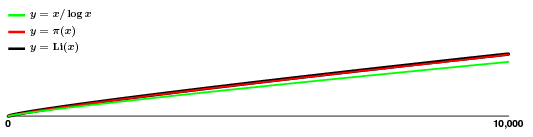
Die Näherung sieht gut aus! Auch wenn $\pi(x)$ ein wenig hin und her springt, scheinbar ohne großes Muster, haben wir eine ziemlich gute Schätzung dafür, was bedeutet, dass wir eine gute Vorstellung davon haben, wie die Primzahlen wachsen, zumindest im Durchschnitt.
Man sollte jedoch bedenken, dass die scheinbare Glätte täuscht. Aus der Nähe betrachtet, sehen die beiden oberen Kurven so aus:

Kommentare?
Heuristische Überlegungen zu Zwillingsprimzahlen
Zwillingsprimzahlen sind ein Paar $p$, $p+2$, die beide Primzahlen sind. In einem der obigen Diagramme sehen wir zum Beispiel die Zwillingsprimzahlen $$ , , , , , , $$
und andere. Es wurde vermutet, dass es unendlich viele von ihnen gibt, aber obwohl es viele empirische Beweise dafür gibt, wurde dies noch nicht bewiesen.
Der vielleicht stärkste Beweis ist eine Formel, die die Anzahl $\pi_{2}(x)$ der Zwillings-Primzahlen $\le x$ bemerkenswert gut approximiert. Ich bin mir über den Ursprung dieser Formel nicht ganz sicher, aber sie erschien erstmals in einem Aufsatz von G. H. Hardy und J. E. Littlewood (selbst ein Paar von Zwillingsprimzahlen) aus dem Jahr 1923. Das Papier enthält mehrere ähnliche Formeln, die alle auf derselben Methode beruhen, mit der sie schon viele Probleme gelöst hatten. Dies war ihre Kreismethode. Ihre Herleitung der Formel für $\pi_{2}(x)$ ist keineswegs streng, aber sie ist sehr überzeugend. In einem Anhang zu Andrew Granvilles Artikel findet sich eine knappe Darstellung.
Aber kurz nach dem Zweiten Weltkrieg schlug Lord Cherwell (Frederick Lindemann) eine elementarere probabilistische (und immer noch nicht strenge) Herleitung vor. Dies führte zu einer Zusammenarbeit mit E. M. Wright und schließlich zu einer posthumen gemeinsamen Veröffentlichung. Dies wird in Abschnitt 22.20 des bekannten Textes von Hardy und Wright erläutert. Eine etwas elementarere Version davon findet sich auch in einem Anhang von Granvilles Artikel (Abschnitt 2.5). Ich folge ihm.
Ausgangspunkt für die plausible Argumentation ist unsere Abschätzung für $\pi(x)$, die Anzahl der Primzahlen kleiner oder gleich $x$. Die Grundidee der Herleitung ist, dass die Primzahlen zu einem guten Teil zufällig verteilt sind. Wir wissen, dass in der Umgebung von $x$ die Dichte der Primzahlen etwa $1/\log x$ beträgt. Wären die Primzahlen zufällig verteilt, dann wäre die Wahrscheinlichkeit, dass zwei beliebige Zahlen in der Nähe von $x$ Primzahlen sind, nur das Produkt der lokalen Wahrscheinlichkeiten, also $1/\log^{2} x$. Das ist natürlich eine fadenscheinige Argumentation, denn wenn $n > 2$ ist die Wahrscheinlichkeit, dass sowohl $n$ als auch $n+1$ Primzahlen sind, $0$, während die Tatsache, dass $p$ eine Primzahl ist, die Wahrscheinlichkeit erhöhen würde, dass $p+2$ eine ist. Ähnliche Überlegungen sind auch wegen der möglichen Teilbarkeit durch andere kleine Primzahlen in der Nachbarschaft von $x$ anzustellen.
Es gibt eine einfache Tatsache in dieser Geschichte. Wenn $q$ eine beliebige Primzahl ist, dann ist die Wahrscheinlichkeit, eine ganze Zahl zufällig zu wählen, die nicht durch $q$ teilbar ist, $1-1/q$. Die Wahrscheinlichkeit, zwei durch $q$ nicht teilbare Zahlen zu wählen, ist also das Produkt $(1 – 1/q)^{2}$. Angenommen $p$ und $p+2$ sind beide Primzahlen, dann ist weder $p$ noch $p+2$ durch $q$ teilbar. Wenn $q = 2$ ist, geschieht dies $1/2$ der Zeit. Ist $q \ne 2$, so ist die Wahrscheinlichkeit, dass $p \not\equiv 0$ und $p \not\equiv -2$ modulo $q$ ist $(1 – 2/q)$. Aufgrund des Chinesischen Remainder-Satzes ist die Teilbarkeit durch zwei Primzahlen ein unabhängiges Ereignis. Wenn also $x$ groß und $Q$ relativ klein ist, ist die Wahrscheinlichkeit, dass ein beliebiges Zahlenpaar $m$ und $n$ in der Nähe von $x$ kein Vielfaches einer Primzahl bis $Q$ ist, $$ { 1\über 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} } \, . $$
Sei $\Gamma_{Q}$ das Verhältnis von diesem zu $\prod_{q \le Q}(1 – 2/q)$: $$ \Gamma_{Q} = { 1\über 2} \cdot \prod_{q \le Q} { (1 – 1/q)^{2} \over (1 – 2/q) } $$ Wir haben $$ { 1 – 2/q \over (1-1/q)^{2} } = { (1 – 1/q)^{2} – 1/q^{2} \over (1 – 1/q)^{2} } = 1 – { 1 \over (q -1)^{2} } \, . $$ Ein Standardkriterium besagt, dass dieses Produkt konvergiert, wenn die Summe $\sum 1/(q-1)^{2}$ konvergiert. Es konvergiert aber, denn der Integraltest sagt uns, dass $\sum 1/n^{2}$ konvergiert. Daher konvergiert dieses Produkt tatsächlich zu einer Zahl $\Pi_{\infty}$ als $Q \rightarrow \infty$. Sei $C_{2}$ seine Inverse. In Abschnitt 2.5 von Granvilles Artikel heißt es, dass es an dieser Stelle intuitiv einleuchtend sein sollte, dass die Anzahl $\pi_{2}(x)$ der Zwillingsprimzahlen $\le x$ durch $$ \Pi_{2}(x) = C_{2} \int_{2}^{\infty} { dx \über \log^{2} x } \$$
Der Text von Hardy und Wright enthält eine sorgfältigere Analyse, die den intuitiven Sprung etwas klarer macht.
Der Wert der Konstante hier wurde vor langer Zeit von J. W. Wrench berechnet und beträgt etwa $1.32032363169373914785562422002911155686525 \ldots $. Hier ist ein Vergleich einiger Werte von $\pi_{2}(x)$ und der Formel im Bereich $$: $$ \matrix{ n & 10.000 & 20.000 & 30.000 & 40.000 & 50.000 \cr \pi_{2}(n) & 205\phantom{.0} & 342 \phantom{.0} & 467 \phantom{.0} & 591 \phantom{.0} & 705 \phantom{.0} & \cr \Pi_{2}(x) & 214,2 & 357,7 & 486,7 & 607,4 & 722,5 \cr } $$ $$ \matrix{ n & 60.000 & 70.000 & 80.000 & 90.000 & 100.000 \cr \pi_{2}(n) & 811 \phantom{.0} & 905 \Phantom{.0} & 1007 \phantom{.0} & 1116 \phantom{.0} & 1224\phantom{.0} \cr \Pi_{2}(x) & 833,3 & 940,9 & 1045,7 & 1148,2 & 1248,7 \cr } $$
Kommentare?
Dicksonsche Vermutung
Doppelte Primzahlen sind ein Spezialfall von etwas viel Allgemeinerem. Man kann fragen, ob es unendlich viele Paare $p$, $p+4$ oder $p$, $p+6$ gibt, die Primzahlen sind? Oder $p$, $p+10$? Der Fall von $p$ und $p+10$ wird sicherlich durch eines der obigen Bilder nahegelegt, auf dem solche Paare leicht zu erkennen sind. Wie wäre es mit einer Art von Dreiergruppen? Nehmen wir an, dass $a_{1}$, $a_{2}$, $\ldots$ , $a_{k}$ eine Reihe von ganzen Zahlen bilden. Kann man erwarten, dass es unendlich viele Mengen $n+a_{1}$, $n+a_{2}$, $\ldots$ , $n+a_{k}$ gibt, die alle prim sind?
Man muss ein bisschen vorsichtig sein. Es gibt keine Primzahlpaare der Form $p$, $p+1$ (nach $p = 2$), weil eine dieser beiden Zahlen durch $2$ teilbar sein muss. Ebenso gibt es nach $p = 3$ keine Primzahlendreier der Form $p$, $p+2$, $p+4$, weil eine dieser Zahlen durch $3$ teilbar sein muss.
Dieses letzte Beispiel sollte aufschlussreich sein. Die Zahl $p+4$ ist dann und nur dann durch $3$ teilbar, wenn $p+1$ durch $3$ teilbar ist. Also teilt $3$ eine der Zahlen $p$, $p+2$, $p+4$ nur dann, wenn sie $p$, $p+1$, $p+2$ teilt. Das ist aber sicher, da das letzte Tripel eindeutig alle Zahlen modulo $3$ abdeckt.
Im Allgemeinen sagt man, dass $p$ ein Hindernis für die Anordnung $(a_{i})$ ist, wenn $p$ immer mindestens eine der Folgen $n+a_{i}$ ($i = 1$, $\ldots$, $k$) teilt. Dies ist dann und nur dann der Fall, wenn die Zahlen $a_{i} \; {\rm mod} \, p$ ganz $Z/p$ ausfüllen.
Dies kann nie geschehen, wenn $p > k$, so dass wir, um zu prüfen, ob irgendein $p$ $(a_{i})$ behindert, nur prüfen müssen, ob die $a_{i}$ $Z/p$ für alle $p \le k$ abdecken. Wir nennen die Anordnung $(a_{i})$ zulässig, wenn sie keine Primzahlhindernisse hat.
Zum Beispiel ist $(1,3,7,9)$ eine zulässige Anordnung, da, wie man leicht prüfen kann, weder $2$ noch $3$ ein Hindernis ist. Mehrere Primzahlfolgen, die in dieses Muster passen, sind in einem der Diagramme oben zu sehen. Andere Beispiele sind (a) beliebige $0$, $2n$; (b) $0$, $4$, $6$; (c) $0$, $2$, $6$.
Es gibt beliebig große zulässige Mengen. In der Tat:
Theorem. Wenn $a_{1}$ bis $a_{k}$ eine beliebige Menge von verschiedenen Primzahlen $> k$ ist, bilden sie eine zulässige Menge.
Warum ist das so? Wenn $p$ eine beliebige Primzahl mit $p> k$ ist, dann haben wir bereits gesehen, dass sie kein Hindernis sein kann. Aber wenn $p k$ ist, dann kann es keine der $a_{i}$ teilen, von denen keine kongruent zu $0$ modulo $p$ sein kann. Die $a_{i}$ füllen also $Z/p$ nicht auf.
Ein Spezialfall einer Vermutung, die ursprünglich von L. E. Dickson aufgestellt wurde, ist, dass, wenn es keine Primzahlhindernisse für $(a_{i})$ gibt, eine unendliche Anzahl von Primzahlfolgen der Form $(n +a_{i})$ existiert.
Was in letzter Zeit passiert ist
Dies ist nicht der Ort, um die ganze Geschichte zu erzählen, die an anderer Stelle ausführlich behandelt wurde. Ich empfehle insbesondere den Quanta-Artikel von Erica Klarreich für eine populäre Darstellung und Granvilles Aufsatz für eine eher technische Darstellung. Ich möchte nur etwas präziser als in Klarreichs Bericht darlegen, was das berühmteste der neuen Ergebnisse ist.
Es geht auf Yitang Zhang zurück. Die einfachste Aussage dessen, was er bewies, ist, dass es eine unendliche Anzahl von Intervallen $[n, n+70.000.000)$ gibt, die mindestens zwei Primzahlen enthalten. Dies ist schwächer als die Zwillingsprimzahlvermutung, aber konzeptionell sehr nahe an ihr. In späteren Arbeiten (von vielen Mathematikern) wurde die Größe der Lücke stark reduziert, aber es gibt vermutlich keine Möglichkeit, sie mit heutigen Methoden auf $2$ zu reduzieren.
Wie von Granville erläutert, ist Zhangs erstes und wohl sein wichtigstes Ergebnis, dass es $k$ mit der Eigenschaft gibt, dass, wenn $a_{1}$, $\ldots$ , $a_{k}$ eine zulässige Menge von $k$ Elementen ist, dann gibt es eine unendliche Anzahl von $n$, so dass $\{ n +a_{i} \}$ mindestens zwei Primzahlen enthält. (In Klarreichs Quanta-Artikel wird die Anordnung als „Kamm“ bezeichnet. Denken Sie daran, dass wir nach Dickson’s Vermutung erwarten würden, dass alle $k$ Primzahlen sind.) Tatsächlich bewies Zhang, dass diese Behauptung für ein bestimmtes $k =3.500.000$ wahr ist, das ein Intervall von $70.000.000$ umspannt. Die mittlerweile berühmte Konsequenz ist, dass es für einige $m \lt 70.000.000$ eine unendliche Anzahl von Primzahlpaaren $p$, $p+m$ gibt.
Weiterlesen
- Lord Cherwell und E. M. Wright, „The frequency of prime patterns“, The Quarterly Journal of Mathematics 11 (1960).
Wer etwas über das Leben von Lord Cherwell, auch bekannt als Frederick Lindemann, weiß, wird über seinen Beitrag zur Zahlentheorie sehr überrascht sein. Die Wikipedia-Biographie deutet nicht alle Gründe für seinen schlechten Ruf als wissenschaftlicher Hauptberater von Churchill während des Zweiten Weltkriegs an.
- L. E. Dickson, „A new extension of Dirichlet’s theorem on prime numbers“, Messenger of Mathematics 33.
Siehe auch den Wikipedia-Eintrag zu Dicksons Vermutung.
- Andrew Granville, „Primzahlen in Intervallen von begrenzter Länge“. Erhältlich auf seiner Homepage.
- G. H. Hardy, Ramanujan, Cambridge University Press.
Abschnitt 2.5 enthält eine ideale Herleitung einer möglichen Formel für $\pi(x)$.
- G. H. Hardy und J. E. Littlewood, „Some problems of ‚Partitio numerorum‘ III: on the expression of a number as a sum of primes“, Acta Mathematica 44 (1923).
- G. H. Hardy and E. M. Wright, The theory of numbers, Oxford Press.
- Erica Klarreich, „Together and alone, closing the prime gap“, Quanta November 19, 2013.
- B. Riemann, „Über die Anzahl der Primzahlen, die kleiner als eine bestimmte Menge sind“. Eine englische Übersetzung dieses Klassikers von David Wilkins ist über einen Link in der Wikipedia verfügbar.
Unter anderem wird darin eine Herleitung der Näherungsformel für $\pi(x)$ skizziert.
- J. W. Wrench, „Evaluation of Artin’s constant and the twin-prime constant“, Mathematics of Computation 76 (1961).
Eine frühe Berechnung von $C_{2}$.
- Listen der Primzahlen bis $1.000.000.000.000$
- Eine Liste der ersten 20.000 Zwillingsprimzahlen.
 Bill Casselman
Bill Casselman
University of British Columbia, Vancouver, Canada
Email Bill Casselman