Die Viertklässlerin Alice fragt: „Wie viele Diagonalen hat das Zehneck?“
Gute Frage, Alice. Aber anstatt dir eine Antwort auf diese Frage zu geben, werde ich dir zeigen, wie du es selbst herausfinden kannst. Und nicht nur das, ich zeige dir auch, wie du die Antwort für jedes Polygon herausfinden kannst, selbst wenn es 20, 50 oder 2000 Seiten hat!
Bereit? Lassen Sie uns mit einem einfachen Beispiel beginnen. Wir nehmen ein Polygon mit 8 Seiten (ein sogenanntes Achteck), etwa so:
Da dieses Polygon acht Seiten hat, hat es auch acht Scheitelpunkte. Es scheint ein wenig überwältigend zu sein, alle Diagonalen herauszufinden, also konzentrieren wir uns auf einen Scheitelpunkt. Wie viele Diagonalen kann man in einem Achteck zeichnen, die alle an einem Scheitelpunkt beginnen?
Die Antwort auf diese Frage ist fünf. Sieh dir das folgende Diagramm an:

In diesem Diagramm habe ich die Diagonale links direkt unter dem obersten Scheitelpunkt gewählt, und ich habe Diagonalen zu jedem Scheitelpunkt gezeichnet, zu dem ich eine Diagonale zeichnen kann. Zu welchen Diagonalen kann ich keine Diagonalen zeichnen? Nun, ich kann keine Diagonale von einem Scheitelpunkt zurück zu sich selbst zeichnen, und ich kann keine Diagonalen zu den beiden Scheitelpunkten neben diesem Scheitelpunkt zeichnen (denn das wären keine Diagonalen, sondern Seiten!).
Es gibt also drei Scheitelpunkte, zu denen ich von diesem Scheitelpunkt aus keine Diagonalen zeichnen kann. Abzüglich der drei Scheitelpunkte, zu denen ich keine Diagonalen ziehen kann, bleiben insgesamt acht Scheitelpunkte übrig, also fünf. Das ist wichtig zu wissen: Ziehe 3 von der Anzahl der Scheitelpunkte ab, und du hast die Anzahl der Diagonalen, die du von jedem Scheitelpunkt aus ziehen kannst.
Aber das ist nur ein Scheitelpunkt! Du könntest doch von jedem Scheitelpunkt aus Diagonalen zeichnen, oder? Genau! Unser Achteck hat acht Scheitelpunkte, also nehmen wir die Anzahl der Diagonalen pro Scheitelpunkt und multiplizieren sie mit der Anzahl der Scheitelpunkte: 5 x 8 = 40.
Man könnte meinen, dass das unsere Antwort ist, aber das ist sie nicht. Warum nicht? Weil wir jede Diagonale zweimal gezählt haben! Jede Diagonale hat zwei Scheitelpunkte, also haben wir sie von einem Ende aus gezählt, und wir haben sie auch vom anderen Ende aus gezählt. Um also die tatsächliche Anzahl der Diagonalen zu erhalten, müssen wir unsere Antwort durch 2 teilen. 40 / 2 = 20. Es gibt zwanzig Diagonalen in einem Achteck.
Lassen Sie uns diese Überlegungen an einem Polygon mit 2000 Seiten ausprobieren. Ich werde jetzt kein 2000er-Eck für dich zeichnen; wir müssen die Argumentation einfach ohne ein Bild ausarbeiten.
- Wähle einen Scheitelpunkt. Wie viele Diagonalen kannst du von diesem Scheitelpunkt aus zeichnen? Antwort: 2000 – 3 = 1997.
- Wie viele Scheitelpunkte insgesamt? Antwort: 2000
- Wie viele Diagonalen von allen Scheitelpunkten aus gezählt? Antwort: 1997 x 2000 = 3.994.000
- Oops! Wir haben jede Diagonale zweimal gezählt! Wie werden wir die Duplikate los? Antwort: 3994000 / 2 = 1.997.000
Ein 2000er-Gon hat also 1.997.000 Diagonalen!
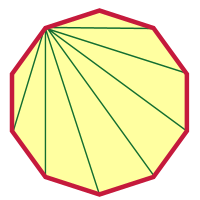
Nach etwas so Verrücktem wie einem 2000er-Gon sollte ein Zehneck nicht mehr so schwierig sein, oder? Ich fange an, und du kannst es von hier aus beenden. Ich habe einen Scheitelpunkt gewählt und von diesem Scheitelpunkt aus Diagonalen gezeichnet.
Wie viele sind es? Konntest du herausfinden, wie viele es sind, ohne dir das Bild anzusehen?
Kannst du es von hier aus herausfinden? Ich hoffe es! Viel Glück, Alice!
Übrigens, es gibt eine Formel, die du verwenden kannst; sie sieht so aus: D = n(n – 3)/2. Aber ehrlich gesagt, erwarte ich nicht, dass meine Schüler sie auswendig lernen. Ich erwarte von ihnen, dass sie sich merken, wie wir das hier begründen. Wenn man die Logik versteht, ist das sogar besser als eine Formel!