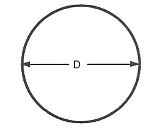
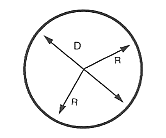
Durchmesser eines Kreises
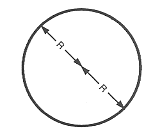
Der Durchmesser eines Kreises oder einer Kugel ist gleich dem 2-fachen des Radius.
$\text „Durchmesser“ = 2 ⋅ \text „Radius“$
Umfang eines Kreises
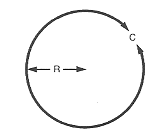
Der Umfang eines Kreises oder einer Kugel ist gleich dem 6,2832-fachen des Radius.
$\text „Umfang“ = 6,2832 ⋅ R$
$C = 2 ⋅ π ⋅ R$
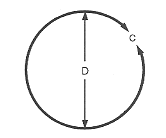
Der Umfang eines Kreises oder einer Kugel ist gleich dem 3,1416-fachen des Durchmessers.
$\text „Umfang“ = 3.1416 ⋅ \text „Durchmesser“$
$C = π ⋅ D$
Radius eines Kreises
Der Radius eines Kreises oder einer Kugel ist gleich dem Durchmesser geteilt durch 2.
$R = D / 2$
Fläche eines Kreises
Die Fläche eines Kreises ist gleich dem Radius des Kreises multipliziert mit dem Radius und dann diese Zahl multipliziert mit 3,1416.
$\text „Fläche“ = R^2 ⋅ π$
$\text „Fläche“ = R ⋅ R ⋅ 3,1416$
Diese Zahl wird in Quadratzoll oder Quadratmillimeter angegeben, je nach dem verwendeten Maßsystem.
Die Fläche eines Kreises ist gleich dem Durchmesser des Kreises multipliziert mit dem Durchmesser und dann diese Zahl multipliziert mit 3,1416 und dann wird diese Summe durch 4 geteilt.
$\text „Fläche“ = D ⋅ D ⋅ 3.1416 / 4$
$\text „Fläche“ = D^2 ⋅ π/ 4$
Fläche eines Zylinders
Diese Zahl wird in Quadratzoll oder Quadratmillimeter angegeben, je nach dem verwendeten Maßsystem.
Der Flächeninhalt eines Zylinders ist gleich 6,2832 ( 2 × π) mal dem Radius des Zylinders, mal der Summe aus Radius und Höhe.
$\text „Fläche“ = 2 ⋅ 3.1416 ⋅ R ⋅ ( R + H )$
$\text „Fläche“ = 2 ⋅ π ⋅ R ⋅ ( R + H )$
Diese Zahl wird in Quadratzoll oder Quadratmillimeter angegeben, je nach dem verwendeten Maßsystem.
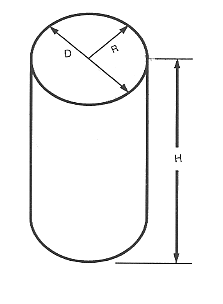
Volumen des Zylinders
Das Volumen des Zylinders ist gleich dem Radius des Zylinders, multipliziert mit dem Radius, und diese Zahl multipliziert mit 3,1416, dann wird diese Zahl mit der Länge des Zylinders multipliziert.
$\text „Volumen“ = 3.1416 ⋅ R ⋅ R ⋅ H$
$\text „Volumen“ = π ⋅ R^2 ⋅ H$
Diese Zahl wird in Kubikzoll oder Kubikmillimetern angegeben, je nach dem verwendeten Maßsystem.
Fläche einer Kugel
Die Fläche einer Kugel ist gleich dem Quadrat des Radius der Kugel multipliziert mit 12,566 ( 4 × π) oder Pi mal dem Durchmesser zum Quadrat ( π × D × D ).
$“Fläche“ = 12.566 ⋅ R ⋅ R$
$\text „Fläche“ = 4 ⋅ π ⋅ R^2$
$\text „Fläche“ = π ⋅ D^2$
Diese Zahl wird in Quadratzoll oder Quadratmillimeter angegeben, je nach dem verwendeten Maßsystem.
Volumen einer Kugel
Das Volumen einer Kugel ist gleich dem Radius der Kugel, multipliziert mit dem Radius wiederum. Dann wird diese Zahl noch einmal mit dem Radius multipliziert. Dann wird diese Zahl mit 12.566. multipliziert und das Ergebnis durch 3 dividiert.
$\text „Volumen“ = 12.566 ⋅ R ⋅ R ⋅ R / 3$
$\text „Volumen“ = 4 ⋅ π ⋅ R ⋅ R ⋅ R / 3$
$\text „Kugelvolumen“ = 4/3 ⋅ π ⋅ r^3 = ( π ⋅ d^3)/6$
Diese Zahl wird in Kubikzoll oder Kubikmillimetern angegeben, je nach dem verwendeten Maßsystem.