Diferitele tipuri de regulatoare sunt utilizate pentru a îmbunătăți performanța sistemelor de control. În acest capitol, vom discuta despre regulatorii de bază, cum ar fi regulatorii proporționali, derivativi și integrali.
Regulator proporțional
Regulatorul proporțional produce o ieșire, care este proporțională cu semnalul de eroare.
$$u(t) \propto e(t) $$
$$\Săgeata din dreapta u(t)=K_P e(t)$$
Aplică transformarea Laplace pe ambele părți –
$$U(s)=K_P E(s)$$
$$\frac{U(s)}{E(s)}=K_P$$$
În consecință, funcția de transfer a regulatorului proporțional este $K_P$.
Unde unde,
U(s) este transformata Laplace a semnalului de acționare u(t)
E(s) este transformata Laplace a semnalului de eroare e(t)
KP este constanta de proporționalitate
Diagrama bloc a sistemului de control în buclă închisă cu reacție negativă unitară împreună cu regulatorul proporțional este prezentată în figura următoare.
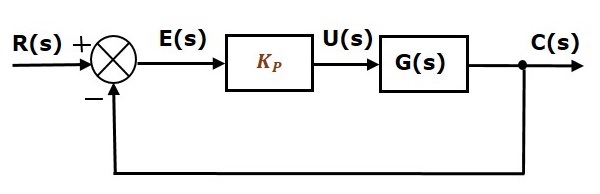
Controlerul proporțional este utilizat pentru a modifica răspunsul tranzitoriu în funcție de cerințe.
Controlerul derivat
Controlerul derivat produce o ieșire, care este derivata semnalului de eroare.
$$u(t)=K_D \frac{\text{d}e(t)}{\text{d}t}$$$
Aplicați transformata Laplace pe ambele părți.
$$U(s)=K_D sE(s)$$
$$\frac{U(s)}{E(s)}=K_D s$$$
Prin urmare, funcția de transfer a regulatorului derivativ este $K_D s$.
Unde, $K_D$ este constanta derivativă.
Diagrama bloc a sistemului de control în buclă închisă cu reacție negativă unitară împreună cu regulatorul derivativ este prezentată în figura următoare.
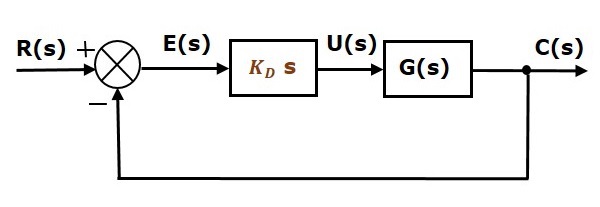
Controlerul derivativ este utilizat pentru a transforma sistemul de control instabil într-unul stabil.
Controlerul integral
Controlerul integral produce o ieșire, care este integrală a semnalului de eroare.
$$u(t)=K_I \int e(t) dt$$$
Aplică transformata Laplace pe ambele părți –
$$U(s)=\frac{K_I E(s)}{s}$$
$$\frac{U(s)}{E(s)}=\frac{K_I}{s}$$$
Deci, funcția de transfer a regulatorului integral este $\frac{K_I}{s}$.
Unde, $K_I$ este constanta integrală.
Diagrama bloc a sistemului de control în buclă închisă cu reacție negativă unitară împreună cu controlerul integral este prezentată în figura următoare.
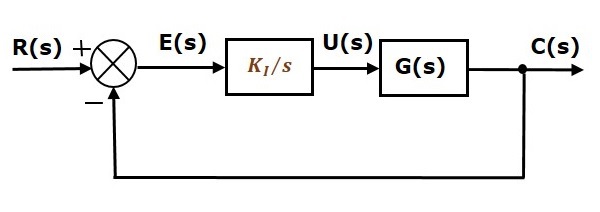
Controlerul integral este utilizat pentru a diminua eroarea în regim staționar.
Să discutăm acum despre combinația de controlere de bază.
Controlerul proporțional derivativ (PD)
Controlerul proporțional derivativ produce o ieșire, care este combinația ieșirilor controlorilor proporțional și derivativ.
$$u(t)=K_P e(t)+K_D \frac{\text{d}e(t)}{\text{d}t}$$$
Aplică transformarea Laplace pe ambele părți –
$$U(s)=(K_P+K_D s)E(s)$$
$$\frac{U(s)}{E(s)}=K_P+K_D s$$$
Deci, funcția de transfer a regulatorului proporțional derivativ este $K_P + K_D s$.
Diagrama bloc a sistemului de control în buclă închisă cu reacție negativă unitară împreună cu regulatorul derivativ proporțional este prezentată în figura următoare.
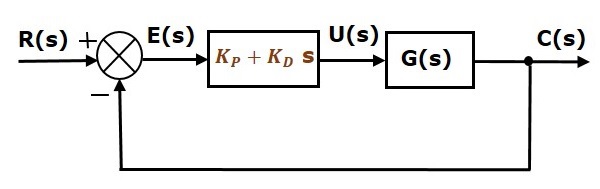
Controlerul derivativ proporțional este utilizat pentru a îmbunătăți stabilitatea sistemului de control fără a afecta eroarea în regim staționar.
Controlerul proporțional integral (PI)
Controlerul proporțional integral produce o ieșire, care este combinația ieșirilor controlorilor proporțional și integral.
$$u(t)=K_P e(t)+K_I \int e(t) dt$$$
Aplică transformata Laplace pe ambele părți –
$$U(s)=\left(K_P+\frac{K_I}{s} \right )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}$$
Deci, funcția de transfer a regulatorului integral proporțional este $K_P + \frac{K_I} {s}$.
Diagrama bloc a sistemului de control în buclă închisă cu reacție negativă unitară împreună cu controlerul integral proporțional este prezentată în figura următoare.
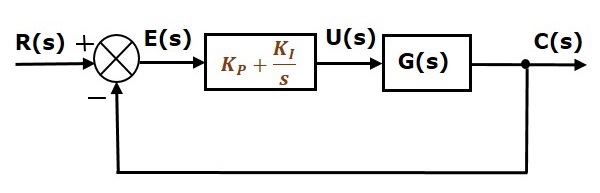
Controlerul integral proporțional este utilizat pentru a diminua eroarea în regim staționar fără a afecta stabilitatea sistemului de control.
Controlerul proporțional integral derivativ (PID)
Controlerul proporțional integral derivativ produce o ieșire, care este combinația ieșirilor controlorilor proporțional, integral și derivativ.
$$u(t)=K_P e(t)+K_I \int e(t) dt+K_D \frac{\text{d}e(t)}{\text{d}t}$$$
Aplică transformarea Laplace pe ambele părți –
$$U(s)=\left(K_P+\frac{K_I}{s}+K_D s \right )E(s)$$
$$\frac{U(s)}{E(s)}=K_P+\frac{K_I}{s}+K_D s$$$
În concluzie, funcția de transfer a regulatorului proporțional integral derivativ este $K_P + \frac{K_I} {s} + K_D s$.
Diagrama bloc a sistemului de control în buclă închisă cu reacție negativă unitară împreună cu controlerul integral proporțional derivat este prezentată în figura următoare.
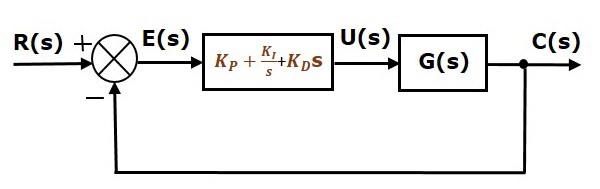
Controlerul integral proporțional derivat este utilizat pentru a îmbunătăți stabilitatea sistemului de control și pentru a diminua eroarea în regim staționar.
.