- Obiective de învățare
- Funcție pe bucățele
- Evaluarea unei funcții definite pe bucăți
- Exemplu
- Exemplu
- Analiză a soluției
- Scrierea unei funcții definite pe bucăți
- Exemplu
- Analiza soluției
- Dată o funcție pe bucățele, scrieți formula și identificați domeniul pentru fiecare interval.
- Graficați funcțiile piecewise
- Dată o funcție pe bucăți, schițați un grafic.
- Exemplu
- Exemplu
- Rezumat
Obiective de învățare
- Introducere la funcțiile pe bucățele
- Definiți funcțiile pe bucățele funcție piecewise
- Evaluați o funcție piecewise
- Scrieți o funcție piecewise având în vedere o aplicație
- Graficați funcții piecewise
- Dată o funcție piecewise-funcție definită în bucăți, schițați un grafic
- Scrieți domeniul și intervalul unei funcții definite pe bucățele, având în vedere un grafic
Câteva funcții vin pe bucățele. În această secțiune, vom învăța cum să definim și să reprezentăm grafic funcții care sunt, în esență, colecții de bucăți discrete. Exemple de ceva definit în acest fel includ proiectarea profilului unei mașini, calcularea planului de telefonie mobilă și calcularea ratelor de impozit pe venit. De exemplu, rata de impozitare depinde de venitul dvs. și este aceeași pentru o gamă de venituri, așa cum se arată în tabelul de mai jos:
| Taxa de impozitare marginală | Reducere impozabilă unică | Căsătorit care depune în comun sau văduv calificat(ă) impozabil(ă) Income | Married Filing Separately Taxable Income | Head of Household Taxable Income |
|---|---|---|---|---|
| 10% | $0 – $9,275 | $0 – $18,550 | $0 – $9,275 | $0 – $13,250 |
| 15% | $9,276 – $37,650 | $18,551 – $75,300 | $9,276 – $37,650 | $13,251 – $50,400 |
| 25% | $37,651 – $91,150 | $75,301 – $151,900 | $37,651 – $75,950 | $50,401 – $130,150 |
| 28% | $91,151 – $190,150 | $151,901 – $231,450 | $75,951 – $115,725 | $130,151 – $210,800 |
| 33% | $190,151 – $413,350 | $231,451 – $413,350 | $115,726 – $206,675 | $210,801 – $413,350 |
| 35% | $413,351 – $415,050 | $413,351 – $466,950 | $206,676 – $233,475 | $413,351 – $441,000 |
| 39.6% | $415,051+ | $466,951+ | $233,476+ | $441,001+ |
O funcție pe bucăți este o funcție în care se utilizează mai mult de o formulă pentru a defini ieșirea pe diferite părți ale domeniului.
Utilizăm funcțiile pe bucăți pentru a descrie situațiile în care o regulă sau o relație se modifică pe măsură ce valoarea de intrare traversează anumite „limite”. De exemplu, întâlnim adesea situații în afaceri pentru care costul pe bucată al unui anumit articol este redus odată ce numărul comandat depășește o anumită valoare. Cotele de impozitare sunt un alt exemplu din lumea reală de funcții pe bucăți. De exemplu, luați în considerare un sistem fiscal simplu în care veniturile de până la 10.000 de dolari sunt impozitate cu 10%, iar orice venit suplimentar este impozitat cu 20%. Impozitul pe un venit total, S, ar fi 0,1S dacă S\le 10.000$ și 1000 + 0,2 (S – 10.000$), dacă S> 10.000$.
Funcție pe bucățele
O funcție pe bucățele este o funcție în care se utilizează mai mult de o formulă pentru a defini rezultatul. Fiecare formulă are propriul său domeniu, iar domeniul funcției este uniunea tuturor acestor domenii mai mici. Notăm această idee în felul următor:
f\left(x\right)=\begin{cases}\text{formula 1 dacă x este în domeniul 1}\\ \text{formula 2 dacă x este în domeniul 2}\ \ text{formula 3 dacă x este în domeniul 3}\end{cases}
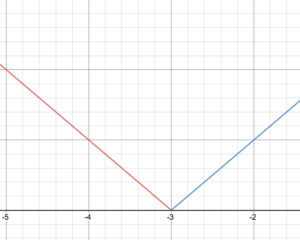
În notația pe bucăți, funcția de valoare absolută este
Evaluarea unei funcții definite pe bucăți
În primul exemplu, vom arăta cum se evaluează o funcție definită pe bucăți. Observați cum este important să acordați atenție domeniului pentru a determina ce expresie să utilizați pentru a evalua intrarea.
Exemplu
Dată funcția
f(x)=\begin{cazuri}7x+3\text{ if }x<0\7x+6\text{ if }x\ge{0}\end{cazuri},
evaluați:
- f (-1)
- f (0)
- f (2)
În videoclipul următor arătăm cum să evaluăm mai multe valori dată o funcție definită fragmentar.
În exemplul următor arătăm cum să evaluăm o funcție care modelează costul transferului de date pentru o companie de telefonie.
Exemplu
O companie de telefonie mobilă folosește funcția de mai jos pentru a determina costul, C, în dolari pentru g gigaocteți de transfer de date.
Găsește costul utilizării 1.5 gigaocteți de date și costul utilizării a 4 gigaocteți de date.
Analiză a soluției
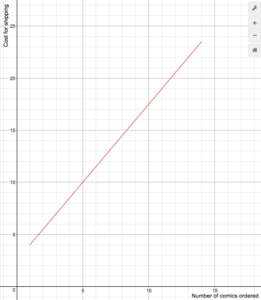
Funcția este reprezentată în graficul de mai jos. Se poate observa unde funcția trece de la o constantă la o dreaptă cu pantă pozitivă la g=2. Trasăm graficele pentru diferitele formule pe un set comun de axe, asigurându-ne că fiecare formulă este aplicată pe domeniul său corespunzător.

C(g) = C\left(g\right)=\begin{cases}{25}\text{ if }{ 0 }<{ g }<{ 2 }\\ 10g+5\text{ if }{ g}\ge{ 2 }\end{cases}
Scrierea unei funcții definite pe bucăți
În ultimul exemplu vom arăta cum să scriem o funcție definită pe bucăți care să modeleze prețul unui tur ghidat la muzeu.
Exemplu
Un muzeu percepe 5 $ de persoană pentru un tur ghidat cu un grup de la 1 la 9 persoane sau o taxă fixă de 50 $ pentru un grup de 10 sau mai multe persoane. Scrieți o funcție care să relaționeze numărul de persoane, n, cu costul, C.
Analiza soluției
Funcția este reprezentată în figura 21. Graficul este o linie diagonală de la n=0 la n=10 și o constantă după aceea. În acest exemplu, cele două formule sunt de acord în punctul de întâlnire unde n=10, dar nu toate funcțiile pe bucățele au această proprietate.

În videoclipul următor prezentăm un exemplu de scriere a unei funcții definite pe bucățele având în vedere un scenariu.
Dată o funcție pe bucățele, scrieți formula și identificați domeniul pentru fiecare interval.
- Identificați intervalele pentru care se aplică reguli diferite.
- Determinați formulele care descriu modul de calcul al unei ieșiri pornind de la o intrare în fiecare interval.
- Utilizați paranteze și declarații if pentru a scrie funcția.
Graficați funcțiile piecewise
În această secțiune, vom reprezenta grafic funcțiile piecewise. Funcția trasată mai jos reprezintă costul de transfer al datelor pentru o anumită companie de telefonie mobilă. Putem vedea unde funcția trece de la o constantă la o dreaptă cu pantă pozitivă la g=2. Atunci când trasăm funcții pe bucăți, este important să ne asigurăm că fiecare formulă este aplicată pe domeniul său corespunzător.C\left(g\right)=\begin{cases}{25} \text{ if }{ 0 }<{ g }<{ 2 }\\10g+5\text{ if }{ g}\ge{ 2 }\end{cases}
În acest caz, rezultatul este 25 pentru orice intrare între 0 și 2. Pentru valori mai mari sau egale cu 2, ieșirea este definită ca fiind 10g+5.

Dată o funcție pe bucăți, schițați un grafic.
- Indicați pe axa x limitele definite de intervalele de pe fiecare bucată a domeniului.
- Pentru fiecare bucată a domeniului, reprezentați grafic pe intervalul respectiv folosind ecuația corespunzătoare care aparține acelei bucăți. Nu reprezentați grafic două funcții pe un singur interval, deoarece ar încălca criteriile unei funcții.
Exemplu
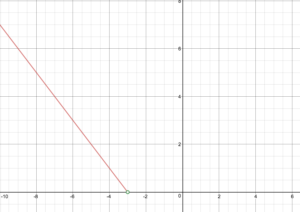
Scrieți un grafic al funcției.
Dată definiția pe bucăți f(x)=\început{cazuri}-x – 3\text{ if }x < -3\\ x + 3\text{ if } x \ge -3\end{cases}
Desenați graficul lui f.
Spuneți domeniul și intervalul funcției.
În următorul exemplu, vom reprezenta grafic o funcție definită fragmentar care modelează costul de expediere pentru un retailer online de benzi desenate.
Exemplu
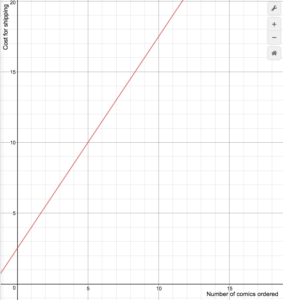
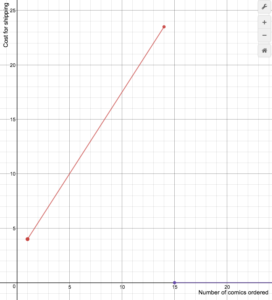
Un retailer online de benzi desenate percepe costurile de expediere conform următoarei formule
S(n)=\begin{cases}1.5n+2.5\text{ if }1\le{n}\le14\\0\text{ if }n\ge15\end{cases}
Desenați un grafic al funcției de cost.
În videoclipul următor arătăm cum să reprezentăm grafic o funcție definită fragmentar care este liniară pe ambele domenii.
Rezumat
- O funcție piecewise este o funcție în care se utilizează mai mult de o formulă pentru a defini ieșirea pe diferite părți ale domeniului.
- Evaluarea unei funcții piecewise înseamnă că trebuie să acordați o atenție deosebită expresiei corecte utilizate pentru intrarea dată
Pentru a reprezenta grafic funcțiile piecewise, mai întâi identificați unde este împărțit domeniul. Reprezentați grafic funcțiile pe domeniu folosind instrumente precum punctele de trasare sau transformările. Aveți grijă să folosiți cercuri deschise sau închise pe punctele finale ale fiecărui domeniu, în funcție de faptul dacă punctul final este sau nu inclus.
.