Circuitul Adder jumătate și Adder complet
Circuitele Adder jumătate și Adder complet sunt explicate cu tabelele lor de adevăr în acest articol. Este prezentată, de asemenea, proiectarea unui sumator complet folosind circuitul Half Adder. Se prezintă, de asemenea, circuitul Full Adder pe un singur bit și adunarea pe mai mulți biți folosind Full Adder.
Înainte de a intra în acest subiect, este foarte important să știți despre logica booleană și porțile logice.
EXAMINĂ: LOGICĂ BOOLEANĂ
EXAMINĂ: PORȚI LOGICE
EXAMINĂ: FLIP FLOPS
Ce este un sumator?
Un sumator este un tip de calculator care este folosit pentru a adăuga două numere binare. Când spun, calculator, nu mă refer la unul cu butoane, acesta este un circuit care poate fi integrat cu multe alte circuite pentru o gamă largă de aplicații. Există două tipuri de sumatoare;
- Jumătate de sumator
- Sumator complet
Jumătate de sumator
Cu ajutorul jumătății de sumator, putem proiecta circuite capabile să efectueze adunări simple cu ajutorul porților logice.
Să ne uităm mai întâi la adunarea de biți simpli.
0+0 = 0
0+1 = 1
1+0 = 1
1+1 = 10
Acestea sunt cele mai puține combinații posibile de biți simpli. Dar rezultatul pentru 1+1 este 10. Deși această problemă poate fi rezolvată cu ajutorul unei porți EXOR, dacă vă interesează ieșirea, rezultatul sumei trebuie rescris ca o ieșire pe 2 biți.
Așa, ecuațiile de mai sus pot fi scrise ca
0+0 = 00
0+1 = 01
1+0 = 01
1+1 = 10
Aici, ieșirea „1” din „10” devine rezultatul de reportare. Rezultatul este prezentat în tabelul de adevăr de mai jos. ‘SUM’ este ieșirea normală, iar ‘CARRY’ este rezultatul transferului.
INTRĂRI Ieșiri
A B SUM CARRY
0 0 0 0
0 1 1 0
1 0 1 0 0
1 1 0 1
Din ecuația, este clar că acest sumator pe 1 bit poate fi implementat cu ușurință cu ajutorul unei porți EXOR pentru ieșirea „SUM” și a unei porți AND pentru transport. Aruncați o privire la implementarea de mai jos.
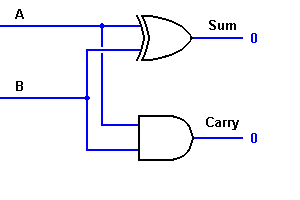
Pentru adunări complexe, pot exista cazuri în care trebuie să adunați doi octeți de 8 biți. Acest lucru se poate face numai cu ajutorul logicii full-adder.
Full Adder
Acest tip de sumator este un pic mai dificil de implementat decât un half-adder. Principala diferență între o jumătate de adunare și o adunare completă este că adunarea completă are trei intrări și două ieșiri. Primele două intrări sunt A și B, iar cea de-a treia intrare este o intrare de transport desemnată ca CIN. Atunci când este proiectată o logică de adunare completă, vom putea să înșirăm opt dintre ele împreună pentru a crea o adunare la nivel de byte și să punem în cascadă bitul de transport de la un adunator la altul.
Contractul de transport de la ieșire este desemnat ca COUT, iar ieșirea normală este desemnată ca S. Aruncați o privire la tabelul de adevăr.
INTRĂRI IEȘIRI
A B CIN COUT S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 0 1
0 1 1 1 1 0
1 0 0 0 0 1
1 0 1 1 0
1 1 0 1 0 0
1 1 1 1 1 1 1
Din adevărul de mai sus-tabel de adevăr, poate fi implementată logica sumatorului complet. Putem observa că ieșirea S este un EXOR între intrarea A și ieșirea SUM a semiagregătorului cu intrările B și CIN. Trebuie să observăm, de asemenea, că COUT va fi adevărat numai dacă oricare dintre cele două intrări din cele trei sunt HIGH.
Așa, putem implementa un circuit sumator complet cu ajutorul a două circuite semisumatoare. Primul semiagregator va fi utilizat pentru a adăuga A și B pentru a produce o sumă parțială. A doua jumătate de sumator logic poate fi utilizată pentru a adăuga CIN la suma produsă de prima jumătate de sumator pentru a obține ieșirea finală S. Dacă oricare dintre cele două jumătăți logice ale sumatorului produce un transport, va exista un transport la ieșire. Astfel, COUT va fi o funcție OR a ieșirilor de transport ale semiagregătorului. Aruncați o privire la implementarea circuitului de adunare completă prezentată mai jos.
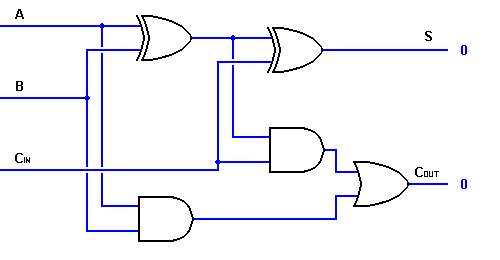
Chiar dacă implementarea unor diagrame logice mai mari este posibilă cu logica de adunare completă de mai sus, un simbol mai simplu este utilizat de cele mai multe ori pentru a reprezenta operația. Mai jos este prezentată o reprezentare schematică mai simplă a unui sumator complet pe un bit.
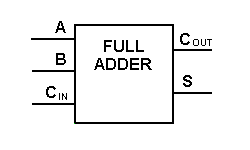
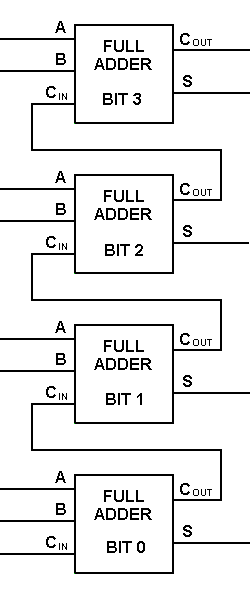
Cu acest tip de simbol, putem aduna doi biți luând un transport de la următorul ordin de mărime inferior și trimițând un transport la următorul ordin de mărime superior. Într-un calculator, pentru o operație pe mai mulți biți, fiecare bit trebuie să fie reprezentat de un sumator complet și trebuie să fie adăugat simultan. Astfel, pentru a aduna două numere pe 8 biți, veți avea nevoie de 8 aditivi complecși care pot fi formați prin cascada a două dintre blocurile de 4 biți. Adăugarea a două numere pe 4 biți este prezentată mai jos.