Formula standard pentru aflarea determinantului unei matrice 3×3 este o descompunere a unor probleme mai mici de determinant 2×2, care sunt foarte ușor de rezolvat. Dacă aveți nevoie de o reîmprospătare, consultați cealaltă lecție a mea despre cum se găsește determinantul unei matrice 2×2. Să presupunem că ni se dă o matrice pătrată A în care,
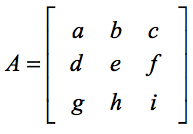
Determinantul matricei A se calculează ca
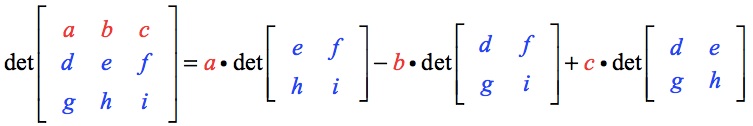
Iată care sunt punctele cheie:
- Observați că elementele din rândul de sus, și anume a, b și c servesc ca multiplicatori scalari pentru o matrice 2×2 corespunzătoare.
- Scalarul a este multiplicat la matricea 2×2 a elementelor rămase create atunci când se trasează segmente de linie verticală și orizontală care trec prin a.
- Același proces este aplicat pentru a construi matricele 2×2 pentru multiplicatorii scalari b și c.
Determinantul unei matrici 3 x 3 (animat)

Exemple de găsire a determinantului unei matrici 3×3
Exemplu 1: Găsiți determinantul matricei 3×3 de mai jos.
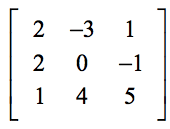
Stabilirea de mai jos vă va ajuta să găsiți corespondența dintre elementele generice ale formulei și elementele problemei reale.
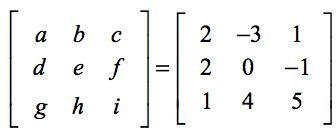
Aplicând formula,


Exemplul 2: Evaluați determinantul matricei 3×3 de mai jos.
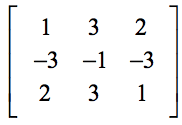
Să fiți foarte atenți când înlocuiți valorile în locurile potrivite din formulă. Erori frecvente apar atunci când elevii devin neglijenți în timpul etapei inițiale de substituire a valorilor.
În plus, nu vă grăbiți să vă asigurați că și aritmetica este corectă. În caz contrar, o singură eroare undeva în calcul va produce un răspuns greșit în final.
Din moment ce,
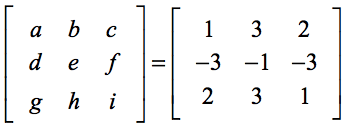
calculul nostru al determinantului devine…

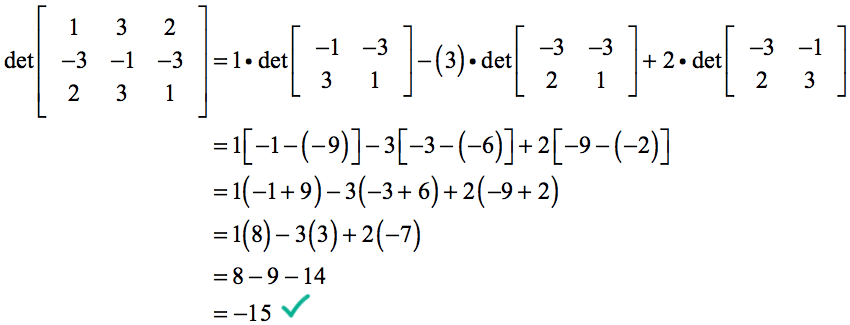
Exemplul 3: Rezolvați determinantul matricei 3×3 de mai jos.
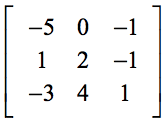
Prezența lui zero (0) în primul rând ar trebui să ne ușureze mult calculul. Amintiți-vă, acele elemente din primul rând, acționează ca multiplicatori scalari. Prin urmare, zero înmulțit cu orice, va duce la dispariția întregii expresii.
.