- OBIECTIVE DE ÎNVĂȚARE
- Exemplu 1. Calculul energiei eliberate prin fisiune
- Strategie
- Soluție
- Discuție
- Exemplu 2. Calcularea energiei dintr-un kilogram de combustibil fisionabil
- Strategie
- Soluție
- Discuție
- Explorări PhET: fisiunea nucleară
- Rezumat al secțiunii
- Întrebări conceptuale
- Probleme &Exerciții
- Glosar
- Soluții alese la probleme &Exerciții
OBIECTIVE DE ÎNVĂȚARE
La sfârșitul acestei secțiuni, veți fi capabili să:
- Definiți fisiunea nucleară.
- Să discutați cum reacționează combustibilul de fisiune și să descrieți ce produce.
- Să descrieți reacțiile în lanț controlate și necontrolate.
Fisiunea nucleară este o reacție în care un nucleu este divizat (sau fisurat). Fisiunea controlată este o realitate, în timp ce fuziunea controlată este o speranță pentru viitor. Sute de centrale nucleare de fisiune din întreaga lume atestă faptul că fisiunea controlată este practică și, cel puțin pe termen scurt, economică, după cum se vede în figura 1. În timp ce energia nucleară a prezentat un interes scăzut timp de zeci de ani, după TMI și Cernobîl (și acum Fukushima Daiichi), preocupările crescânde legate de încălzirea globală au readus energia nucleară pe tapet ca alternativă energetică viabilă. La sfârșitul anului 2009, existau 442 de reactoare în funcțiune în 30 de țări, furnizând 15% din energia electrică mondială. Franța furnizează peste 75% din energia electrică pe bază de energie nucleară, în timp ce SUA au 104 reactoare în funcțiune care furnizează 20% din energia electrică. Australia și Noua Zeelandă nu au niciunul. China construiește centrale nucleare în ritmul de un început în fiecare lună.

Figura 1. Oamenii care locuiesc în apropierea acestei centrale nucleare nu au nicio expunere măsurabilă la radiații care să poată fi atribuite centralei. Aproximativ 16% din energia electrică din lume este generată prin fisiune nucleară controlată în astfel de centrale. Turnurile de răcire sunt cele mai proeminente caracteristici, dar nu sunt unice pentru energia nucleară. Reactorul se află în mica clădire în formă de cupolă din stânga turnurilor. (credit: Kalmthouts)
Fisiunea este opusul fuziunii și eliberează energie doar atunci când nucleele grele sunt divizate. După cum s-a menționat în Fuziune, energia este eliberată dacă produsele unei reacții nucleare au o energie de legătură pe nucleon (BE/A) mai mare decât nucleele mamă. Figura 2 arată că BE/A este mai mare pentru nucleele de masă medie decât pentru nucleele grele, ceea ce implică faptul că, atunci când un nucleu greu este divizat, produsele au mai puțină masă pe nucleon, astfel încât masa este distrusă și energia este eliberată în reacție. Cantitatea de energie per reacție de fisiune poate fi mare, chiar și după standardele nucleare. Graficul din figura 2 arată că BE/A este de aproximativ 7,6 MeV/nucleon pentru cele mai grele nuclee (A aproximativ 240), în timp ce BE/A este de aproximativ 8,6 MeV/nucleon pentru nuclee cu A aproximativ 120. Astfel, dacă un nucleu greu se împarte în două, atunci se eliberează aproximativ 1 MeV per nucleon, sau aproximativ 240 MeV per fisiune. Aceasta este de aproximativ 10 ori mai mare decât energia pe reacție de fuziune și de aproximativ 100 de ori mai mare decât energia medie a dezintegrării α, β sau γ.
Exemplu 1. Calculul energiei eliberate prin fisiune
Calculați energia eliberată în următoarea reacție de fisiune spontană:
238U → 95Sr + 140Xe + 3n
După masele atomice fiind m(238U) = 238.050784 u, m(95Sr) = 94,919388 u, m(140Xe) = 139,921610 u, iar m(n) =1,008665 u.
Strategie
Ca întotdeauna, energia eliberată este egală cu masa distrusă înmulțită cu c2, deci trebuie să găsim diferența de masă dintre 238U părinte și produșii de fisiune.
Soluție
Produsele au o masă totală de
\begin{array}{lll}{m}_{\text{produși}}& =& 94.919388\text{ u}+139.921610 \text{ u}+3\left(1.008665\text{ u}\right)\\ & =& 237.866993\text{ u}\end{array}\\\
Masa pierdută este masa de 238U minus mprodus, sau
deci energia eliberată este
\begin{array}{lll}E& =& \left(\Delta m\right){c}^{2}\\ & =& \left(0.183791\text{ u}\right)\frac{931.5\text{ Me}\text{V/}{c}^{2}}}{\text{u}}{c}^{2}=171.2\text{ MeV}\end{array}\\
Discuție
În acest exemplu apar o serie de lucruri importante. Energia de 171 MeV eliberată este mare, dar puțin mai mică decât cea estimată anterior, de 240 MeV. Acest lucru se datorează faptului că această reacție de fisiune produce neutroni și nu scindează nucleul în două părți egale. Fisiunea unui anumit nuclid, cum ar fi 238U , nu produce întotdeauna aceiași produși. Fisiunea este un proces statistic în care se produce o întreagă gamă de produse cu diferite probabilități. Cea mai mare parte a fisiunii produce neutroni, deși numărul acestora variază la fiecare fisiune. Acesta este un aspect extrem de important al fisiunii, deoarece neutronii pot induce mai multe fisiuni, permițând reacții în lanț care se întrețin singure.
Se poate produce fisiunea spontană, dar, de obicei, acesta nu este cel mai frecvent mod de dezintegrare pentru un anumit nuclid. De exemplu, 238U poate fisiona spontan, dar se dezintegrează în principal prin emisie α. Fisiunea indusă de neutroni este crucială, după cum se vede în figura 2. Fiind lipsiți de sarcină, chiar și neutronii de energie scăzută pot lovi un nucleu și pot fi absorbiți odată ce simt forța nucleară atractivă. Nucleii mari sunt descriși printr-un model de picătură lichidă cu tensiune superficială și moduri de oscilație, deoarece numărul mare de nucleoni acționează ca atomii într-o picătură. Neutronul este atras și, astfel, depune energie, determinând nucleul să se deformeze ca o picătură de lichid. Dacă este întins suficient, nucleul se îngustează în mijloc. Numărul de nucleoni în contact și intensitatea forței nucleare care leagă nucleul între ele se reduc. Repulsia coulombiană între cele două capete reușește apoi să fisureze nucleul, care se sparge ca o picătură de apă în două bucăți mari și câțiva neutroni. Fisiunea indusă de neutroni poate fi scrisă sub forma
n + AX → FF1 + FF2 + xn,
unde FF1 și FF2 sunt cele două nuclee fiice, numite fragmente de fisiune, iar x este numărul de neutroni produși. De cele mai multe ori, masele fragmentelor de fisiune nu sunt identice. Cea mai mare parte a energiei eliberate se transformă în energie cinetică a fragmentelor de fisiune, iar restul se transformă în neutroni și în stările excitate ale fragmentelor. Deoarece neutronii pot induce fisiunea, este posibilă o reacție în lanț autoîntreținută, cu condiția ca mai mult de un neutron să fie produs în medie – adică, dacă x>1 în n + AX → FF1 + FF2 + xn. Acest lucru poate fi observat și în figura 3. Un exemplu de reacție tipică de fisiune indusă de neutroni este
n+{}_{\text{92}}^{\text{235}}\text{U}\la {}_{\text{56}}^{\text{142}}\text{Ba}+{}_{\text{36}}}^{\text{91}}\text{Kr}+3\text{n}\\\.
Rețineți că în această ecuație, sarcina totală rămâne aceeași (se conservă): 92 + 0 = 56 + 36. De asemenea, în ceea ce privește numerele întregi, masa este constantă: 1 + 235 = 142 + 91 + 3. Acest lucru nu este adevărat atunci când considerăm masele până la 6 sau 7 cifre semnificative, ca în exemplul anterior.

Figura 2. Este prezentată fisiunea indusă de neutroni. În primul rând, energia este pusă în acest nucleu mare atunci când acesta absoarbe un neutron. Acționând ca o picătură de lichid lovită, nucleul se deformează și începe să se îngusteze în mijloc. Deoarece mai puțini nucleoni sunt în contact, forța repulsivă a lui Coulomb este capabilă să rupă nucleul în două părți, unii neutroni zburând de asemenea.

Figura 3. O reacție în lanț poate produce fisiune autoîntreținută dacă fiecare fisiune produce suficienți neutroni pentru a induce cel puțin încă o fisiune. Acest lucru depinde de mai mulți factori, inclusiv de numărul de neutroni produși într-o fisiune medie și de ușurința cu care se poate produce fisiunea unui anumit tip de nuclid.
Nu fiecare neutron produs prin fisiune induce fisiunea. Unii neutroni scapă din materialul fisionabil, în timp ce alții interacționează cu un nucleu fără a-l face să fisioneze. Putem spori numărul de fisiuni produse de neutroni dacă avem o cantitate mare de material fisionabil. Cantitatea minimă necesară pentru fisiunea autosusținută a unui anumit nucleid se numește masa critică a acestuia. Unii nuclizi, cum ar fi 239Pu, produc mai mulți neutroni pe fisiune decât alții, cum ar fi 235U . În plus, unii nuclizi sunt mai ușor de fisionat decât alții. În special, 235U și 239Pu, sunt mai ușor de fisionat decât mult mai abundentul 238U . Ambii factori afectează masa critică, care este cea mai mică pentru 239Pu.
Motivul pentru care 235U și 239Pu sunt mai ușor de fisionat decât 238U este că forța nucleară este mai atractivă pentru un număr par de neutroni într-un nucleu decât pentru un număr impar. Să considerăm că {}_{{\text{92}}^{\text{235}}{\text{U}}_{text{143}}\\ are 143 de neutroni, iar {}_{\text{94}}^{\text{239}}{\text{P}}_{\text{145}}\ are 145 de neutroni, în timp ce {}_{\text{92}}}^{\text{238}}{\text{U}}_{text{146}}\ are 146 de neutroni. Atunci când un neutron întâlnește un nucleu cu un număr impar de neutroni, forța nucleară este mai atractivă, deoarece neutronul suplimentar va face ca numărul neutronilor să fie egal. În nucleul rezultat se depune cu aproximativ 2 MeV mai multă energie decât în cazul în care numărul neutronilor ar fi fost deja par. Această energie suplimentară produce o deformare mai mare, ceea ce face ca fisiunea să fie mai probabilă. Astfel, 235U și 239Pu sunt combustibili de fisiune superiori. Izotopul 235U reprezintă doar 0,72% din uraniul natural, în timp ce 238U reprezintă 99,27%, iar 239Pu nu există în natură. Australia are cele mai mari depozite de uraniu din lume, reprezentând 28% din total. Aceasta este urmată de Kazahstan și Canada. SUA deține doar 3% din rezervele globale.
Majoritatea reactoarelor de fisiune utilizează 235U , care este separat de 238U cu anumite cheltuieli. Acest lucru se numește îmbogățire. Cea mai comună metodă de separare este difuzia gazoasă a hexafluorurii de uraniu (UF6) prin membrane. Deoarece 235U are o masă mai mică decât 238U , moleculele sale de UF6 au o viteză medie mai mare la aceeași temperatură și difuzează mai repede. O altă caracteristică interesantă a 235U este aceea că absoarbe în mod preferențial neutronii cu mișcare foarte lentă (cu energii de o fracțiune de eV), în timp ce reacțiile de fisiune produc neutroni rapizi cu energii de ordinul unui MeV. Pentru a realiza un reactor de fisiune autoîntreținută cu 235U , este, prin urmare, necesară încetinirea („termalizarea”) neutronilor. Apa este foarte eficientă, deoarece neutronii se ciocnesc cu protonii din moleculele de apă și pierd energie. Figura 4 prezintă o schemă a unui proiect de reactor, numit reactor cu apă presurizată.

Figura 4. Un reactor cu apă presurizată este proiectat inteligent pentru a controla fisiunea unor cantități mari de 235U , utilizând în același timp căldura produsă în reacția de fisiune pentru a crea abur pentru a genera energie electrică. Barele de control reglează fluxul de neutroni astfel încât să se obțină criticitatea, dar să nu fie depășită. În cazul în care reactorul se supraîncălzește și fierbe apa, reacția în lanț se termină, deoarece apa este necesară pentru a termaliza neutronii. Această caracteristică de siguranță inerentă poate fi depășită în circumstanțe extreme.
Pentru reglarea fluxului de neutroni se folosesc bare de control care conțin nuclizi care absorb foarte puternic neutronii. Pentru a produce o putere mare, reactoarele conțin sute până la mii de mase critice, iar reacția în lanț devine cu ușurință autoîntreținută, o condiție numită criticitate. Fluxul de neutroni trebuie să fie reglat cu atenție pentru a evita o creștere exponențială a fisiunilor, o condiție numită supercriticitate. Barele de control ajută la prevenirea supraîncălzirii, poate chiar a unei fuziuni sau a unei dezmembrări explozive. Apa care este utilizată pentru a termaliza neutronii, necesară pentru ca aceștia să inducă fisiunea în 235U și să atingă criticitatea, oferă un feedback negativ pentru creșterea temperaturii. În cazul în care reactorul se supraîncălzește și fierbe apa până la abur sau este fisurat, absența apei ucide reacția în lanț. Cu toate acestea, o căldură considerabilă poate fi în continuare generată de produsele radioactive de fisiune ale reactorului. Prin urmare, în cazul unui accident de pierdere a agentului de răcire trebuie încorporate și alte elemente de siguranță, inclusiv apă și pompe de răcire auxiliare.
Exemplu 2. Calcularea energiei dintr-un kilogram de combustibil fisionabil
Calculați cantitatea de energie produsă prin fisiunea a 1,00 kg de 235U , având în vedere că reacția medie de fisiune a 235U produce 200 MeV.
Strategie
Energia totală produsă este reprezentată de numărul de atomi de 235U înmulțit cu energia dată per fisiune de 235 U. Prin urmare, trebuie să aflăm numărul de atomi de 235U din 1,00 kg.
Soluție
Numărul de atomi de 235U din 1,00 kg este numărul lui Avogadro înmulțit cu numărul de moli. Un mol de 235U are o masă de 235,04 g; astfel, există (1000 g)/(235,04 g/mol) = 4,25 moli. Prin urmare, numărul de atomi de 235U este,
\left(4,25 \text{ mol}\right)\left(6,02\ ori {10}^{23}{}^{{{235}\text{U/mol}\right)=2.56\times{10}^{24}{}^{text{ 235}\text{U}\\\\}.
Atunci energia totală eliberată este
\begin{array}{lll}E & =& \left(2.56\ ori {10}^{24}{}^{235}\text{U}\right)\left(\frac{200\text{ MeV}}{{{}^{\text{235}}\text{U}}\right)\left(\frac{1.60\ ori {10}^{-13}\text{ J}}{\text{MeV}}\right)\\ & =& 8.21\times {10}^{{13}\text{ J}\end{array}\\\r\.
Discuție
Aceasta este o altă cantitate impresionant de mare de energie, echivalentă cu aproximativ 14.000 de barili de țiței sau 600.000 de galoane de benzină. Dar, este doar o pătrime din energia produsă de fuziunea unui amestec de un kilogram de deuteriu și tritiu, așa cum s-a văzut în exemplul 1. Calcularea energiei și a puterii din fuziune. Chiar dacă fiecare reacție de fisiune produce o energie de aproximativ zece ori mai mare decât o reacție de fuziune, energia pe kilogram de combustibil de fisiune este mai mică, deoarece există mult mai puțini moli pe kilogram de nuclizi grei. Combustibilul de fisiune este, de asemenea, mult mai rar decât cel de fuziune și mai puțin de 1% din uraniu (235U) este ușor de utilizat.
Unul dintre nuclizii deja menționați este 239Pu, care are un timp de înjumătățire de 24.120 de ani și nu există în natură. Plutoniul-239 este fabricat din 238U în reactoare și oferă o oportunitate de a utiliza celelalte 99% din uraniul natural ca sursă de energie. Următoarea secvență de reacție, numită reproducere, produce 239Pu. Reproducerea începe cu captarea neutronilor de către 238U :
Uraniul-239 se dezintegrează apoi prin β-:
239U → 239Np + β- + ve(t1/2 = 23 min).
Neptuniu-239 de asemenea se dezintegrează β-:
239Np → 239Pu + β- + ve(t1/2 = 2,4 d).
Plutoniul-239 se acumulează în combustibilul reactorului la o rată care depinde de probabilitatea de captare a neutronilor de către 238U (tot combustibilul reactorului conține mai mult 238U decât 235U). Reactoarele concepute special pentru a produce plutoniu se numesc reactoare de reproducere. Acestea par a fi în mod inerent mai periculoase decât reactoarele convenționale, dar nu se știe încă dacă pericolele lor pot fi făcute acceptabile din punct de vedere economic. Cele patru reactoare de la Cernobîl, inclusiv cel care a fost distrus, au fost construite pentru a genera plutoniu și a produce energie electrică. Aceste reactoare aveau un design semnificativ diferit de cel al reactorului cu apă presurizată ilustrat mai sus. Plutoniul 239 are avantaje față de 235U ca și combustibil de reactor – produce în medie mai mulți neutroni pe fisiune și este mai ușor pentru un neutron termic să provoace fisiunea acestuia. De asemenea, este diferit din punct de vedere chimic de uraniu, astfel încât este mai ușor de separat din minereul de uraniu. Acest lucru înseamnă că 239Pu are o masă critică deosebit de mică, un avantaj pentru armele nucleare.
Explorări PhET: fisiunea nucleară
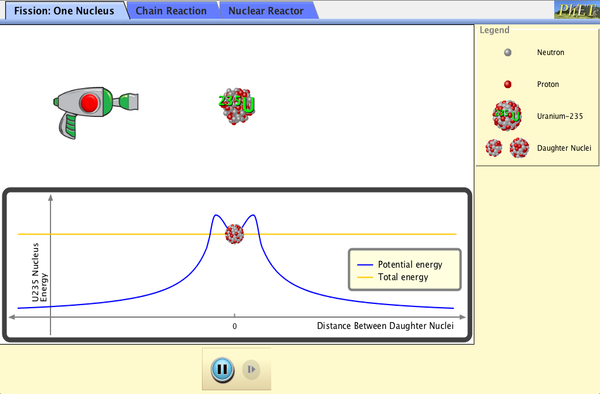
Click pentru a descărca simularea. Rulați folosind Java.
Rezumat al secțiunii
- Fisiunea nucleară este o reacție în care un nucleu este divizat.
- Fisiunea eliberează energie atunci când nucleele grele sunt divizate în nuclee de masă medie.
- Fisiunea autoîntreținută este posibilă, deoarece fisiunea indusă de neutroni produce, de asemenea, neutroni care pot induce alte fisiuni, n + AX → FF1 + FF2 + xn, unde FF1 și FF2 sunt cele două nuclee fiice, sau fragmente de fisiune, iar x este numărul de neutroni produși.
- O masă minimă, numită masă critică, trebuie să fie prezentă pentru a se obține criticitatea.
- Mai mult decât masa critică poate produce supercriticitate.
- Producerea de izotopi noi sau diferiți (în special 239Pu) prin transformare nucleară se numește reproducere, iar reactoarele proiectate în acest scop se numesc reactoare de reproducere.
Întrebări conceptuale
- Explicați de ce fisiunea nucleelor grele eliberează energie. În mod similar, de ce este necesar un aport de energie pentru fisiunea nucleelor ușoare?
- Explicați, în termeni de conservare a momentului și a energiei, de ce ciocnirile neutronilor cu protoni vor termaliza neutronii mai bine decât ciocnirile cu oxigenul.
- Reziduurile reactorului de la Cernobîl sunt înglobate într-o structură uriașă de beton construită în jurul acestuia după accident. O parte din ploaie pătrunde în clădire în timpul iernii, iar radioactivitatea din clădire crește. Ce presupune acest lucru că se întâmplă în interior?
- Din moment ce nucleul de uraniu sau de plutoniu se fisurează în mai multe fragmente de fisiune a căror distribuție masică acoperă o gamă largă de piese, v-ați aștepta la mai multă radioactivitate reziduală din fisiune decât din fuziune? Explicați.
- Nucleul unui reactor nuclear generează o cantitate mare de energie termică din dezintegrarea produșilor de fisiune, chiar și atunci când reacția în lanț de fisiune producătoare de energie este oprită. Această căldură reziduală ar fi mai mare după ce reactorul a funcționat pentru o perioadă lungă sau scurtă de timp? Ce se întâmplă dacă reactorul a fost oprit timp de luni de zile?
- Cum poate un reactor nuclear să conțină multe mase critice și să nu devină supercritic? Ce metode sunt folosite pentru a controla fisiunea în reactor?
- De ce nucleele grele cu număr impar de neutroni pot fi induse la fisiune cu neutroni termici, în timp ce cele cu număr par de neutroni necesită un aport mai mare de energie pentru a induce fisiunea?
- De ce un reactor nuclear convențional cu fisiune nu poate exploda ca o bombă?
Probleme &Exerciții
1. (a) Calculați energia eliberată în fisiunea indusă de neutroni (asemănătoare cu fisiunea spontană din exemplul 1. Calculul energiei eliberate prin fisiune)
datorită m(96Sr) = 95,921750 u și m(140Xe) = 139,92164. (b) Acest rezultat este cu aproximativ 6 MeV mai mare decât rezultatul pentru fisiunea spontană. De ce? (c) Confirmați că numărul total de nucleoni și sarcina totală se conservă în această reacție.
2. (a) Calculați energia eliberată în reacția de fisiune indusă de neutroni
datorită m(92Kr) = 91. (b) Calculați energia eliberată în reacția de fisiune indusă de neutroni
(b) Confirmați că numărul total de nucleoni și sarcina totală sunt conservate în această reacție.
3. (a) Calculați energia eliberată în reacția de fisiune indusă de neutroni
datorită m(96Sr) = 95,921750 u și m(140Ba) = 139,910581 u.
(b) Confirmați că numărul total de nucleoni și sarcina totală se conservă în această reacție.
4. Confirmați că fiecare dintre reacțiile enumerate pentru reproducerea plutoniului imediat după exemplul 2. Calcularea energiei dintr-un kilogram de combustibil fisionabil se conservă numărul total de nucleoni, sarcina totală și numărul familiei de electroni.
5. Reproducerea plutoniului produce energie chiar înainte ca orice plutoniu să fie fisionat. (Scopul principal al celor patru reactoare nucleare de la Cernobîl era reproducerea plutoniului pentru arme. Energia electrică a fost un produs secundar utilizat de populația civilă). Calculați energia produsă în fiecare dintre reacțiile enumerate pentru obținerea plutoniului, imediat după exemplul 2. Calcularea energiei produse de un kilogram de combustibil fisionabil. Masele relevante sunt m(239U) = 239,054289 u, m(239Np) = 239,052932 u și m(239Pu) = 239,052157 u.
6. Izotopul radioactiv natural 232Th nu este un bun combustibil de fisiune, deoarece are un număr par de neutroni; cu toate acestea, el poate fi transformat într-un combustibil adecvat (la fel cum 238U este transformat în 239P).
(a) Care sunt Z și N pentru 232Th?
(b) Scrieți ecuația reacției pentru neutronul captat de 232Th și identificați nuclidul AX produs în n + 232Th → AX + γ.
(c) Nucleul produs β- se dezintegrează, la fel ca și fiica sa. Scrieți ecuațiile de dezintegrare pentru fiecare dintre ele și identificați nucleul final.
(d) Confirmați că nucleul final are un număr impar de neutroni, ceea ce îl face un combustibil de fisiune mai bun.
(e) Căutați timpul de înjumătățire al nucleului final pentru a vedea dacă acesta trăiește suficient de mult pentru a fi un combustibil util.
7. Puterea electrică de ieșire a unei mari instalații de reactor nuclear este de 900 MW. Aceasta are un randament de 35,0% în conversia energiei nucleare în energie electrică.
(a) Care este producția de energie nucleară termică în megawați?
(b) Câte nuclee 235U fizionează în fiecare secundă, presupunând că fisiunea medie produce 200 MeV?
(c) Ce masă de 235U este fisiată într-un an de funcționare la putere maximă?
8. Un mare reactor de putere care a funcționat timp de câteva luni este oprit, dar activitatea reziduală din miez produce încă 150 MW de energie. Dacă energia medie pe dezintegrare a produselor de fisiune este de 1,00 MeV, care este activitatea nucleului în curies?
Glosar
reactoare de reproducere: reactoare care sunt proiectate special pentru a produce plutoniu reproducere: proces de reacție care produce 239Pu criticitate: condiție în care o reacție în lanț devine cu ușurință autoîntreținută masă critică: cantitatea minimă necesară pentru fisiunea autoîntreținută a unui anumit nuclid fragmente de fisiune: un nucleu fiică modelul picăturii lichide: un model de nucleu (doar pentru a înțelege unele caracteristici ale acestuia) în care nucleonii dintr-un nucleu se comportă ca atomii dintr-o picătură fisiune nucleară fisiune nucleară: reacție în care un nucleu se scindează fisiune indusă de neutroni: fisiune care este inițiată după absorbția unui neutron supercriticitate: o creștere exponențială a fisiunilor
Soluții alese la probleme &Exerciții
1. (a) 177,1 MeV (b) Deoarece câștigul unui neutron extern produce aproximativ 6 MeV, ceea ce reprezintă media BE/A pentru nucleele grele. (c) A = 1 + 238 = 96 + 140 + 1 + 1 + 1 + 1, Z = 92 = 38 + 53, efn = 0 = 0
3. (a) 180,6 MeV (b) A = 1 + 239 = 96 + 140 + 1 + 1 + 1 + 1 + 1, Z = 94 = 38 + 56, efn = 0 = 0
5. 238U + n → 239U + γ 4. (b) A = 1 + 239 = 96 + 140 + 1 + 1 + 1 + 1 + 1, Z = 94 = 38 + 56, efn = 0 = 0
6.81 MeV
239U → 239Np + β- + ve 0,753 MeV
239Np → 239Pu + β- + ve 0,211 MeV
7. (a) 2,57 × 103 MW (b) 8,03 × 1019 fisiuni/s (c) 991 kg
.