Să începem prin a examina împărțirea valorilor cu exponenți.
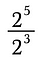
Reamintim că exponenții reprezintă înmulțiri repetate. Deci putem rescrie expresia de mai sus sub forma:
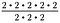
Din moment ce 2/2 = 1, se anulează trei seturi de 2/2. Rămâne 2 – 2, sau 2 la pătrat.
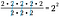
Desigur că putem lua o scurtătură și să scădem numărul de 2 de jos din numărul de 2 de sus. Deoarece aceste cantități sunt reprezentate de exponenții respectivi, tot ce trebuie să facem este să scriem baza comună cu diferența valorilor exponenților ca putere.
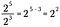
Dacă generalizăm această regulă, avem următoarea, unde n reprezintă un număr real diferit de zero, iar x și y sunt tot numere reale.
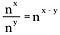
Explorarea puterii zero
De aici este ușor de dedus explicația pentru care orice număr diferit de zero ridicat la puterea zero este egal cu 1. Din nou, să ne uităm la un exemplu concret.
Știm că orice număr diferit de zero împărțit la el însuși este egal cu 1. Așadar, pot scrie următoarele:
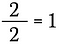
Acest lucru este același lucru cu a scrie:
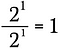
Acum voi utiliza regula exponentului de mai sus pentru a rescrie partea stângă a acestei ecuații.
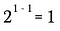
Desigur, aceasta este echivalentă cu:
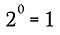
Potem folosi același procedeu ca în acest exemplu, împreună cu regula generalizată de mai sus, pentru a arăta că orice număr real diferit de zero ridicat la puterea zero trebuie să rezulte 1.
Cum rămâne cu zero la puterea zero?
Aici lucrurile devin dificile. Metoda de mai sus se strică pentru că, desigur, împărțirea la zero este interzisă. Să examinăm de ce.
Vom începe prin a examina un ERROR comun de împărțire la zero.
Ce ziceți de 2÷0? Să analizăm de ce nu putem face acest lucru.
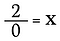
Diviziunea este de fapt doar o formă de înmulțire, deci ce se întâmplă dacă rescriu ecuația de mai sus sub forma: :
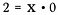
Ce valoare ar putea satisface această ecuație pentru x?
Nu există nicio valoare! Orice număr înmulțit cu zero are ca rezultat zero, nu poate fi niciodată egal cu 2. Prin urmare, spunem că împărțirea la zero este nedefinită. Nu există nicio soluție posibilă.
Acum să ne uităm la 0÷0.
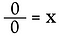
Încă o dată, rescrieți-o ca pe o problemă de înmulțire.
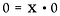
Aici întâlnim o situație foarte diferită. Soluția pentru x ar putea fi ORICE număr real! Nu există nicio modalitate de a determina care este x. Prin urmare, 0/0 este considerat nedeterminat*, nu nedefinit.
Dacă încercăm să folosim metoda de mai sus cu zero ca bază pentru a determina ce ar fi zero la puterea zero, ne oprim imediat și nu putem continua pentru că știm că 0÷0 ≠ 1, dar este nedeterminat.
Atunci ce este egal cu zero la puterea zero?
Acest lucru este foarte dezbătut. Unii cred că ar trebui definit ca fiind 1, în timp ce alții cred că este 0, iar unii cred că este nedefinit. Există argumente matematice bune pentru fiecare, și poate că cel mai corect este să fie considerat nedeterminat.
În ciuda acestui fapt, comunitatea matematică este în favoarea definirii lui zero la puterea zero ca fiind 1, cel puțin în majoritatea scopurilor.
Poate că o definiție utilă a exponenților pentru matematicianul amator este următoarea: